Площадь криволинейной трапеции. Занятие № 36

1.

2.

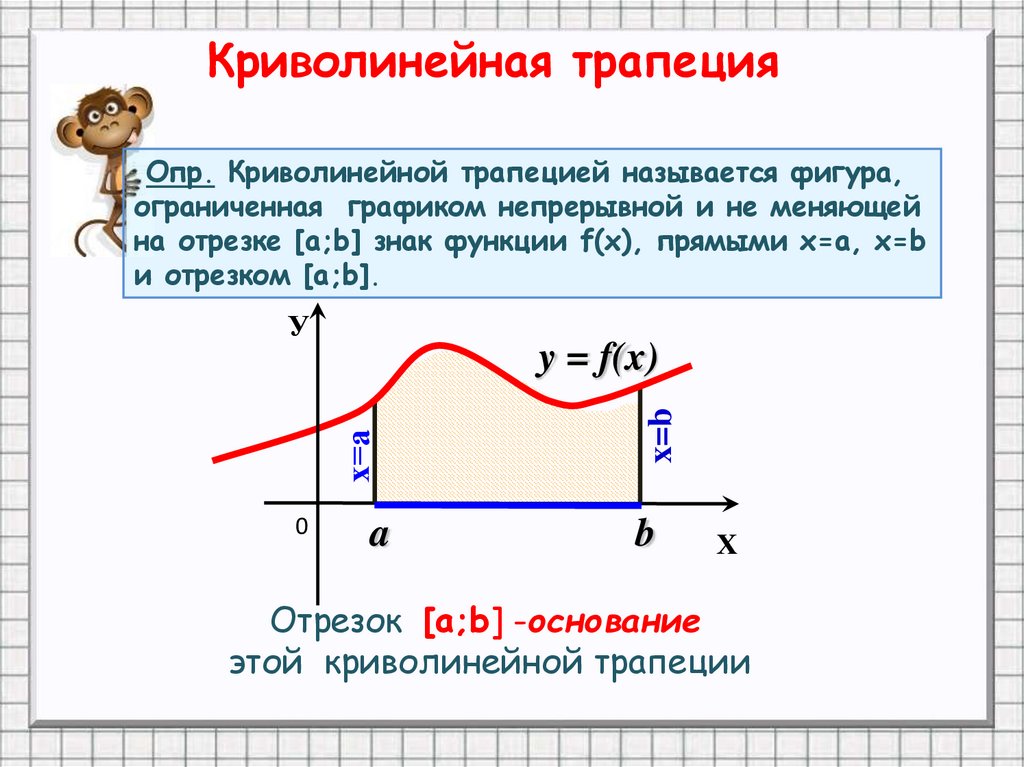
Криволинейная трапеция
Опр. Криволинейной трапецией называется фигура,
ограниченная графиком непрерывной и не меняющей
на отрезке [а;b] знак функции f(х), прямыми х=а, x=b
и отрезком [а;b].
У
0
a
x=b
х=а
y = f(x)
b
Х
Отрезок [a;b] -основание
этой криволинейной трапеции

3.

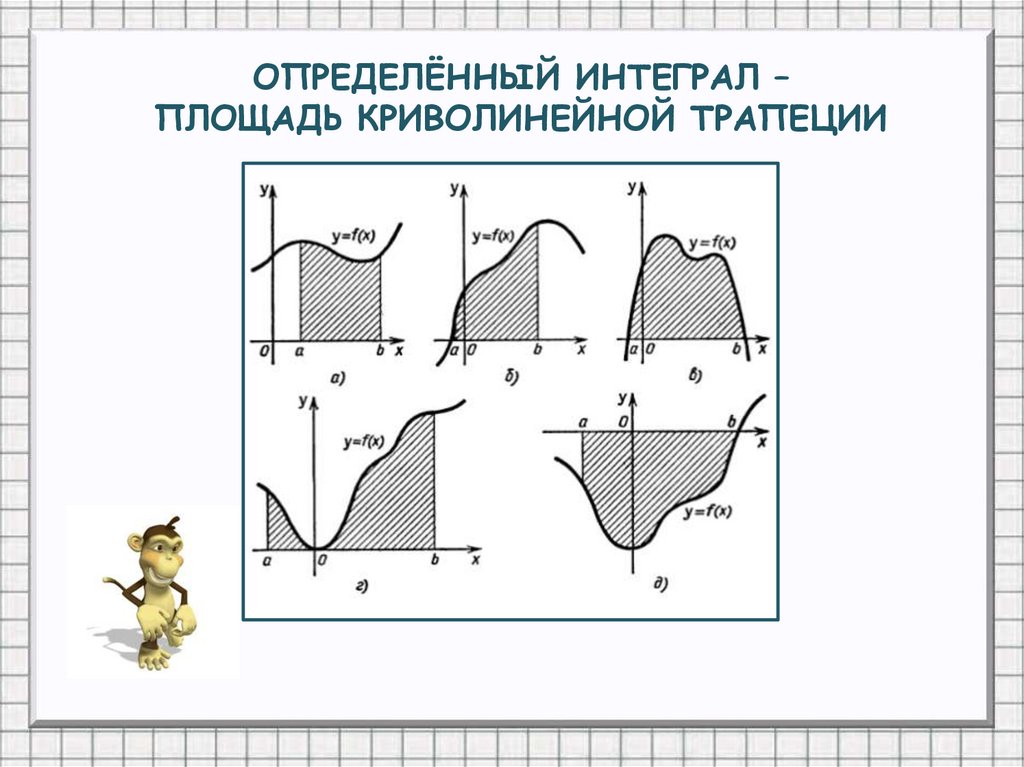
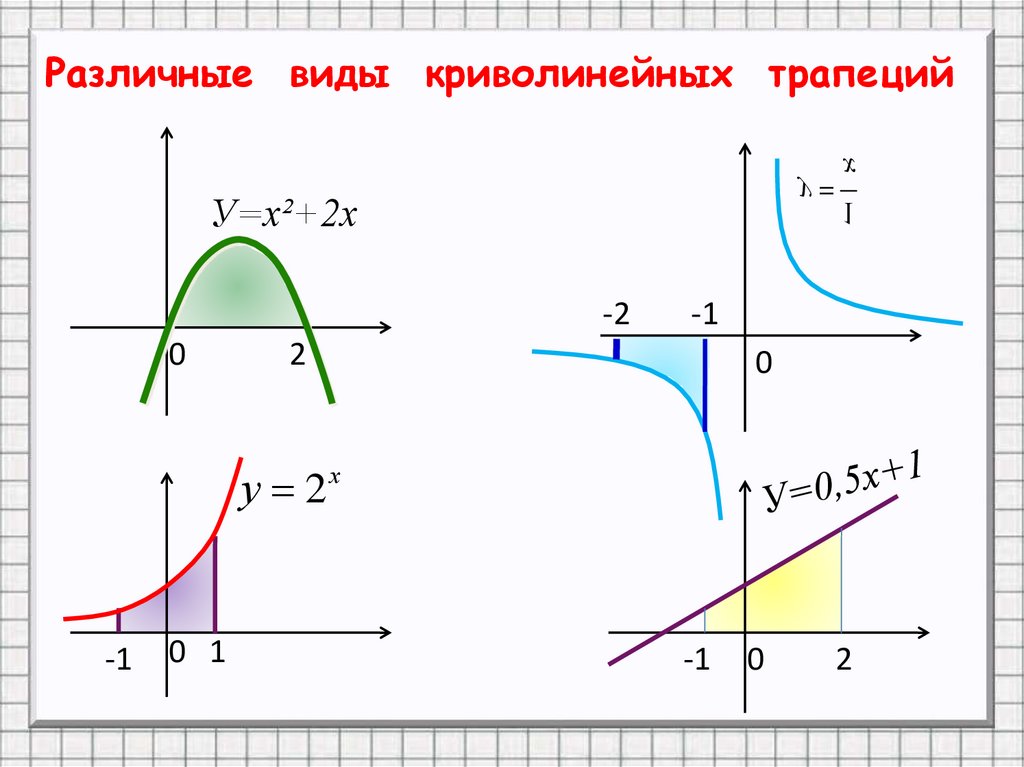
Различные виды криволинейных трапеций

4.

Формула Ньютона-Лейбница
И.Ньютон
1643—1727
Г.Лейбниц
1646—1716

5.

ОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ –
ПЛОЩАДЬ КРИВОЛИНЕЙНОЙ ТРАПЕЦИИ

6.

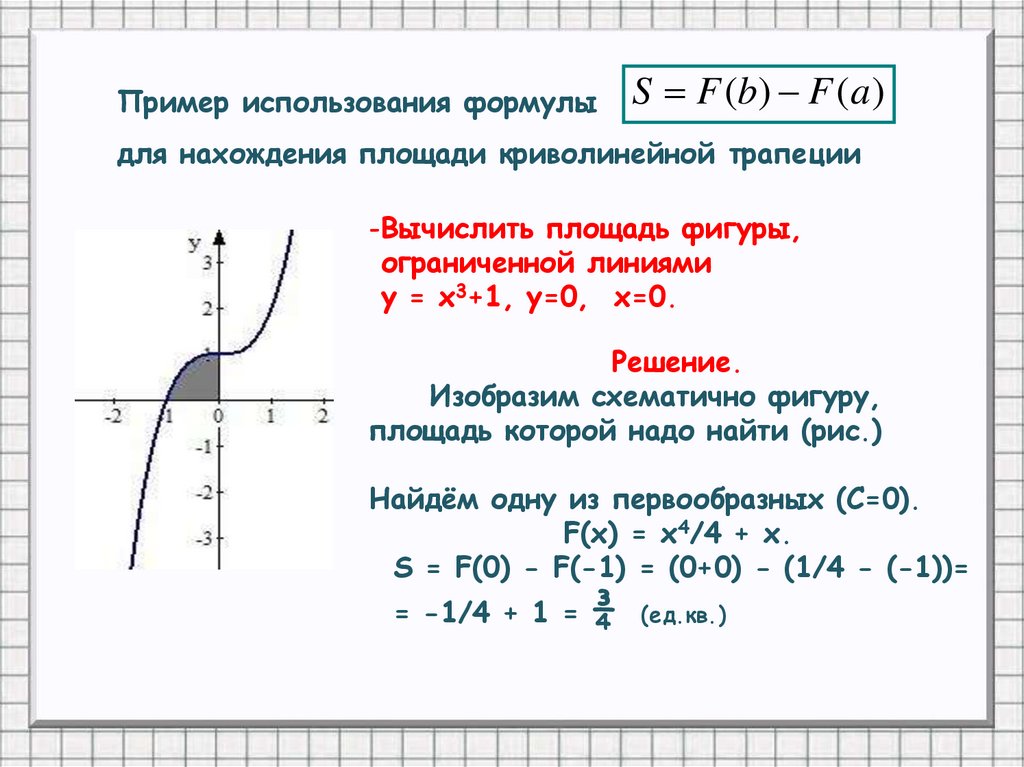
Пример использования формулы
S F (b) F (a )
для нахождения площади криволинейной трапеции
-Вычислить площадь фигуры,
ограниченной линиями
у = x3+1, у=0, x=0.
Решение.
Изобразим схематично фигуру,
площадь которой надо найти (рис.)
Найдём одну из первообразных (С=0).
F(x) = x4/4 + x.
S = F(0) - F(-1) = (0+0) - (1/4 - (-1))=
= -1/4 + 1 = ¾
(ед.кв.)

7.

8.

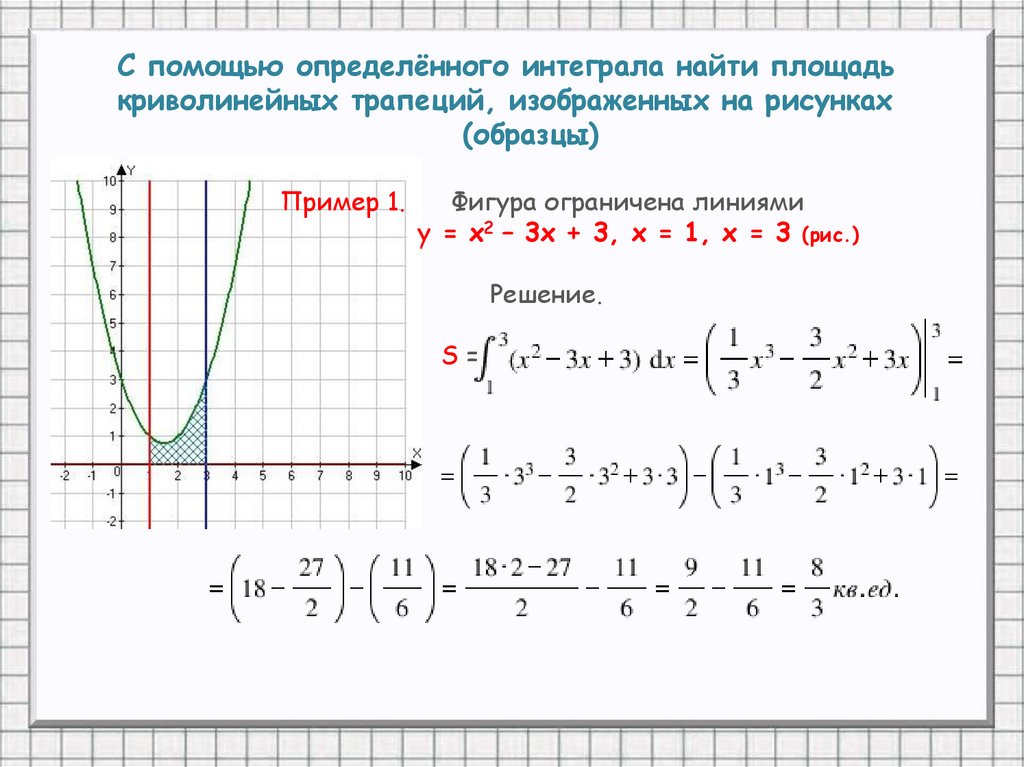
С помощью определённого интеграла найти площадь
криволинейных трапеций, изображенных на рисунках
(образцы)
Пример 1.
Фигура ограничена линиями
у = х2 – 3х + 3, х = 1, х = 3 (рис.)
Решение.
S=

9.

Пример 2.
Фигура ограничена линиями
у = 1 – х2, х = -½, х = 1 , у = 0 (рис.)
Решение.
S=
(ед.кв.)
Пример 3.
Фигура ограничена линиями
у = sin x, x = π/2, осью Ох (рис.)
Решение.
S=
(ед.кв.)
0

10.

Различные виды криволинейных трапеций
х
у
1
У=х²+2х
-2
0
2
у 2
-1
0 1
-1
0
х
-1
0
2

11.

ТРЕНИНГ «От простого к сложному».
По готовым рисункам найти площади фигур.
(Вариант 1 – задания с нечётными номерами, Вариант 2 – с чётными)
1)
4)
2)
5)
3)
6)
Лист 1

12.

7)
10)
8)
9)
11)
12)
Лист 2

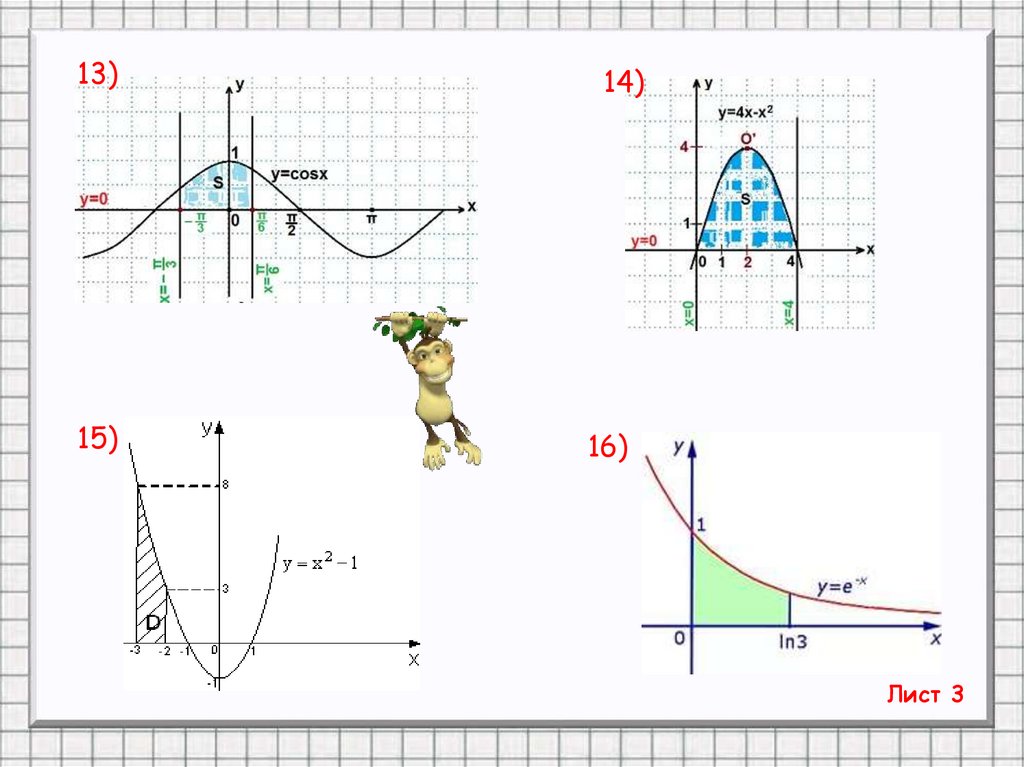
13.

13)
14)
15)
16)
Лист 3

14.

17)
20)
18)
21)
19)
22)
Лист 4

15.

23)
26)
24)
27)
25)
28)
Лист 5

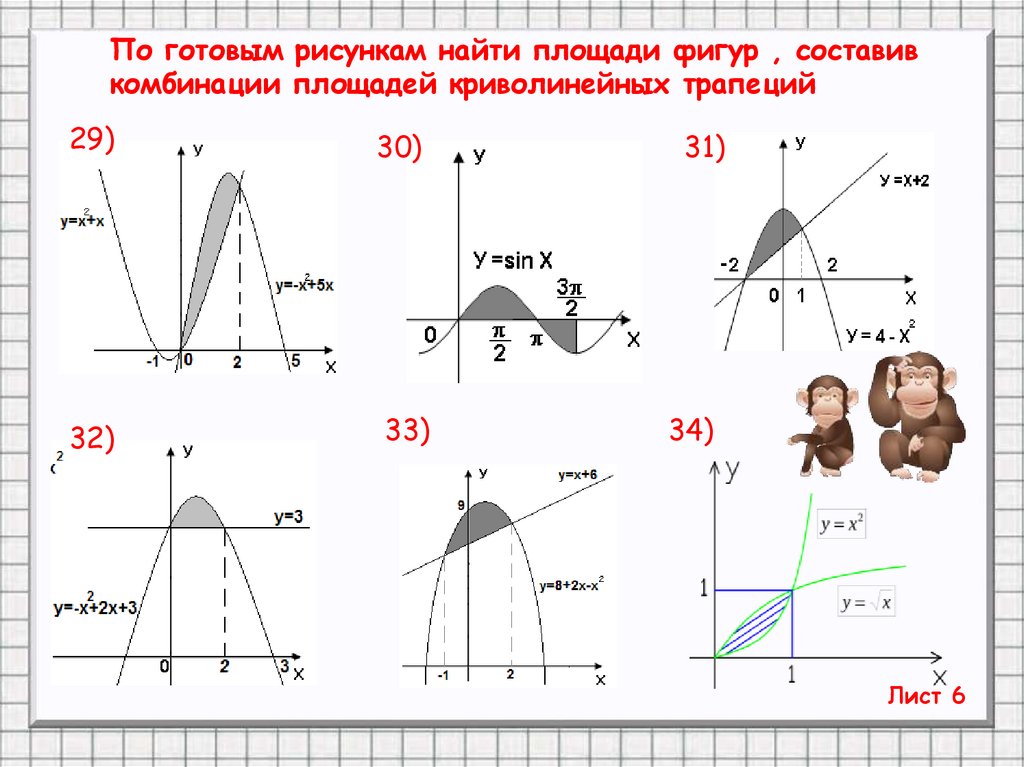
16.

По готовым рисункам найти площади фигур , составив
комбинации площадей криволинейных трапеций
29)
30)
31)
32)
33)
34)
Лист 6