Похожие презентации:
Линейное дифференциальное уравнение
1.
Линейное дифференциальное уравнениеa0 y
(n)
a1 y
( n 1)
... an 1 y ' an y f ( x)
при f(x) ≡ 0 – однородное уравнение, при f(x) ≠ 0 – неоднородное.
Общее решение неоднородного линейного уравнения – сумма
общего решения однородного уравнения и произвольного
частного решения неоднородного.
Общее решение однородного уравнения имеет n корней:
где С1, Сn – произвольные постоянные.
2.
В случае, если коэффициенты ai действительны и постоянны (вобщем случае это могут быть a(х)), ai=const, составляется и
решается характеристическое уравнение:
Уравнение n-го порядка имеет n корней.
Получим решение однородного уравнения:
В случае кратных корней слагаемых будет меньше, но
некоторые Ci станут полиномами…
При наличии комплексных корней будут сопряженные пары
λ=α+iβ и λ= α–iβ, соответствующие им
e
( i ) x
следует заменить на
e x cos( x)
и
e x sin( x)
3.
Пример 1y ' ' ' y 0
характеристическое уравнение:
1 0
3
решаем……..
4.
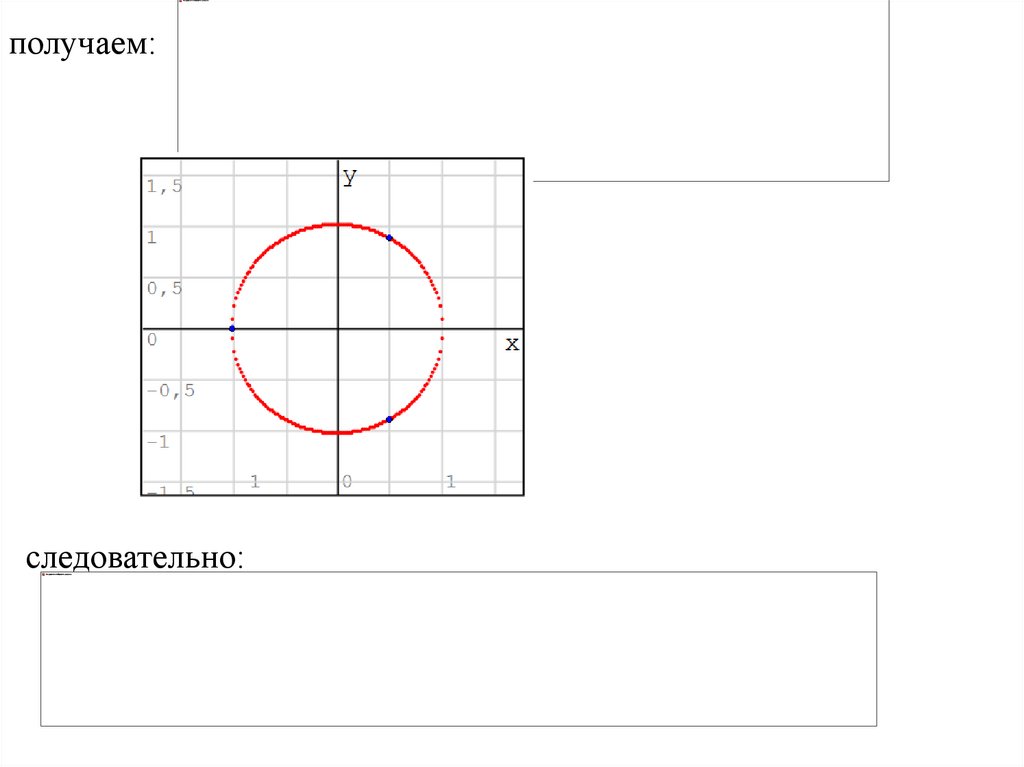
получаем:следовательно:
5.
Поиск частного решения.1.
f ( x) e Pm ( x)
ax
где Pm – многочлен степени m, частное решение нужно искать в
виде:
где s=0 если a – не корень характеристического уравнения, а
если корень, то s – кратность этого корня.
Qm – многочлен, коэффициенты которого определяются
подстановкой полученного yЧ в исходное дифф уравнение.
6.
2.частное решение нужно искать в виде:
где s=0 если a – не корень характеристического уравнения, а
если корень, то s – кратность этого корня; m – max(m1,m2).
3.
Если правая часть – сумма функций, то частное решение
нужно искать в виде суммы частных решений для каждой
функции.
7.
Пример 2решаем……..
8.
получаем:9.
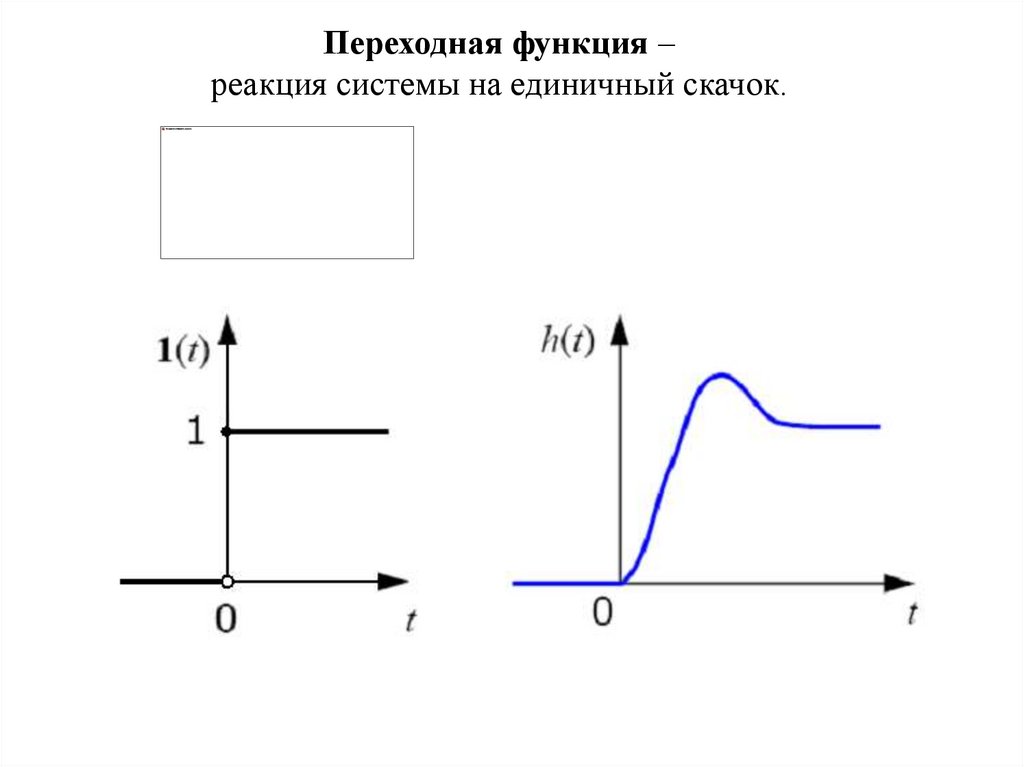
Переходная функция –реакция системы на единичный скачок.
10.
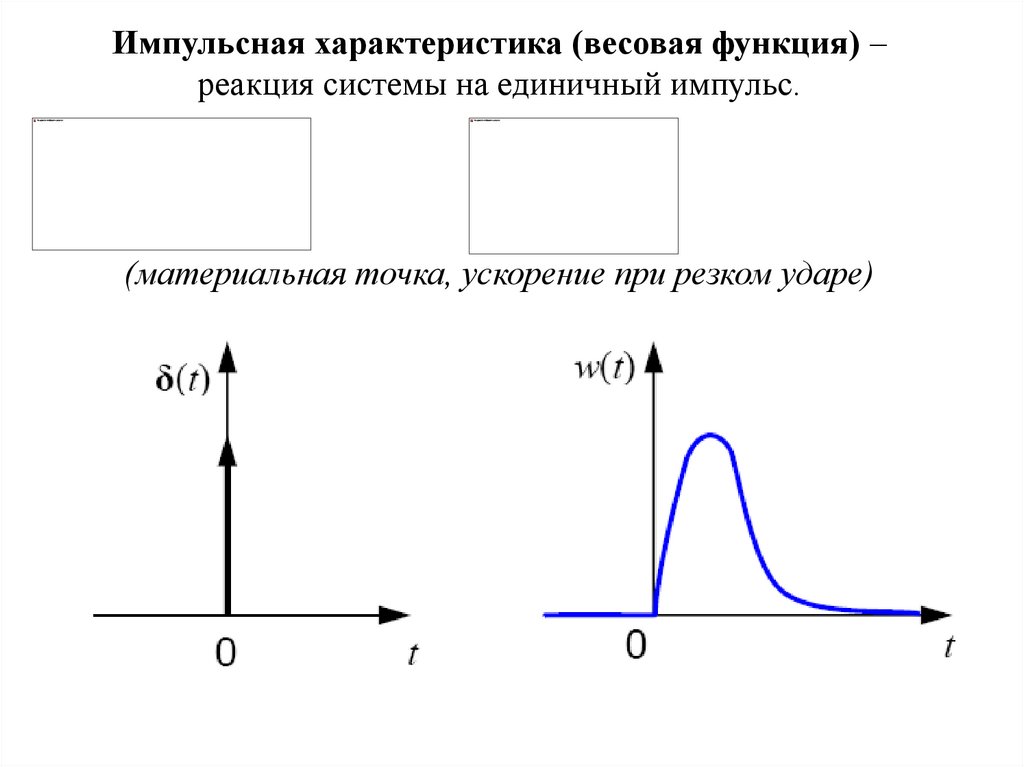
Импульсная характеристика (весовая функция) –реакция системы на единичный импульс.
(материальная точка, ускорение при резком ударе)
11.
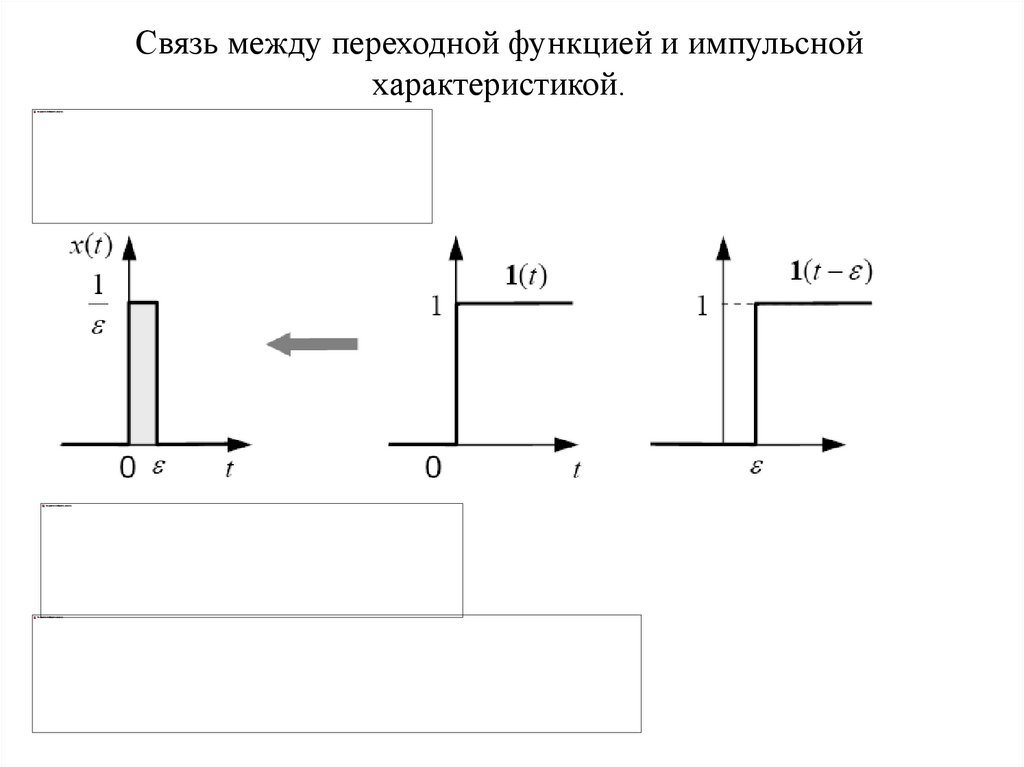
Связь между переходной функцией и импульснойхарактеристикой.
12.
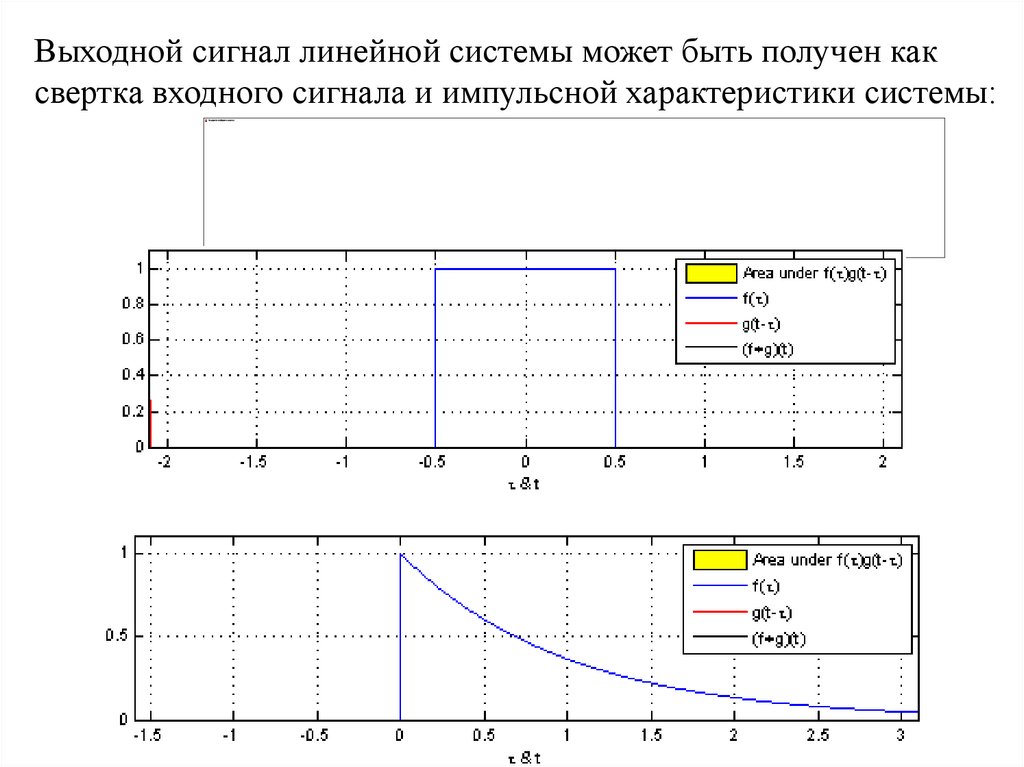
Выходной сигнал линейной системы может быть получен каксвертка входного сигнала и импульсной характеристики системы:
13.
Передаточная функцияПусть вход x(t) и выход y(t) связывает линейное ДУ 2-го порядка:
Оператор дифференцирования:
d
p
dt
14.
Оператор W(p) – передаточная функция, описывает связьмежду выходом и входом при нулевых начальных условиях.
p
Передаточная функция:
• правильная, если степень ее числителя не
p 1
больше, чем степень знаменателя;
1
• строго правильная, если степень числителя
p 1
меньше степени знаменателя;
• неправильная, если степень числителя
p2 p 1
больше, чем степень знаменателя.
p 1
Нули передаточной функции – корни числителя,
полюса – корни знаменателя.
p 1
имеет нуль в точке р = 1,
p 2 3 p 2 и полюса в точках р= –1 и р= –2 .
15.
Определить переходную и весовую функции следующих звеньевдвумя способами – решением ДУ и операторным:
1) Апериодического звена Ty’ + y = kx
2) Апериодического неустойчивого звена Ty’ – y = kx
3) Интегрирующего звена Ty’ = kx
4) Дифференцирующего звена y = Тx’
5) Форсирующего звена первого порядка y = k(x + Tx’)
6) Реального дифференцирующего звена Ty’ + y = kx’
16.
Ответы:1) Апериодического звена h(t) = k(1 – e–t/T), w(t) = (k/T)*(e–t/T)
2) Апериодического неустойчивого звена h(t) = k(et/T – 1) , w(t) =
(k/T)*(et/T)
3) Интегрирующего звена h(t) = kt/T, w(t) = (k/T)*1(t)
4) Дифференцирующего звена h(t) = T*δ(t), w(t) = Tδ’(t)
5) Форсирующего звена первого порядка h(t) = k{1(t) + Tδ(t)},
w(t) = k{δ(t) + Tδ’(t)}
6) Реального дифференцирующего звена h(t) = k/T(e–t/T),
w(t) = (k/T2)*e–t/T) }









 Математика
Математика








