Похожие презентации:
Сумма углов треугольника
1.
Сумма углов треугольника2. … Да, путь познания не гладок. Но знаем мы со школьных лет, Загадок больше, чем разгадок, И поиска предела нет. Пифагор.
3. Сумма углов треугольника («метод ножниц»):
21. Разрежем данный треугольник
произвольными линиями:
1
2
2. Получим три угла:
3
1
3. Получившиеся три угла
образуют развернутый угол,
равный 180°
3
4.
Цели урока:Выдвинуть гипотезу о сумме углов
треугольника.
Сформулировать и доказать теорему о сумме
углов треугольника.
Научиться решать задачи используя данную
теорему.
5.
Может ли быть в треугольникедва прямых угла?
Может ли быть в треугольнике
два тупых угла?
Может ли быть в треугольнике
прямой и тупой углы?
6.
Теорема:Сумма углов треугольника равна 180°.
B
5
1
A
2
а
4
Дано: ▲АВС.
Доказать: А+ В+ С=180°
Доказательство:
3
C
1. Через вершину В проведем прямую а || AC.
2. И обозначим получившиеся углы.
3. 5= 1 и 4= 3 (1) – как накрест лежащие углы
4. 5+ 2+ 4=180° т.к. В - развернутый
5.Учитывая равенство (1), получаем 1+ 2+ 3=180°, или
А+ В+ С=180°
Теорема доказана.
7.
Первое доказательство было даноеще Пифагором (5 в. до н.э.)
В первой книге «Начала» Евклид
излагает другое доказательство
теоремы о сумме углов треугольника.
8.
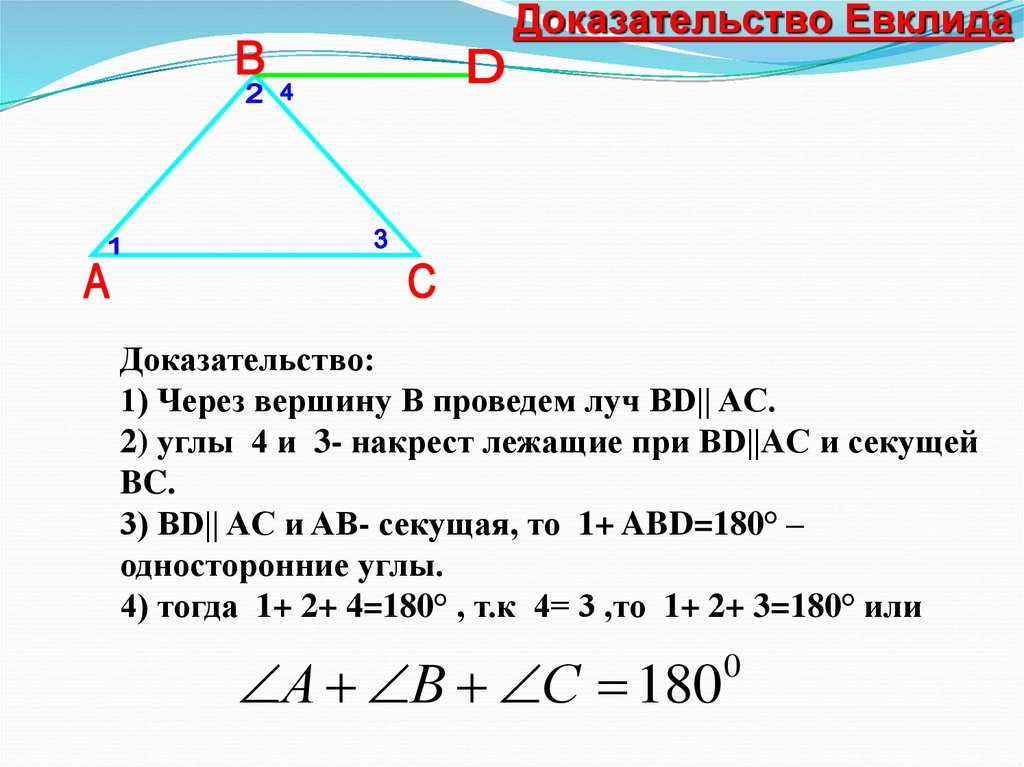
Доказательство ЕвклидаДоказательство:
1) Через вершину B проведем луч BD|| AC.
2) углы 4 и 3- накрест лежащие при BD||AC и секущей
BC.
3) BD|| AC и AB- секущая, то 1+ ABD=180° –
односторонние углы.
4) тогда 1+ 2+ 4=180° , т.к 4= 3 ,то 1+ 2+ 3=180° или
А В С 180
0
9.
DДано: ΔCDE,
DK- биссектриса
CDK=28°, CKD=75°
Найти: углы CDE
28°
75°
C
E
K
10.
№ 19(2)В
Дано: ΔАВС,
А: В: С =2:3:4
Найти: А, В, С
А
С
11.
Домашняя работа:3 способ доказательства:
B
E
2
A
1
3
4
5
C
П.33 №19(2), 22(2,3). Доказать теорему о сумме
углов треугольника, используя чертеж учеников
Пифагора.
12.
После изучения темы: «Сумма угловтреугольника» могу сказать…
Сегодня на уроке я испытал …
Геометрия мой любимый предмет и …
Геометрия не мой любимый предмет, но …
Быть проницательным …











 Математика
Математика








