Л-2_Предел переменной величины

1.

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
«ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ МОРСКОГО И РЕЧНОГО ФЛОТА ИМЕНИ АДМИРАЛА С.О. МАКАРОВА»
Предел
переменной
величины
Доцент кафедры
высшей математики
Елена Ивановна Распутина

2.

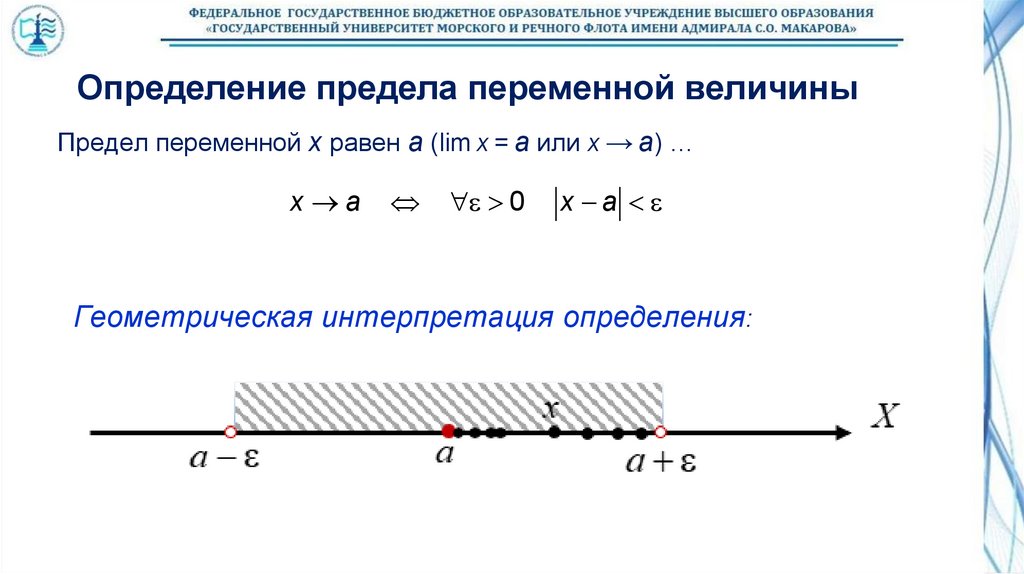
Определение предела переменной величины
Предел переменной x равен a (lim x = a или x → a) …
x a
0
x a
Геометрическая интерпретация определения:

3.

Определение. Бесконечно малая величина — величина предел,
которой равен нулю
— б/м
0
0
Здесь «0» — символ бесконечно малой величины.
Определение. Бесконечно большая величина — величина предел,
которой равен бесконечности
X — б/б
x
M 0
x M
Здесь «∞» — символ бесконечно большой величины
Замечание. Для зависимой переменной
указывается, как изменяется аргумент.
f x А;
x x0
lim f x ;
x x0
lim f x ;
x
под
символом
lim an lim f n .
n
n
предела

4.

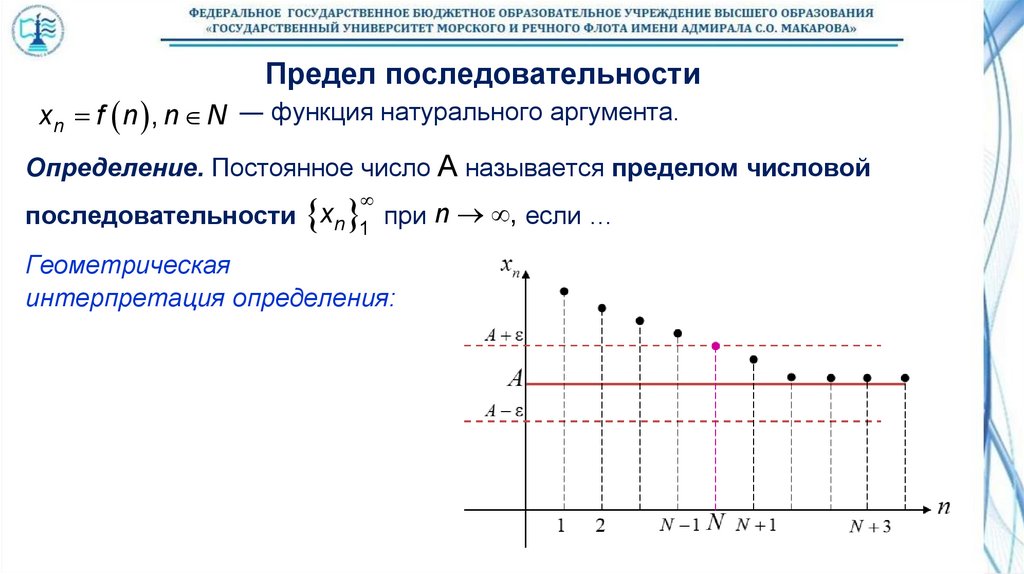
Предел последовательности
xn f n , n N ― функция натурального аргумента.
Определение. Постоянное число A называется пределом числовой
последовательности
xn 1 при n , если …
Геометрическая
интерпретация определения:

5.

Предел последовательности
Определение предела последовательности в логических
символах:
lim xn A 0 N N :
n
n N xn A

6.

Последовательность
сходящийся, если она имеет
конечный предел:
lim xn lim f n A или
n
n
lim xn 0
n
xn 1 называется
расходящийся, если никакое
число не является ее пределом:
lim xn
n
lim xn не существует
n
Например,
n 1
lim
1
n n
1
lim 0
n n
lim xn lim 2n 2
n
n
lim 1
n
n

7.

Предел функции
y = f (x) ― функция непрерывного аргумента
Определение. Число А называется пределом функции y = f (x) в точке x0
(или при x → x0), если …
Определение предела функции в логических символах, на языке δ-ε:
lim f x A 0 :
x x0
x x0 , x x0 f x A

8.

Например,
Первый замечательный предел
sin x
lim
1
x 0 x
Предел константы
lim const const
x x0
x
lim x x0
x x0

9.

Геометрическая интерпретация определения предела функции в
точке:

10.

Бесконечно малые и бесконечно большие функции
Определение. Функция x — б/м, если …
lim x 0
x x0
Cвязь между функцией, ее пределом и бесконечно малой функцией
Теорема о функции, которая имеет конечный предел
lim f x A f x A x , x 0
x x0
x x0

11.

Свойства бесконечно малых функций
lim x 0,
x x0
lim x 0
x x0
1) Предел суммы конечного числа бесконечно малых функций
lim x x 0
x x0
2) Предел произведения ограниченной функции и бесконечно малой функции
lim f x x 0, где f x M ― ограниченная функция.
x x0

12.

Упражнение.
sin x
а) lim
0
2
x x 1
cos n
0
б) lim
n
n 2
Связь между бесконечно большими и бесконечно малыми
Теорема о связи между б/м и б/б величинами
lim f x
x x0
lim α x 0
x x0
1
lim
0
x x0 f x
1
lim
x x0 α x

13.

ВЫЧИСЛЕНИЕ ПРЕДЕЛОВ
1) Предел функции f (x) в точке непрерывности x0 равен значению
функции в этой точке
lim f x f x0 , f (x) ― непрерывна в точке x0.
x x0
2) Символ предела и функциональной зависимости можно менять
местами для непрерывных функций
lim f g x f lim g x , f (x) ― непрерывная функция.
x x0
x x0
x
x

14.

3) Теорема об арифметических действиях с пределами.
Если lim f x A и lim g x B, то их сумма, разность, произведение и
x x0
x
x x0
x
(при условии
) частное имеют конечные пределы, причем
lim f x g x lim f x lim g x A B
x x0
x
x x0
x
x x0
x
lim f x g x lim f x lim g x A B
x x0
x
x x0
x
x x0
x

15.

3) Теорема об арифметических действиях с пределами
lim f x
x x0
x
f x
A
lim
x x0
g x
lim g x 0 B
x x
x
0
x
lim const f x const lim f x const A
x x0
x
x x0
x

16.

Упражнение. Вычислить
а) lim x 3 2 x 2 1
x 2
x2 1 1 1
б) lim
0
x 1 3 5 x
3 5
в) lim n 2 n 1 5
n