Дифференциальное исчисление функций одной действительной переменной

1. Дифференциальное исчисление функций одной действительной переменной

12. Касательная прямая.
Геометрический смысл
производной и дифференциала

2.

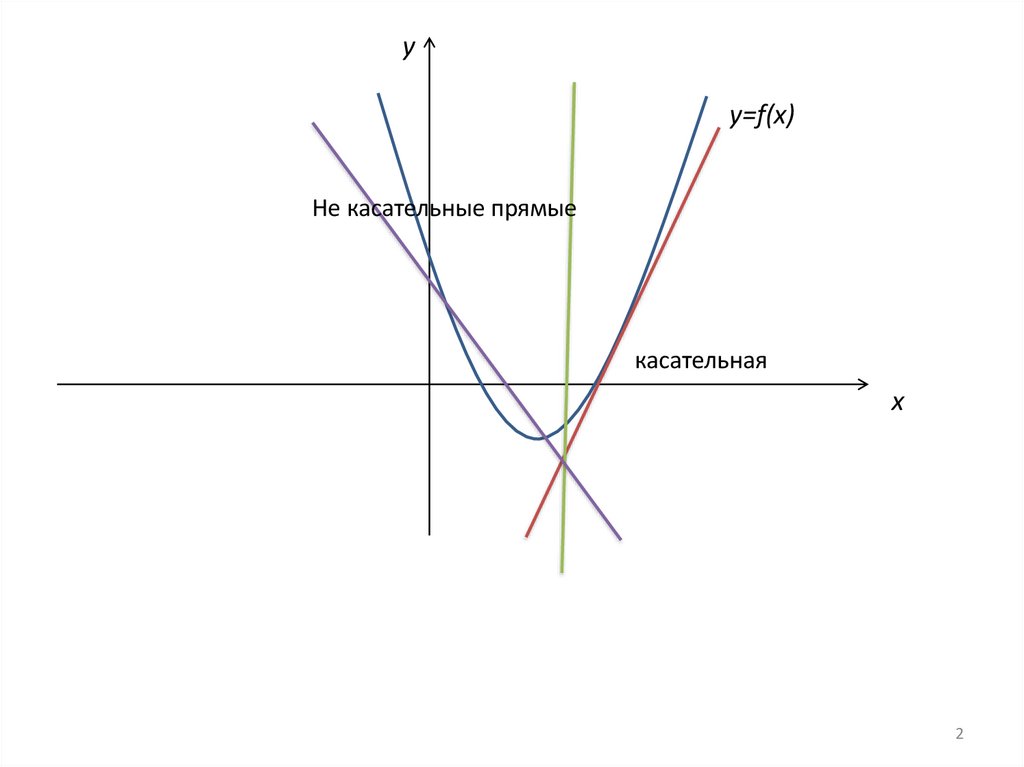
у
у=f(х)
Не касательные прямые
касательная
х
2

3. Касательная прямая

Могут ли данные предложения являться определениями касательной прямой к графику
функции?
Касательная прямая ?
• Касательной к графику функции y=f(x) в
точке (х0; f(x0)) называют прямую, проходящую
через точку (х0; f(x0)), с отрезком которой
практически сливается график функции при
значениях х сколь угодно близких к х0.
• - прямая, проходящая через точку кривой и
совпадающая с ней в этой точке с точностью до
первого порядка.
• - прямая, имеющая одну общую точку с графиком
функции.
• - прямая, график функции относительно которой
располагается с одной стороны.
• - прямая, с которою стремится совпасть секущая,
проведенная через две точки на произвольной
кривой по мере сближения этих точек.
3

4. Касательная прямая

• Касательной к графику функции y=f(x) в
точке (х0; f(x0)) называют прямую, проходящую
через точку (х0; f(x0)), с отрезком которой
практически сливается график функции при
?
значениях х сколь угодно близких к х0.
• - прямая, проходящая через точку кривой и
совпадающая с ней в этой точке с точностью до ?
первого порядка.
• - прямая, имеющая одну общую точку с графиком
функции.
• - прямая, график функции относительно которой
располагается с одной стороны.
• - прямая, с которою стремится совпасть секущая,
?
проведенная через две точки на произвольной
кривой по мере сближения этих точек.
4

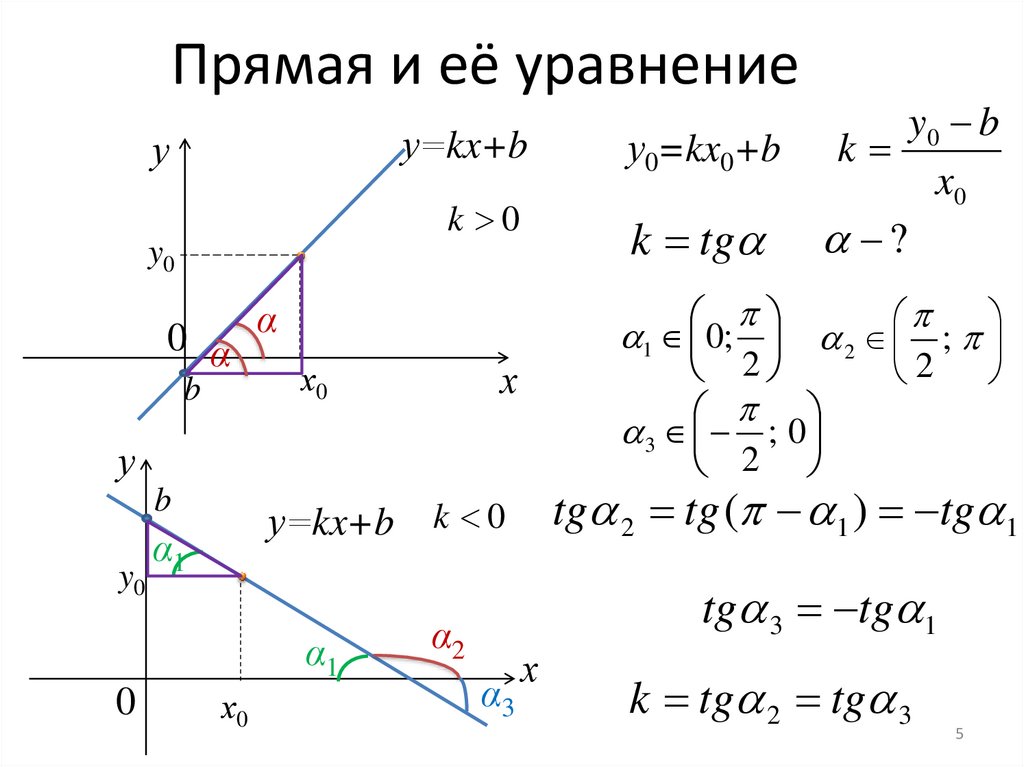
5. Прямая и её уравнение

у=kx+b
у
k 0
y0
0 α
b
1 0; 2 ;
2
2
3 ; 0
2
α
х
х0
у
b
y0
α1
0
tg 2 tg ( 1 ) tg 1
у=kx+b k 0
α1
х0
y0 b
у0=kx0+b k
x0
k tg ?
tg 3 tg 1
α2
α3
х
k tg 2 tg 3
5

6.

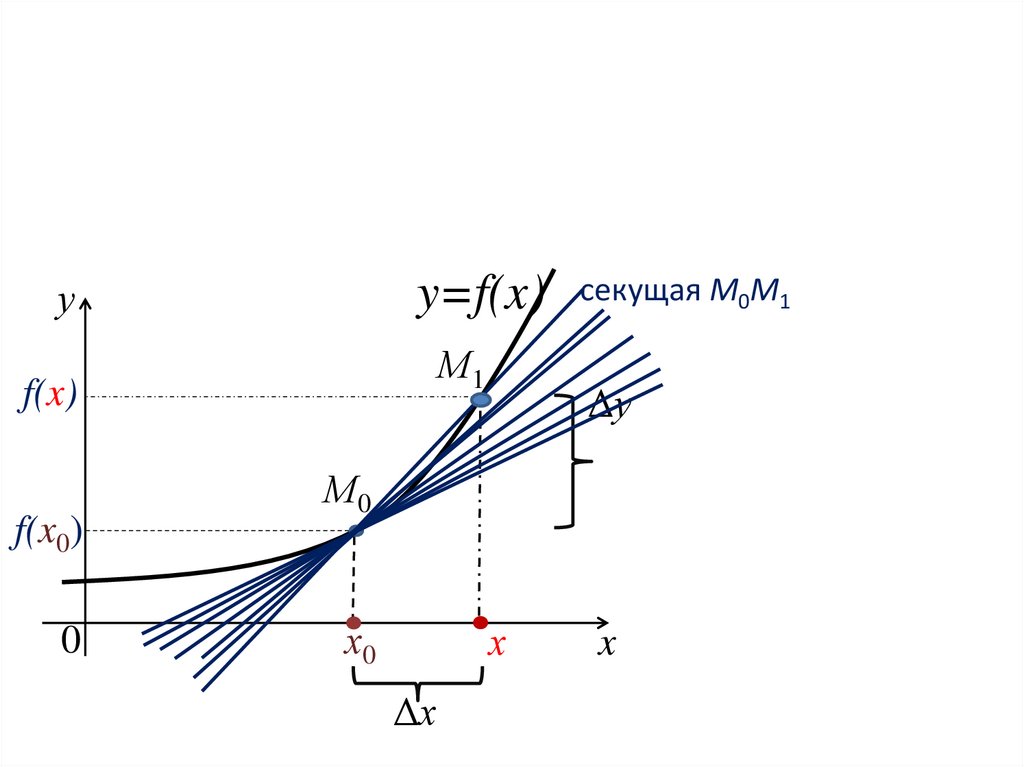
y=f(x) секущая М0М1
у
М1
f(x)
f(x0)
0
Δу
М0
х0
х
Δх
x

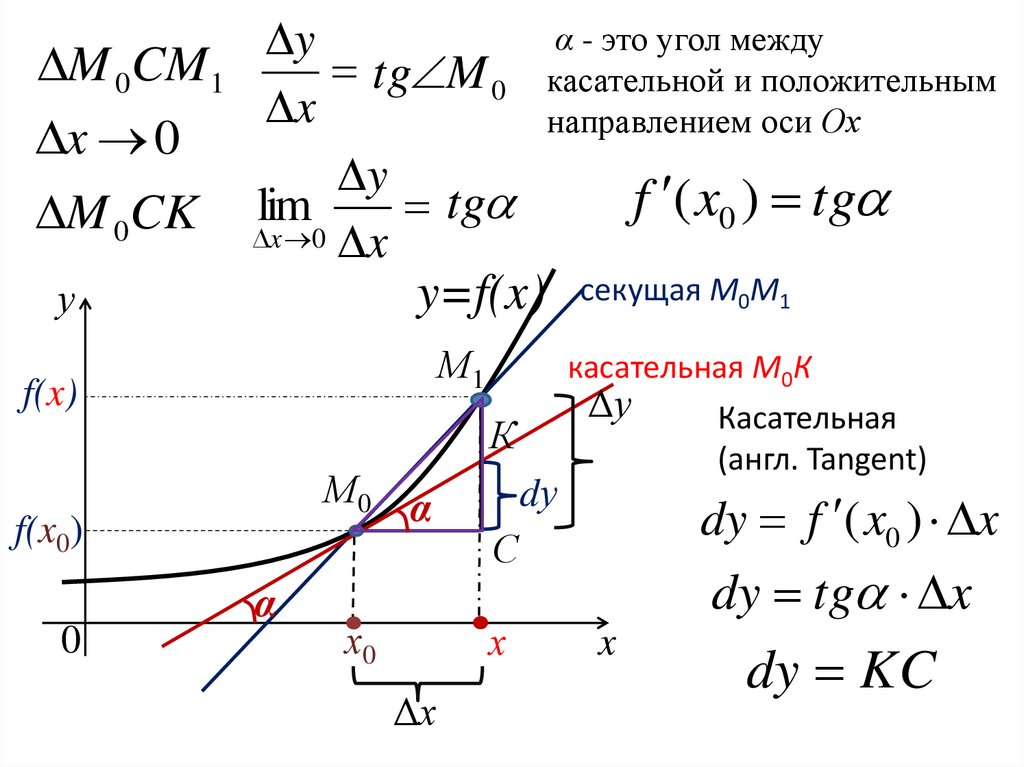
7.

α - это угол между
y
M 0CM1
tg M 0 касательной и положительным
x
направлением оси Ох
x 0
y
f ( x0 ) tg
tg
M 0CK lim
x 0 x
y=f(x) секущая М0М1
у
М1
f(x)
К
f(x0)
α
0
М0 α
dу
С
х0
х
Δх
касательная М0К
Δу
Касательная
(англ. Tangent)
dy f ( x0 ) x
dy tg x
x
dy KC

8. Касательная прямая

• Касательной прямой к графику функции у=f(x)
в точке М0(х0; f(x0)) называется прямая
являющаяся предельным положением секущих
(прямых М0М1), при условии, что точка М1
(х0+∆х; f(x0 +∆х)) приближается, двигаясь по
графику функции у=f(x), к точке касания М0.
• Геометрический смысл производной:
производная функции у=f(x) в точке x0 равна
угловому коэффициенту касательной,
проведенной к графику данной функции в
точке с абсциссой x0, т.е. f ( x0 ) tg
8

9.

• Геометрический смысл дифференциала:
дифференциал функции у=f(x) в точке x0 равен
приращению ординаты касательной к графику
данной функции в точке, абсцисса которой равна
x0, когда х получит приращение ∆x.
у
М1
f(x)
f(x0)+dy
f(x0)
0
y=f(x)
К
М0 α
х0 Δх
Δу
dу
С
х
dy f ( x0 ) x
dy tg x
dy KC
x
x 0
y dy
9

10. Приближенные вычисления с помощью дифференциала

y f ( x0 ) x o( x)
x 0
y df ( x0 ) o( x)
y df ( x0 )
f ( x0 x) f ( x0 ) f ( x0 ) x o( x)
f ( x0 x) f ( x0 ) f ( x0 ) x
f ( x0 x) f ( x0 ) f x ( x0 ) x
10

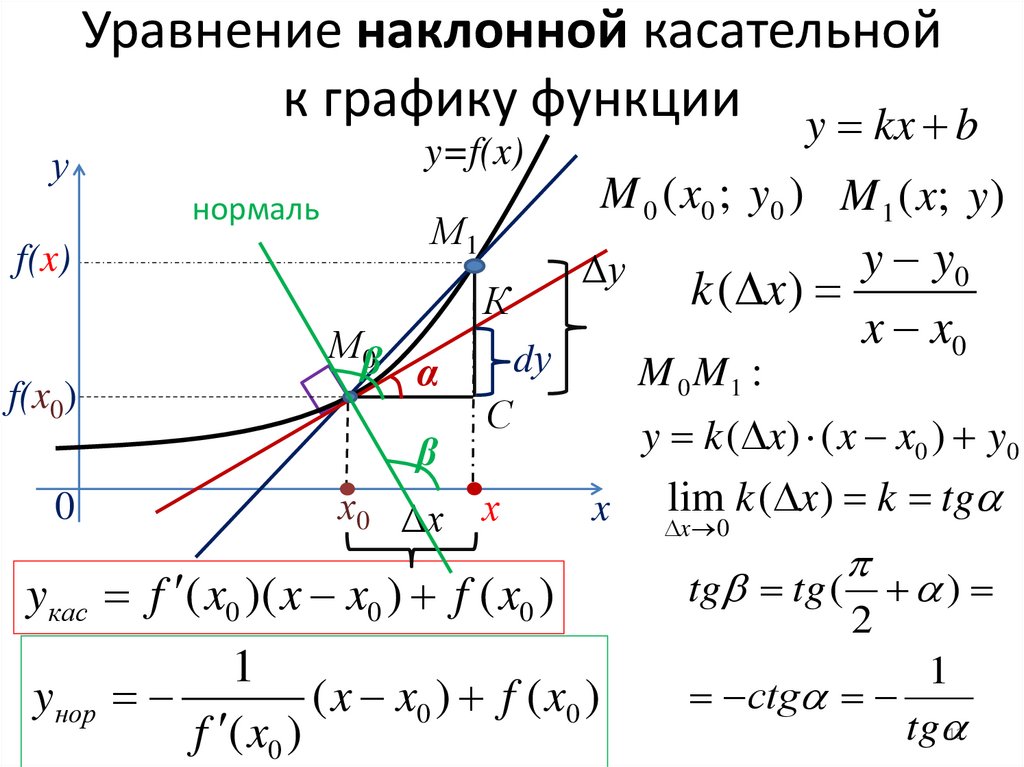
11. Уравнение наклонной касательной к графику функции

у
Уравнение наклонной касательной
к графику функции y kx b
y=f(x)
нормаль
f(x)
f(x0)
M 0 ( x0 ; y0 ) M 1 ( x; y )
М1
Мβ0
α
К
dу
С
Δу
y y0
k ( x)
x x0
M 0 M1 :
y k ( x) ( x x0 ) y0
k ( x) k tg
0
х0 Δх х
x lim
x 0
tg tg ( )
yкас f ( x0 )( x x0 ) f ( x0 )
2
1
1
сtg
yнор
( x x0 ) f ( x0 )
tg 11
f ( x0 )
β

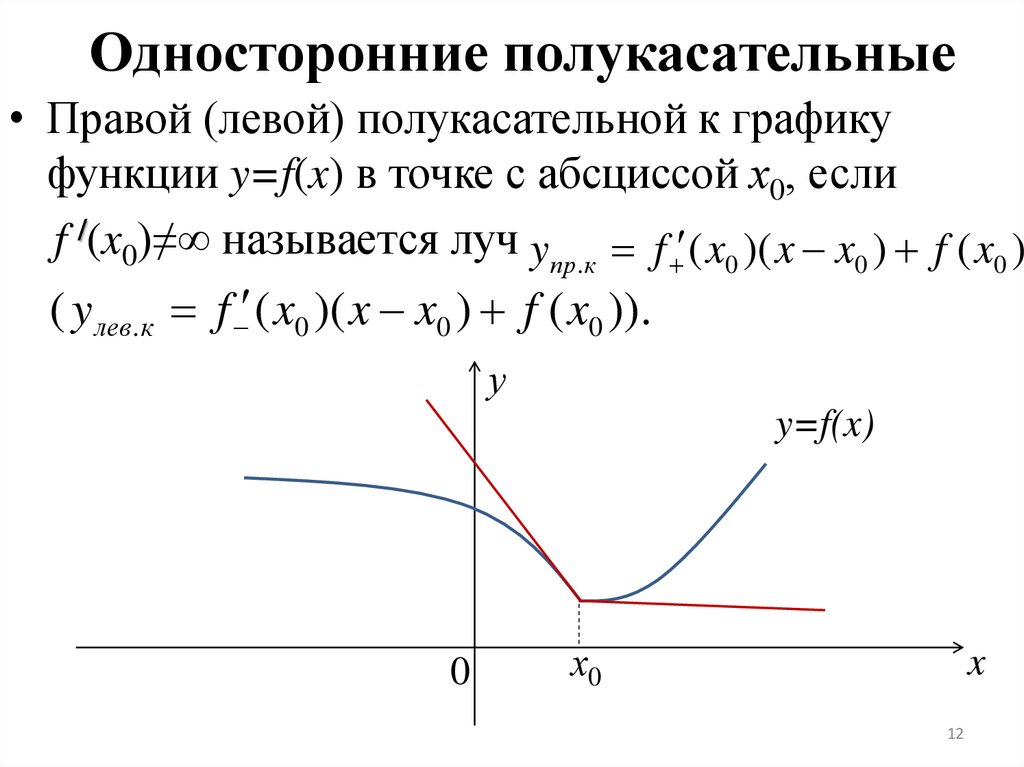
12. Односторонние полукасательные

• Правой (левой) полукасательной к графику
функции y=f(x) в точке с абсциссой х0, если
f /(x0)≠∞ называется луч yпр.к f ( x0 )( x x0 ) f ( x0 )
( y лев.к f ( x0 )( x x0 ) f ( x0 )).
у
y=f(x)
0
х0
x
12

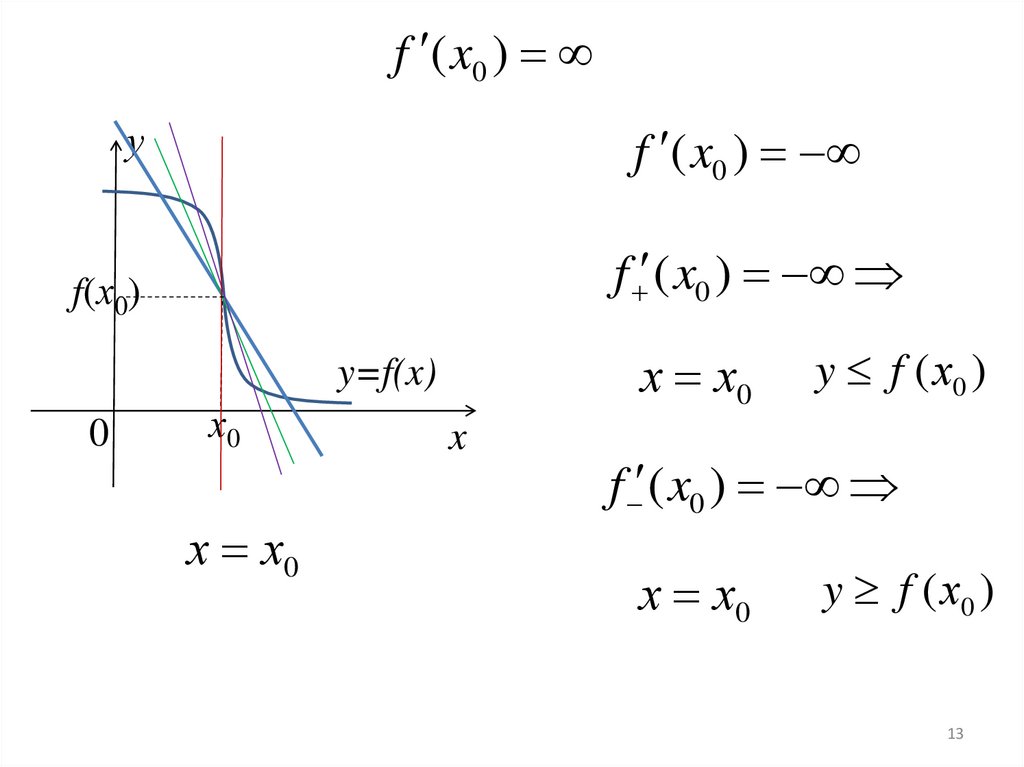
13.

f ( x0 )
f ( x0 )
у
f ( x0 )
f(х0)
х х0
y=f(x)
0
х0
х х0
x
y f ( х0 )
f ( x0 )
х х0
y f ( х0 )
13

14.

f ( x0 ) х х0 - уравнение касательной прямой
y f ( х0 ) - уравнение нормали
f ( x0 )
y f ( х0 )
f ( x0 )
y f ( х0 )
f ( x0 )
f ( x0 )
х х0
y f ( х0 )
- полукасательные
y f ( х0 )
14

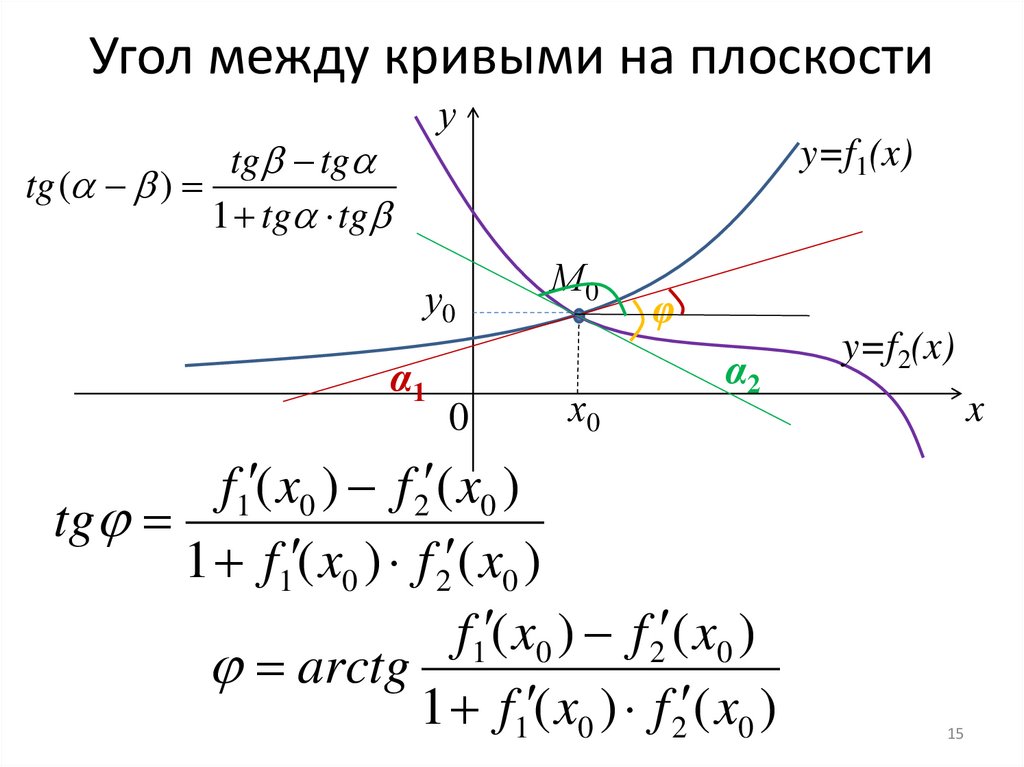
15. Угол между кривыми на плоскости

у
tg tg
tg ( )
1 tg tg
y=f1(x)
у0
α1
0
М0
х0
φ
α2
f1 ( x0 ) f 2 ( x0 )
tg
1 f1 ( x0 ) f 2 ( x0 )
f1 ( x0 ) f 2 ( x0 )
arctg
1 f1 ( x0 ) f 2 ( x0 )
y=f2(x)
x
15

16. Механический смысл производной

• Пусть материальная точка М движется
прямолинейно по закону S=S(t).
• Скорость прямолинейного движения
материальной точки в момент времени t есть
производная от пути S по времени t:
v S (t )
• Ускорение прямолинейного движения точки в
момент времени t есть вторая производная от
пути S по времени t:
a v (t ) S (t )
16

17. Физический смысл производной

• Если функция y=f(x) описывает какой-либо
физический процесс, то производная есть скорость
протекания этого процесса.
• Если Q=Q(t) – количество электричества,
проходящего через поперечное сечение проводника
за время t, то сила тока в момент времени t: I=Q/(t).
• Если m=m(x) – масса неоднородного стержня
между точками О(0; 0) и М(х; 0), то линейная
плотность стержня в точке х: S=m/(x).
• Если N=N(t) – количество вещества, вступившего в
химическую реакцию за время t, то скорость
химической реакции за время t: v=N/(t).
17