Дифференциальное исчисление функций одной действительной переменной

1. Дифференциальное исчисление функций одной действительной переменной

Раздел 2.
Дифференциальное исчисление
функций одной действительной
переменной
9. Дифференциал и производная
функции
Дифференциа́л (от лат. differentia – разность, различие)

2. Основатели теории ДИ

1671г. →1736г.
1684г.
Исаак Ньютон
Готфрид Вильгельм Лейбниц
Английский физик, математик, механик
и астроном, один из создателей
классической физики.
(04.01.1643 г. – 31.03.1727 г.)
Немецкий философ, логик, математик,
механик, физик, юрист, историк, дипломат,
изобретатель и языковед.
2
(01.07.1646 г. – 14 ноября 1716 г.)

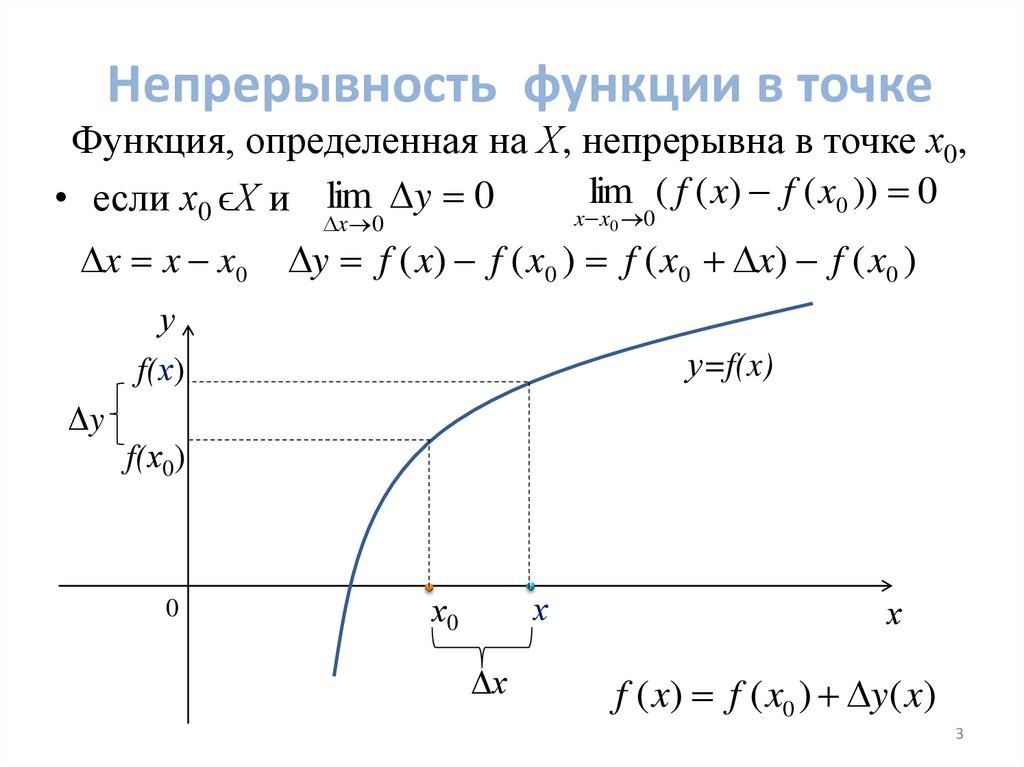
3. Непрерывность функции в точке

Функция, определенная на Х, непрерывна в точке х0,
lim ( f ( x) f ( x0 )) 0
• если х0 ϵХ и lim y 0
x x 0
x x x0
x 0
0
y f ( x) f ( x0 ) f ( x0 x) f ( x0 )
у
f(х)
у=f(x)
Δy
f(х0)
0
х
х0
Δх
х
f ( x) f ( x0 ) y( x)
3

4.

S
S
S=f(t)
S1
ΔS
ΔS
S0
0
S=f(t)
S1
S0
t1
t0
t
0
Δt
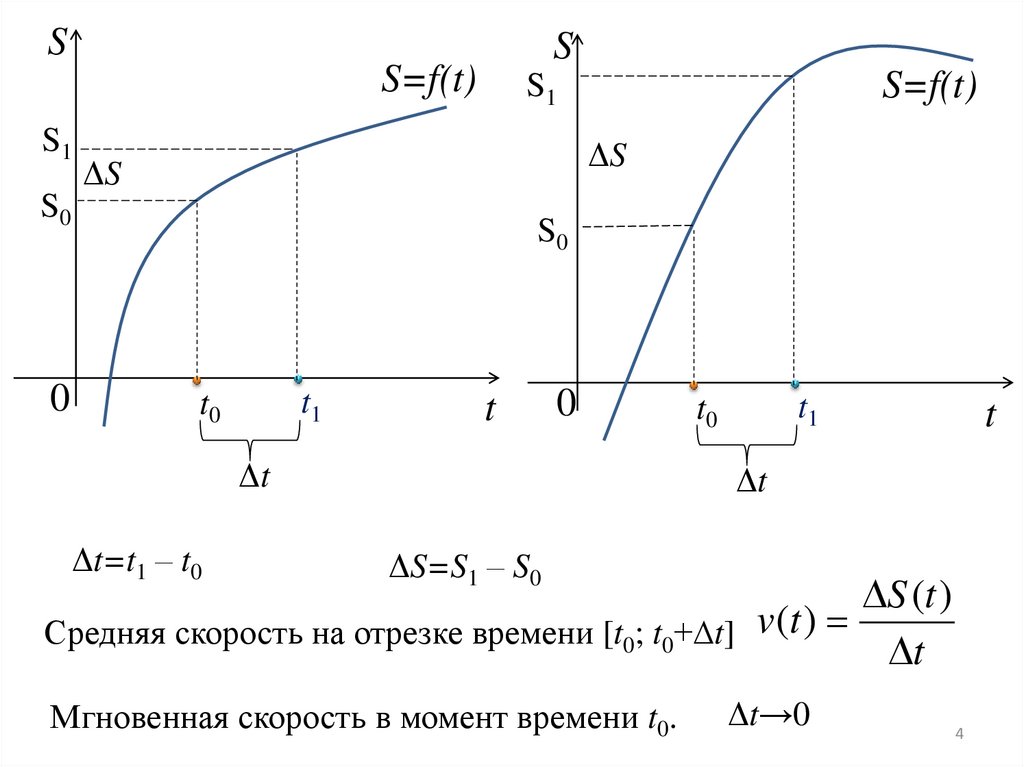
Δt=t1 – t0
t1
t0
t
Δt
ΔS=S1 – S0
S (t )
Средняя скорость на отрезке времени [t0; t0+∆t] v (t )
t
Мгновенная скорость в момент времени t0.
Δt→0
4

5.

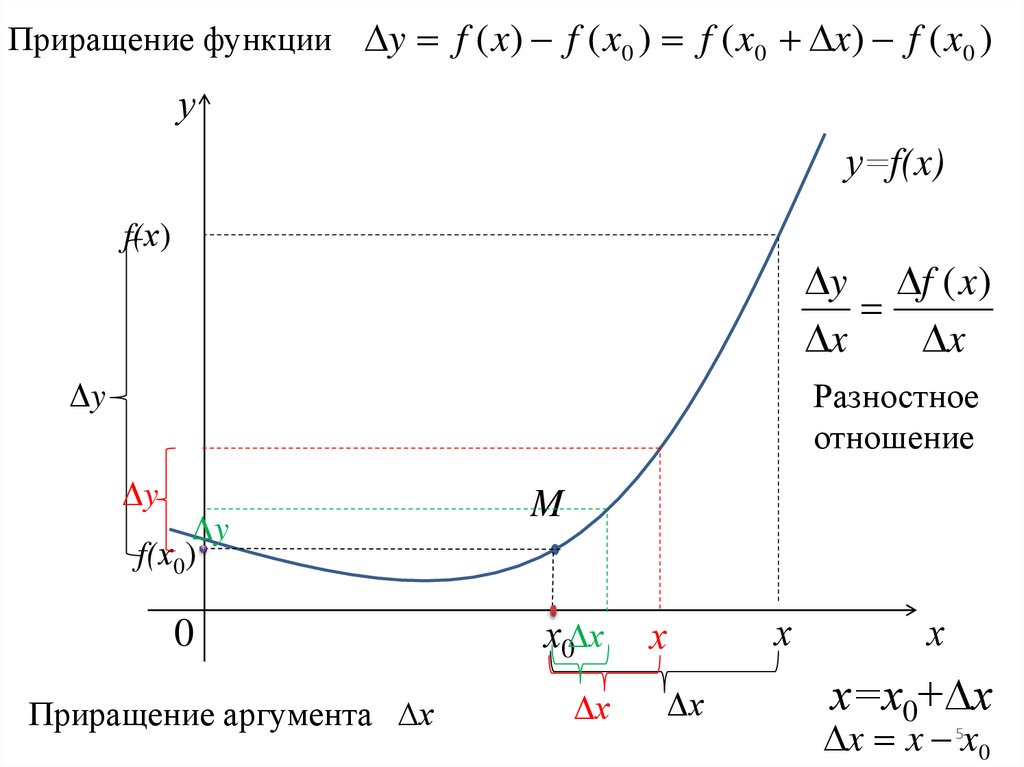
Приращение функции y f ( x) f ( x0 ) f ( x0 x) f ( x0 )
у
у=f(x)
f(х)
y f ( x)
x
x
Δy
Разностное
отношение
Δy
Δy
f(х0)
0
Приращение аргумента ∆х
M
х0Δх
Δх
х
Δх
х
х
х=х0+∆х
x x 5x0

6.

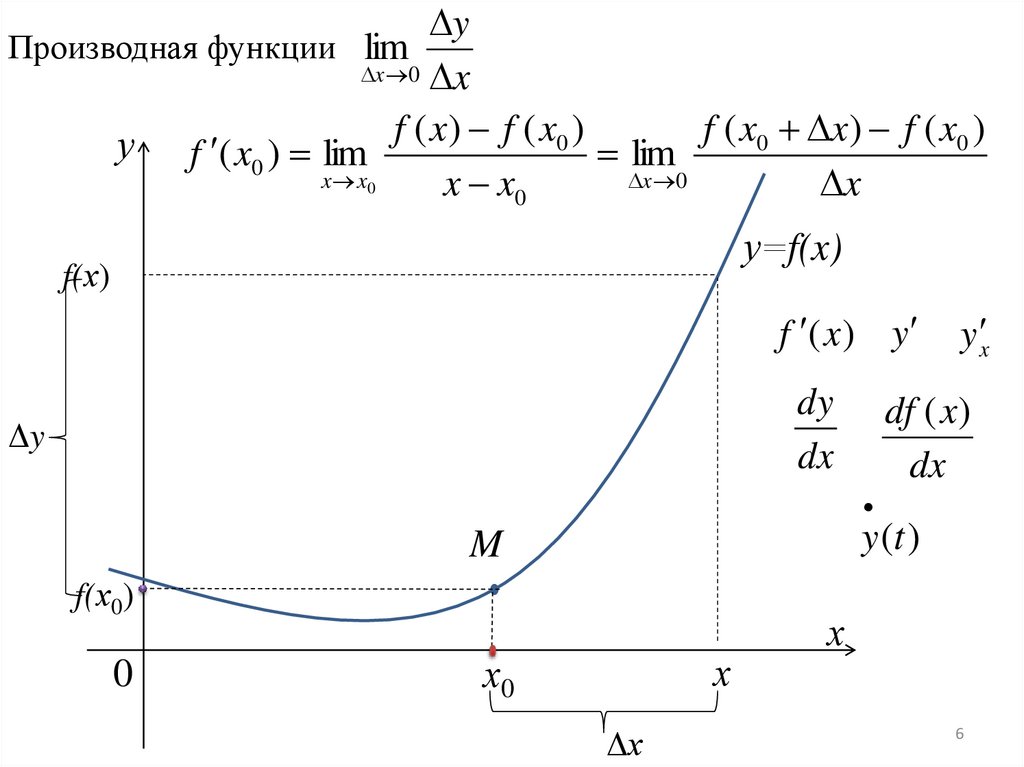
y
Производная функции lim
x 0 x
у f ( x0 ) lim f ( x) f ( x0 ) lim f ( x0 x) f ( x0 )
x x0
x 0
x x0
x
у=f(x)
f(х)
f (x ) y
dy
dx
Δy
y x
df ( x )
dx
y (t )
M
f(х0)
0
х
х0
Δх
х
6

7. Односторонние производные

• Функция y=f(x) непрерывна справа в точке х0.
• Правая производная (Δх>0)
f ( x) f ( x0 )
f ( x0 x) f ( x0 )
lim
x x0 0
x 0
x x0
x
f ( x0 ) lim
• Функция y=f(x) непрерывна слева в точке х0.
• Левая производная (Δх<0)
f ( x) f ( x0 )
f ( x0 x) f ( x0 )
lim
x x0 0
x 0
x x0
x
f ( x0 ) lim
f ( x0 ) f ( x0 ) f ( x0 ) f ( x0 )
f ( x0 ) f ( x0 ) не сущ. f ( x0 )
7

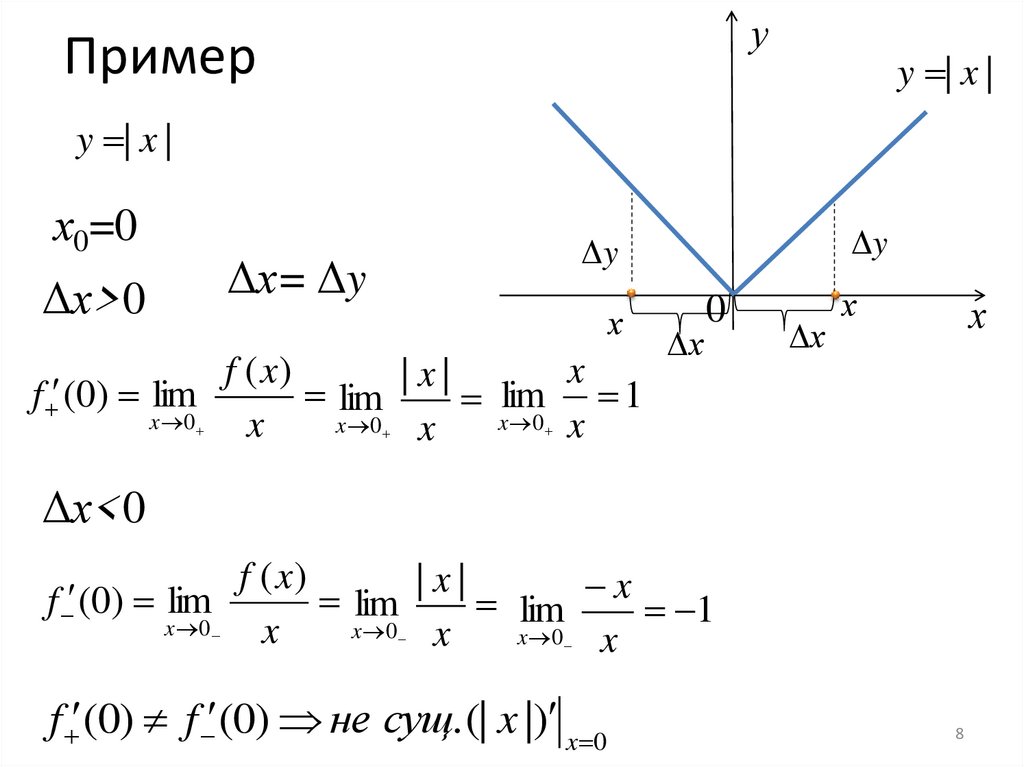
8. Пример

у
Пример
y | x |
y | x |
х0=0
Δх>0
Δх= Δy
Δy
Δy
х
f ( x)
x
|
x
|
f (0) lim
lim
lim 1
x 0
x 0 x
x 0 x
x
Δх
0
Δх
х
х
Δх<0
f ( x)
|
x
|
x
f (0) lim
lim
lim
1
x 0
x 0 x
x
x 0 x
f (0) f (0) не сущ. (| x |) x 0
8

9.

• Ньютон – флюксия; Лейбниц – дифференциал.
• differentia – разность
• Л. Эйлер (1707 – 1783) обозначение ∆
• Ж. Лагранж (1736 – 1813) обозначение у/
• Термин «производная (derivee)» в 1800г. в
книге фр. математика Л. Арбогаста.
• Процесс вычисления производной
называется дифференци́рованием.
• Функцию, имеющую конечную производную в
каждой точке интервала, называют
дифференцируемой в данном интервале.
9