Однородные дифференциальные уравнения 1 порядка

1.

4 Однородные дифференциальные
уравнения 1 порядка
Определение 1.
Функцию f(x;y)называют
однородной степени , если
справедливо тождество
f (tx; ty) t f ( x; y)

2.

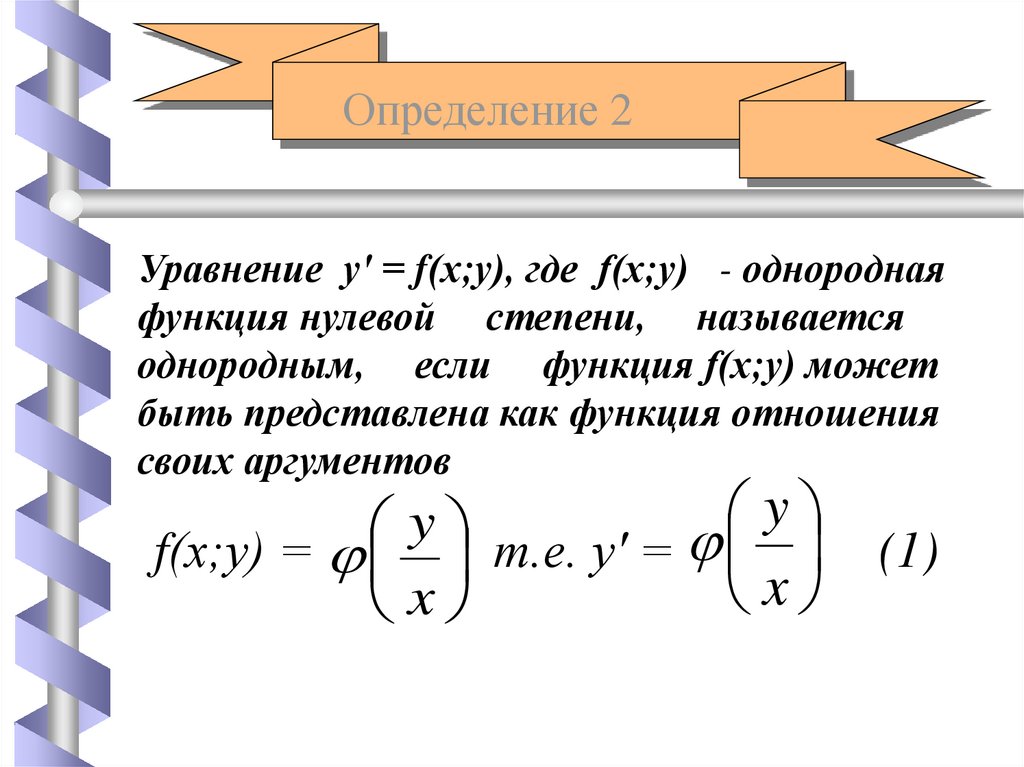
Определение 2
Уравнение у' = f(х;у), где f(х;у) - однородная
функция нулевой степени, называется
однородным, если функция f(х;у) может
быть представлена как функция отношения
своих аргументов
y
y
f(х;у) = т.е. у' =
x
x
(1)

3.

Уравнение у' = f(х;у)
Алгоритм решения:
1. Введем вспомогательную неизвестную
функцию y
u или у = хи
(2)
x
2. Тогда у' = (хи)' = и + хи‘ (3)
3. Подставляя (2) и (3) в (1) получаем
и + хи' = (и) - уравнение с
разделяющимися переменными

4.

du
x
(u ) u
dx
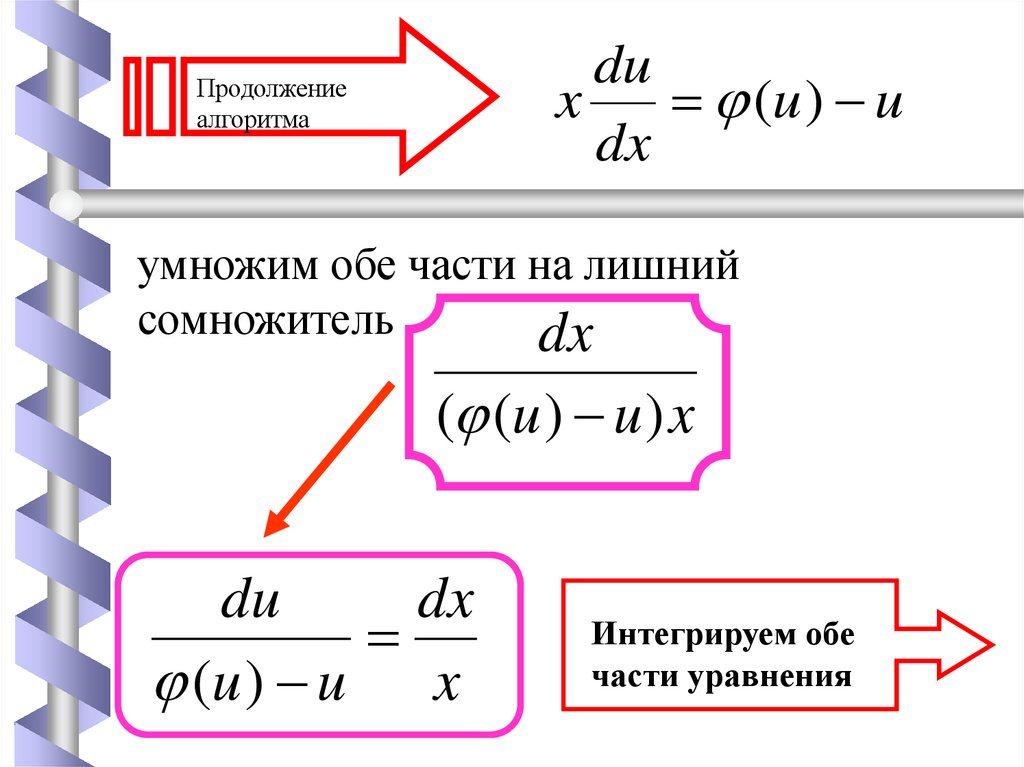
Продолжение
алгоритма
умножим обе части на лишний
сомножитель
dx
( (u ) u ) x
du
dx
(u ) u x
Интегрируем обе
части уравнения

5.

du
(u ) u ln x C
- общий интеграл дифференциального уравнения
4. Возвращаемся к переменным
у и х, получаем общее
решение однородного уравнения.
Предполагаем, что φ(и)-и 0

6.

Пример
Решить ДУ
(х-у)dх + хdу = 0
Разделить переменные нельзя как в
уравнении с разделяющимися переменными,
но можно все слагаемые разделить на х
y
1 dx dy 0
x
получили
однородное
уравнение.

7.

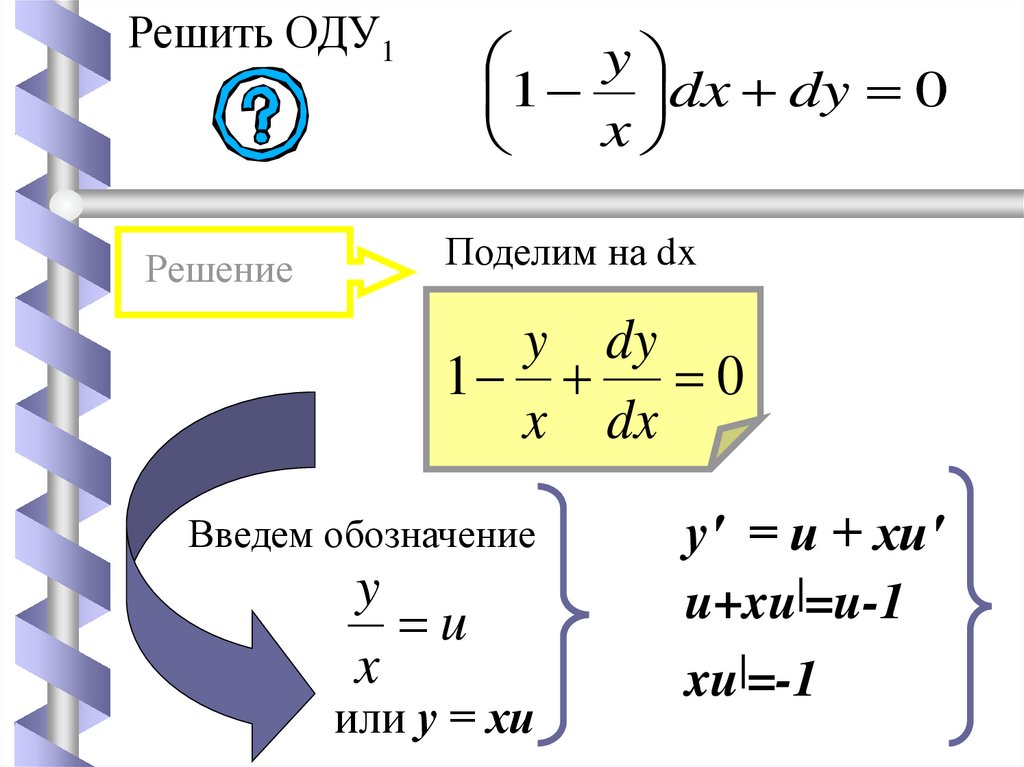
Решить ОДУ1
Решение
y
1 dx dy 0
x
Поделим на dx
y dy
1 0
x dx
Введем обозначение
y
u
x
или у = хи
у' = и + хи'
u+xu|=u-1
xu|=-1

8.

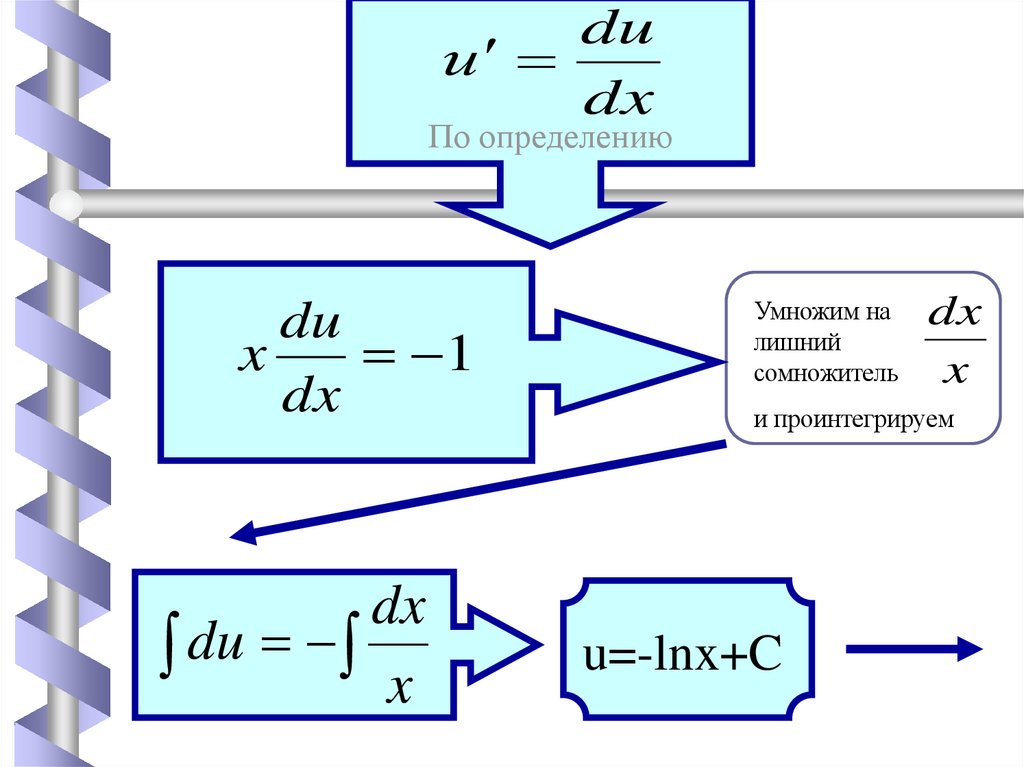
du
и
dx
По определению
du
x
1
dx
dx
du x
Умножим на
лишний
сомножитель
dx
x
и проинтегрируем
u=-lnx+C

9.

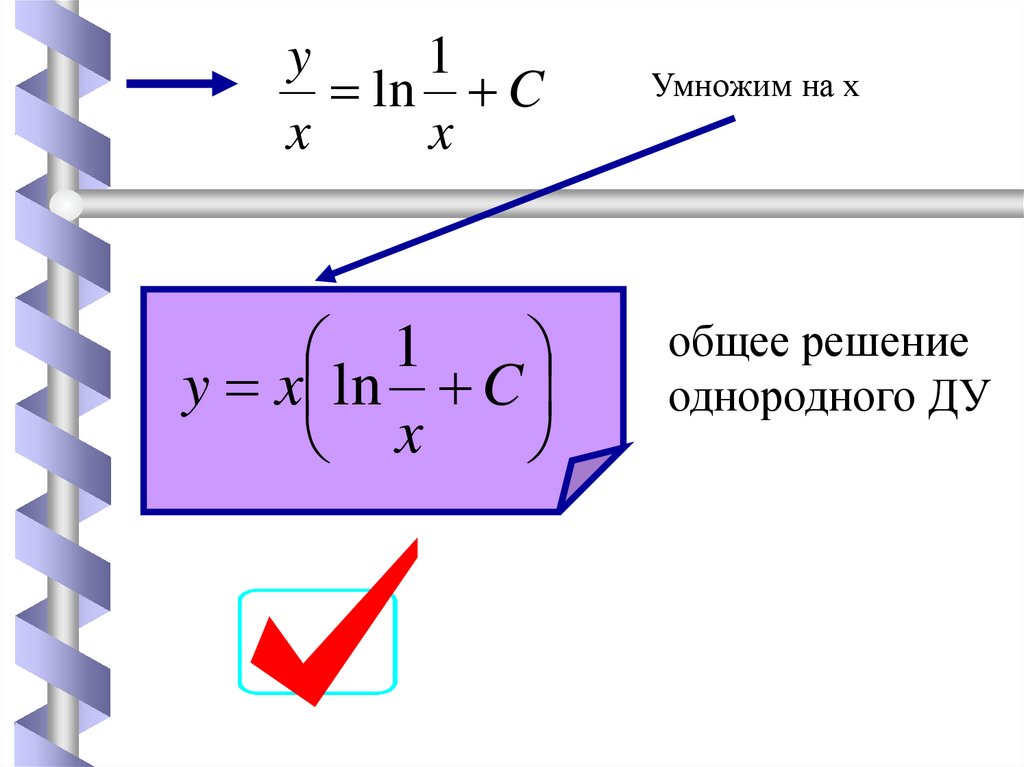
y
1
ln C
x
x
1
y x ln C
x
Умножим на х
общее решение
однородного ДУ