ДУ_4

1.

Лекция 6.
План лекции:
ЛДУn .
1.§11. ЛИНЕЙНЫЕ ДУn
ОСНОВНЫЕ ПОНЯТИЯ.
2. §12. ЛОДУ 2 С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ ( ЛОДУ 2 с ПК ).
1

2.

ЛДУn .
§11. ЛИНЕЙНЫЕ ДУn
ОСНОВНЫЕ ПОНЯТИЯ.
Df.1: Равенство, содержащее искомую функцию
у, её производные y , y ,....., ( y n )
в первой
степени, называется ЛДУn .
2
x
Пр.1: 2x 2 y y 3y
3
Общий вид ЛДУ n :
a 0 ( x )y
(n )
a 1 ( x )y
( n 1 )
ЛДУ 2 .
......... a n ( x)y f ( x)
(11.1),
2

3.

где коэффициенты a0 (x), a1 (x),....., an (x) и f(x) –
функции от х или постоянные, причём a 0 0.
Будем полагать, что a 0 1 , а функции
a1 (x), a2 (x),...., an (x), f (x) – непрерывные.
1) Если f(x) ≡ 0, то уравнение (11.1) называется линейным однородным (уравнение без
правой части); т.е.
y
(n)
a1 ( x)y
( n 1 )
...... an ( x)y 0
(11.2), 3

4.

2) Если f(x) ≡ 0, то уравнение (11.1) называется
линейным неоднородным (уравнение с правой
частью), т.е.
y ( n ) a1 ( x)y ( n 1) ....... an ( x)y f ( x)
(11.3).
4

5.

Df.2:
Функции y1 (x) и y 2 (x) называются линейно
зависимыми, если их отношение равно некоторой const λ: y 1 ( x)
(11.4),
y 2 ( x)
Если же
y 1 ( x)
const
y 2 ( x)
(11.5),
то y1 (x) и y 2 (x) – линейно независимые.
5

6.

Пр.2:
y 1 e x , y 2 e x , y 3 3e x .
y1 ex
1) x e 2 x const y 1 ( x), y 2 ( x)
y2 e
- линейно независимые,
y1
ex
1
2) x y 1 ( x), y 3 ( x)
y 3 3e
3
- линейно зависимые.
В дальнейшем будем рассматривать
ЛДУ 2 :
y a1 y a2 y f ( x)
6

7.

§12. ЛОДУ 2 С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ ( ЛОДУ 2 с ПК ).
Рассмотрим ЛОДУ 2 :
y a1 y a2 y f ( x)
(12.1)
Теорема:
(о структуре ОР ЛОДУ 2 ):
Если y1 (x) и y 2 (x) являются частными решениями ЛОДУ 2 : y a1 (x)y a2 (x)y 0, то функция
y c1y1 (x) c2y 2 (x) является ОР данного уравнения.
7

8.

Рассмотрим ЛОДУ 2 с ПК.
Df.1:
Равенство вида y py qy 0 (12.1),
где p и q – числа, называется ЛОДУ 2 с ПК.
Предположим, что y e , где k – число ,
является решением ЛОДУ 2 , т.е. удовлетворяет
уравнению (12.1).
kx
Тогда y (ekx ) kekx ,
kx
2 kx
y (ke ) k e
подставим в (12.1)
8

9.

k e pke qe 0
kx
2
e (k pk q) 0,
но e kx 0 ни при каких k (по свойству
показательной функции).
Получаем
=>
2 kx
kx
kx
k 2 pk q 0 (12.2).
(12.2) называется характеристическим уравнением ЛОДУ 2 (12.1).
Вывод: Если существует характеристическое
kx
уравнение (12.2) , то функция y e является
решением ЛОДУ 2 с ПК.
9

10.

Пр.1:
y 7 y 3y 0.
k 7k 3 0 - характеристическое уравнение.
2
Виды решений характеристического
уравнения.
1)
Если характеристическое уравнение (12.2)
имеет 2 различных корня k 1 k 2 ( т.е.
D > 0), то ОР ЛОДУ 2 имеет вид
y c1e
k 1x
c 2e
k 2x
, где y 1 ek x , y 2 ek x - ЧР
1
2
ЛОДУ 2 .
10

11.

2) Если характеристическое уравнение имеет 2
равных корня k 1 k 2 (D = 0), то ОР ЛОДУ 2
принимает вид:
k 1x
k 1x
k 1x
или
y
e
(c1 xc2 )
y c1e c 2 xe
0.0.
3) Если характеристическое уравнение имеет 2
комплексных корня k 1, 2 i, где , R
(D < 0), то ОР имеет вид:
y 0.0. e x (c1 cos x c 2 sin x ) , где
y 1 e x cos x,
x
y 2 e sin x.
ЧР ЛОДУ 2
11

12.

Пр.2:
y 5y 6y 0,
y x 0 1,
y x 0 0.
Решение:
1. Запишем характеристическое уравнение и
решим его: k 2 5k 6 0
k1 1; k 2 6.
2. Получаем:y e x , y e 6 x y 0.0. c1e x c 2e 6 x .
1
2
3. Найдём ЧР по заданным начальным условиям:
y 0.0. c1e x c 2e 6 x ,
y c1e 6c 2e
x
6x
.
=>
12

13.

1 c1e c 2e
0
6 0
,
0 c1e 0 6c 2e 6 0 ;
c1 c 2 1,
c1 6c 2 0.
решим систему методом Крамера:
а) вычислим основной определитель:
1 1
6 1 1 1 6 1 7 ,
1 6
б) вычислим определитель 1 для c1 :
1 1
1
6 1 0 1 6 0 6,
0 6
13

14.

в) вычислим определитель 2 для c2 :
1 1
2
1 0 1 1 0 1 1.
1 0
г) найдём c1 и c2 :
Отсюда
Пр.3:
1 6 6
c1
;
7 7
6 x 1 6x
y ч.0 e e
7
7
2 1 1
c2
.
7 7
- ЧР.
y 6y 9y 0.
Решение:
14

15.

k 2 6k 9 0
(k 3 ) 2 0
k 3 0
k 1, 2 3
Тогда:
y 1 e , y 2 xe
3x
3x
- ЧР.
y 0.0 c1e 3 x c 2 xe3 x - ОР.
Пр.4:
y 8y 25y 0.
Решение:
k 2 8k 25 0
15

16.

D 64 4 25 64 100 36 0, D 36i 2
8 36i 2
k 1, 2
;
2
8 6i
k1
4 3i;
2
т.е.
8 6i
k2
4 3i,
2
4, 3.
Тогда имеем:
y 0.0 e
4 x
(c1 cos 3x c 2 sin 3x ).
Zm.1: Решение ЛОДУ 2 с ПК не требует
операции интегрирования.
16

17.

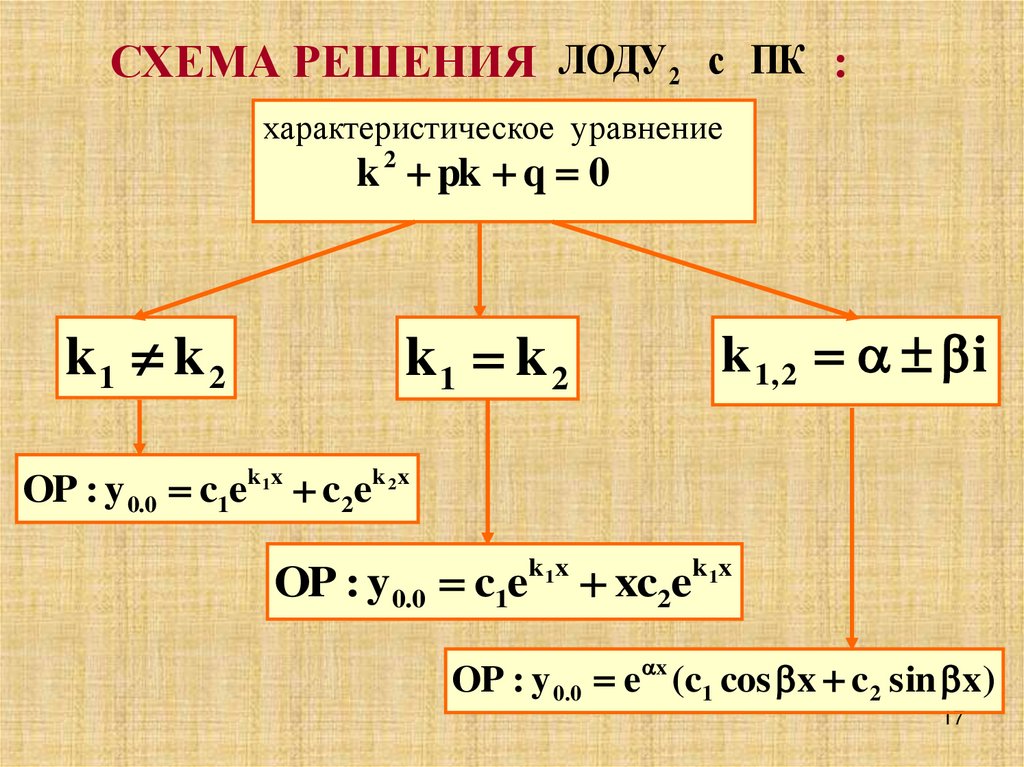
СХЕМА РЕШЕНИЯ ЛОДУ 2 с ПК :
характеристическое уравнение
k 2 pk q 0
k1 k 2
k1 k 2
k 1, 2 i
OP : y 0.0 c1ek1x c2ek 2x
OP : y 0.0 c1ek1x xc2ek1x
OP : y 0.0 e x (c1 cos x c 2 sin x)
17