Похожие презентации:
Tema_1
1.
Андреева Анна Дмитриевнаanya.2000@bk.ru
+7-920-292-51-92
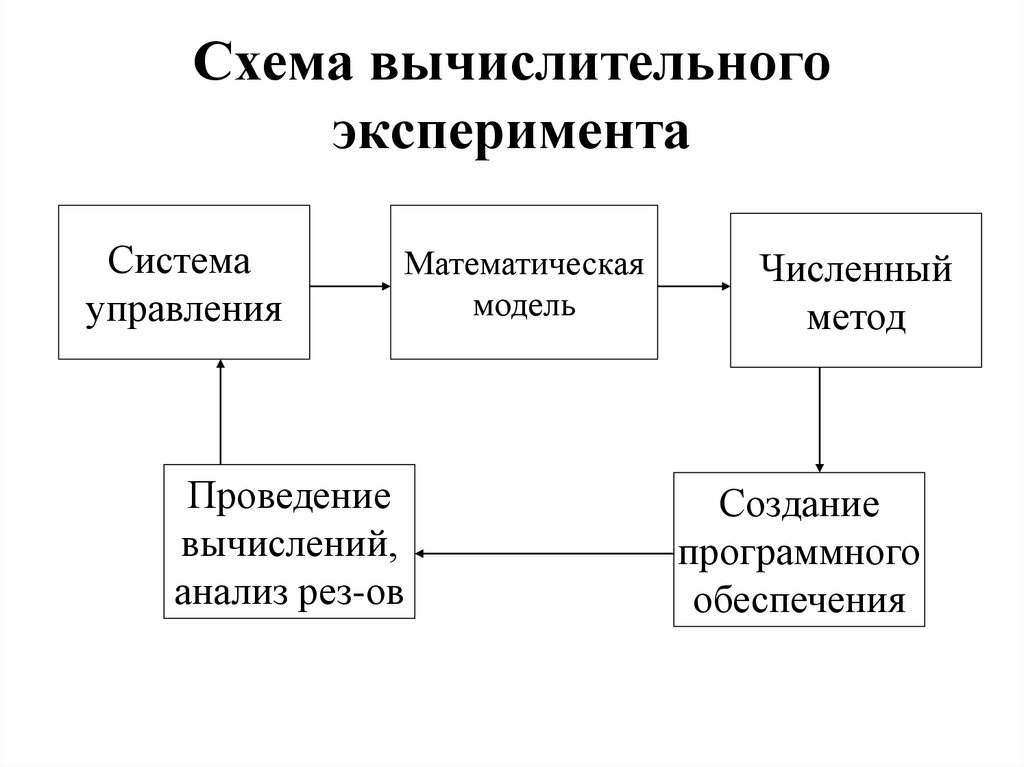
2. Схема вычислительного эксперимента
Системауправления
Математическая
модель
Проведение
вычислений,
анализ рез-ов
Численный
метод
Создание
программного
обеспечения
3.
Погрешность вычисленийx – точное значение числа
a – приближенное значение числа
Абсолютная погрешность:
x | x a |
Относительная погрешность:
x
x
x
Предельная погрешность Δa: |Δx| ≤ Δa
x [a a , a a]
4.
Множество X – совокупность определенных вполнеразличаемых объектов, рассматриваемых как единое
целое
Если между элементами множества установлены
соотношения или над ними определены операции, то
множество имеет структуру
Множество, наделенное структурой, называется
пространством
5. Метрическое пространство
Метрическое пространство – этомножество X с определенной на нем
метрикой d
Свойства расстояния (метрики) d:
x, y, z X
1. d ( x, y ) 0, причем d ( x, y ) 0, если x y
2. d x, y d y, x
3. d x, y d ( x, z ) d z , y
6. Примеры метрических пространств
1. x, y R множество вещественных чиселd1 x y
2. x, y R n множество векторов размерности n
1
p
p
d p xi yi
i 1
3. x t , y t C a ,b множество непрерывных
n
функций , определенных на отрезке a, b
d x, y max x t y t
t a ,b
7. Линейное пространство
- это множество X, между элементамикоторого определены линейные операции
Свойство
аддитивности:
x, y X , то x y z X , причем
x y y x
x ( y u) ( x y) u
x 0 x
x ( x) 0
x X , и R x z X , причем
Свойство
x x x
однородности:
x y x y
8. Вектор
- это упорядоченнаяпоследовательность
из n чисел
x1
x
xn
xТ x1 , , xn
Свойства векторов:
1. x y, если
xi yi , i 1, n
2. z x y сумма векторов размерности n
zi xi yi , i 1, n
3. z x y разность векторов, если
y z x
4. x x умножение вектора на скаляр
x x1 , , xn
9. Нормированное пространство
- это множество X, в котором существуетвозможность измерения значений элементов
Норма элемента (длина, модуль) x X :
1.
x 0, причем
2.
x x
3.
x y x y
x 0, если x 0
10. Примеры нормированных пространств
1. x R множество вещественных чиселx x
2. x R n множество векторов размерности n
1
p
p
x xi
i 1
3. x R n множество векторов размерности n
n
x max x1 , x2 , , xn
4. x t C a ,b множество непрерывных
функций , определенных на отрезке a, b
x t max x t
t a ,b
11.
x y d ( x, y)x, y, z X
1. d ( x, y ) 0, причем d ( x, y ) 0, если x y
2. d x, y d y, x
3. d x, y d ( x, z ) d z , y
1.
x 0, причем
2.
x x
3.
x y x y
x 0, если x 0
12. Скалярное произведение векторов
- это число, поставленное в соответствиепаре векторов x, y X :
x1
x ,
xn
y1
y
yn
n
x y xi yi
Т
i 1
Свойства скалярного произведения
1. xТ y y Т x
2. xТ y z xТ y xТ z
3. xТ y xT y
4. xT x 0, причем xT x 0, если x 0
13. Матрицы. Определения
Матрица A – таблицавещественных (или
комплексных) чисел,
содержащая m строк
и n столбцов
a11 a12 a1n
a a a
21 22
2n
A
aij
am1 am 2 amn
При m 1 : A a1 an
- вектор строка
a1
При n 1 : A
a m
- вектор столбец
m×n
При m = n – квадратная матрица
14. Матрицы. Определения
a11 0 00 a 0
22
A
0 0 ann
1 0 0
0 1 0
E
0 0 1
- диагональная матрица
- единичная матрица
t11 0 0
t t 0
Tn 21 22
t n1 t n 2 t nn
t11 t12 t1n
0 t t
2n
T n 22
0 0 t nn
- нижняя треугольная матрица
- верхняя треугольная матрица
15. Операции над матрицами
Am n aij , Bm n bij1. A B, если a b , i 1, m; j 1, n
2. C A B, C c
ij
ij
m n
ij
cij aij bij , где i 1, m; j 1, n
3. C A B, C
m n
cij
cij aij bij , где i 1, m; j 1, n
4. C A, C
m n
cij
cij aij , где i 1, m; j 1, n
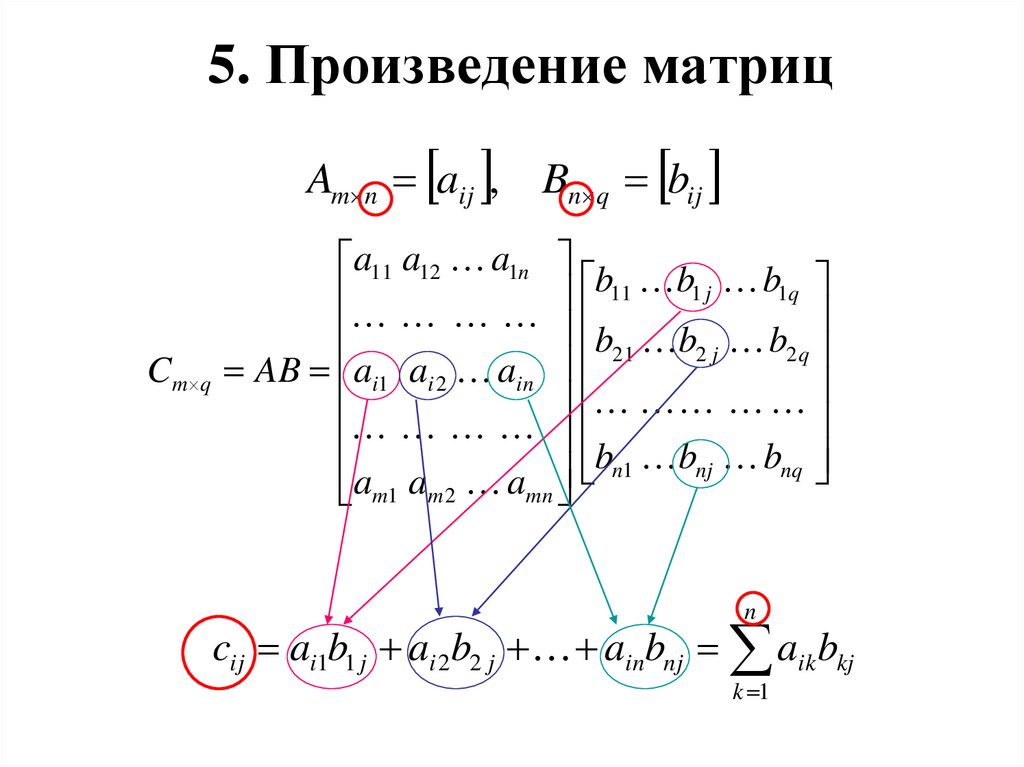
16. 5. Произведение матриц
Am n aij , Bn q bija11 a12 a1n
b11 b1 j b1q
b21 b2 j b2 q
Cm q AB ai1 ai 2 ain
b b b
nj
nq
am1 am 2 amn n1
n
cij ai1b1 j ai 2b2 j ainbnj aik bkj
k 1
17. Транспонирование матриц
Am n aija11 a12 a1n
a a a
2n
A 21 22
am1 am 2 amn
( A B)T AT BT
AT n m aT ij , где
aT ij a ji , i 1,n; j 1,m
a11 a21 am1
a a a
m2
AT 12 22
a
a
a
1n 2 n
mn
( AB)T AT BT
18.
Определитель квадратной матрицыa11 a12 a1n
det A
a21 a22 a2 n
an1 an 2 ann
a11 a1, j 1 a1, j 1 a1n
ai 1 ,1 ai 1 , j 1 ai 1, j 1 ai 1,n
M ij
ai 1,1 ai 1, j 1 ai 1, j 1 ai 1,n
an1 an , j 1 an , j 1 ann
Aij ( 1)i j M ij
n
det A aij * Aij
i 1
n
det A aij * Aij
j 1
19.
Норма матрицы1. A 0, причем A 0, тогда и только тогда, когда A 0
2. A A , - некоторое число
3. A B A B
4. AB A B
n
A 1 max aij
1 i m
j 1
m
A 2 max aij
1 j n
A3
m
i 1
n
a
i 1 j 1
ij
2
20.
Обратная матрица1
1
AA A A E
1
T
Aij
A
det A
1
21.
Ранг матрицы-указывает на число линейнонезависимых строк (столбцов) матрицы
r = rang A
Минор k-го порядка, M k – определитель,
составленный из произвольно выбранных
k строк и k столбцов матрицы
Теорема.
Если в матрице A существует минор r-го
порядка не равный нулю, а все окаймляющие
его миноры (r+1)-го порядка равны нулю, то
r – ранг матрицы
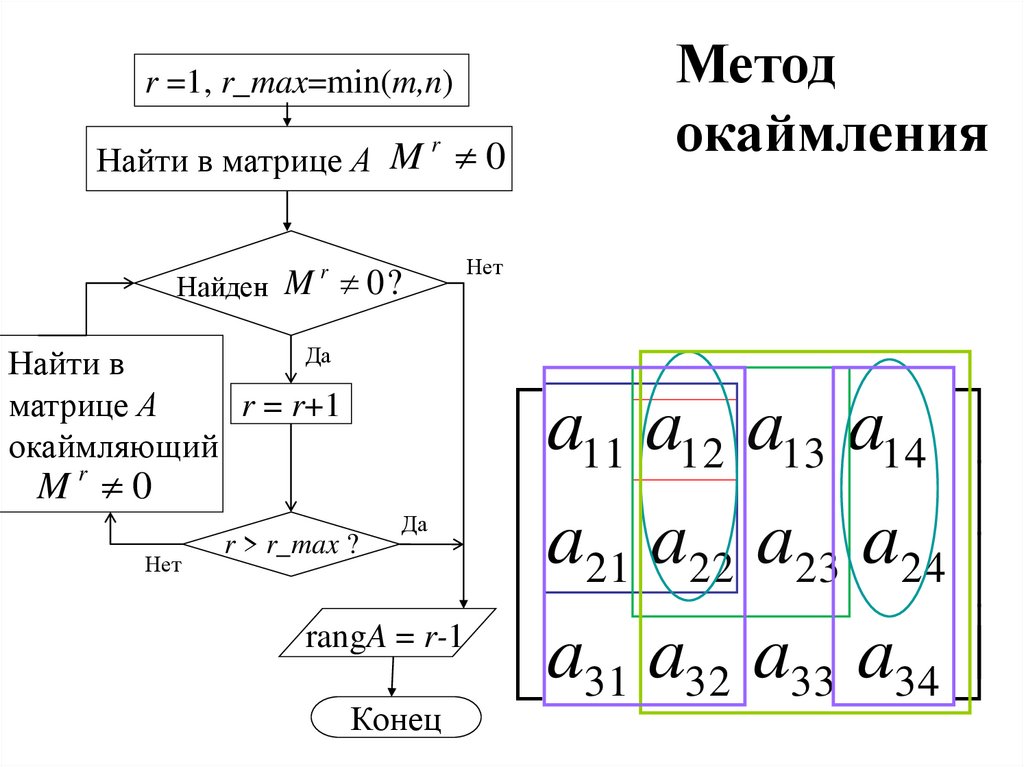
22.
Окаймляющим для минора r-го порядкабудет минор порядка r+1, полученный из
исходного добавлением одной строки и
одного столбца матрицы
M
2
1
M 22
M 32
M1
a11 a12 a13 a14
a a a a
21 22 23 24
a31 a32 a33 a34
M 42
23.
Замечания:1.rang A=0, тогда и только тогда, когда А=0
2. rang An n n, когда det А≠0
3. rang Am n min m, n
24.
r =1, r_max=min(m,n)r
M
0
Найти в матрице А
r
Найден M 0 ?
Да
Найти в
матрице А
r = r+1
окаймляющий
Mr 0
Нет
Метод
окаймления
Нет
a11 a12 a13 a14
a a a a
21 22 23 24
rangA = r-1
a31 a32 a33 a34
Конец
r > r_max ?
Да
25. Системы линейных алгебраических уравнений
a11x1 a12 x2 a1n xn f11
a x a x a x f
21 1 22 2
2n n
2
am1 x1 am 2 x2 amn xn f m
Аx f
2
m – количество уравнений системы
n – количество неизвестных системы
матрица коэффициентов
a11 a12
a
a22
21
A
am1 am 2
a1n
a2 n
amn
x1
x
x 2
xn
f1
f
f 2
fm
вектор неизвестных
заданный вектор
26.
Совместность системлинейных уравнений
Система называется совместной, если она имеет хотя бы одно
решение.
Теорема Кронекера-Капелли
Система линейных алгебраических уравнений совместна тогда и
только тогда, когда ранг матрицы коэффициентов системы равен
рангу расширенной матрицы системы, т.е. rang A=rang A|f.
a11 a12
a
a22
21
A
am1 am 2
a1n
a2 n
amn
a11
a
A f 21
am1
a12
a22
am 2
a1n f1
a2 n f 2
amn f m
27.
Количество решений системылинейных уравнений
Следствие из теоремы Кронекера-Капелли
Если rang A ≠ rang A|f ,
то СЛАУ несовместна (не имеет решений)
Если rang A = rang A|f <n,
то СЛАУ является неопределённой (имеет бесконечное к-во
решений)
Если rang A = rang A|f =n,
то СЛАУ является определённой (имеет единственное решение)
28. Прямые методы. Метод Гаусса
m=n, det A≠0 → rang A = mПрямой ход – приведение матрицы А к верхнему треугольному виду
Обратный ход – нахождение неизвестных системы
a 21a m 1
a11a11
Первый шаг:
a11 x1 a12 x2 a1m xm f1
a x a x a x f
2m m
2
+ 21 1 22 2
a m1 x1 a m 2 x2 a mm xm f m
+
a11 х1 a12 х2 a1m хm f1
(1)
(1)
(1)
a
x
a
x
f
22 2
2m m
2
a (1) x a (1) x f (1)
m2 2
mm m
m
(1)
ij
a
ai1
aij
a1 j ,
a11
f i (1) f i
ai1
f1
a11
3
29.
Метод Гаусса4
k-ый шаг:
f1
a11x1 a12 x2 a1k xk a1m xm
(1)
a22
x2 a2(1k) xk a2(1m) xm f 2(1)
ak( k 1,2k) 1 xk 1 ak( k 1,2k) xk ak( k 1,2m) xm f k( k1 2)
( k 1)
( k 1)
( k 1)
a ( k 1)
a
x
a
x
f
ik
k
m
kk
km
k
( k 1)
akk
( k 1)
( k 1)
amk
xk amm
xm f m( k 1)
+
( k 1)
( k 1)
akk
xk ak( k, k 11) xk 1 akm
xm f k( k 1)
a k( k )1, k 1 xk 1 ak( k )1, m xm f k( k1)
(k )
(k )
(k )
a
x
a
x
f
k 2, k 1 k 1
k 2, m m
k 2
a m( k,)k 1 xk 1 am( k,)m xm f m( k )
aik( k 1) ( k 1)
(k )
( k 1)
aij aij
( k 1) akj ,
akk
fi
(k )
fi
( k 1)
aik( k 1)
( k 1)
f
,
( k 1) k
akk
i, j k 1, m ; k 1, m 1
5
30. Обратный ход метода Гаусса
a11х1 a12 х2a1m xm f1
(1)
a22
x2 a2(1m) xm f 2(1)
( m 2)
( m 2)
( m 2)
a
x
a
x
f
m 1, m 1 m 1
m 1, m m
m 1
( m 1)
( m 1)
a
x
f
mm
m
m
7
a1m
a11 a12
0 a (1)
a2(1m)
22
*
A 0 0
( m 2)
( m 2)
a
a
m 1, m 1 m 1, m
( m 1)
0 0
0
amm
xm
xm 1
6
f m( m 1)
( m 1)
amm
f m( m 1 2) am( m 1,2m) xm
am( m 1,2m) 1
m
1 ( k 1)
( k 1)
xk ( k 1) f k
ak , j x j , k 1, m
akk
j k 1
8
31. Метод Гаусса с выбором главного элемента
a1k xk a1m xmf1
a11x1 a12 x2
(1)
a22
x2 a2(1k) xk a2(1m) xm
f 2(1)
11 ( k 2)
ak 1,k 1 xk 1 ak( k 1,2k) xk ak( k 1,2m) xm f k( k1 2)
( k 1)
( k 1)
akk
xk akm
xm f k( k 1)
( k 1)
( k 1)
amk
xk amm
xm f m( k 1)
a11 a12 a1k a1m f1
(1)
(1)
(1)
(1)
0
a
a
a
22
2m f 2
2k
.......... .......... .......... .......
A( k 1)
(
k
1
)
(
k
1
)
(
k
1
)
0
0 akk akm f k
..........
..........
..........
.........
( k 1)
( k 1) ( k 1)
0
0
a
a
mm f m
mk
1. по столбцу
( k 1)
aik( k 1) akk
, k 1 i m
32. Метод Гаусса с выбором главного элемента
11a11 a12 a1k a1m f1
(1)
(1)
(1)
(1)
0
a
a
a
22
2m f 2
2k
.......... .......... .......... .......
( k 1)
A
(
k
1
)
(
k
1
)
(
k
1
)
0
0 akk akm f k
..........
..........
..........
.........
( k 1)
( k 1) ( k 1)
0
0
a
a
mm f m
mk
2. по строке
( k 1)
akj( k 1) akk
, k 1 j m
3. по всей матрице
aij( k 1) akk( k 1) , k 1 i m,
k 1 j m
33.
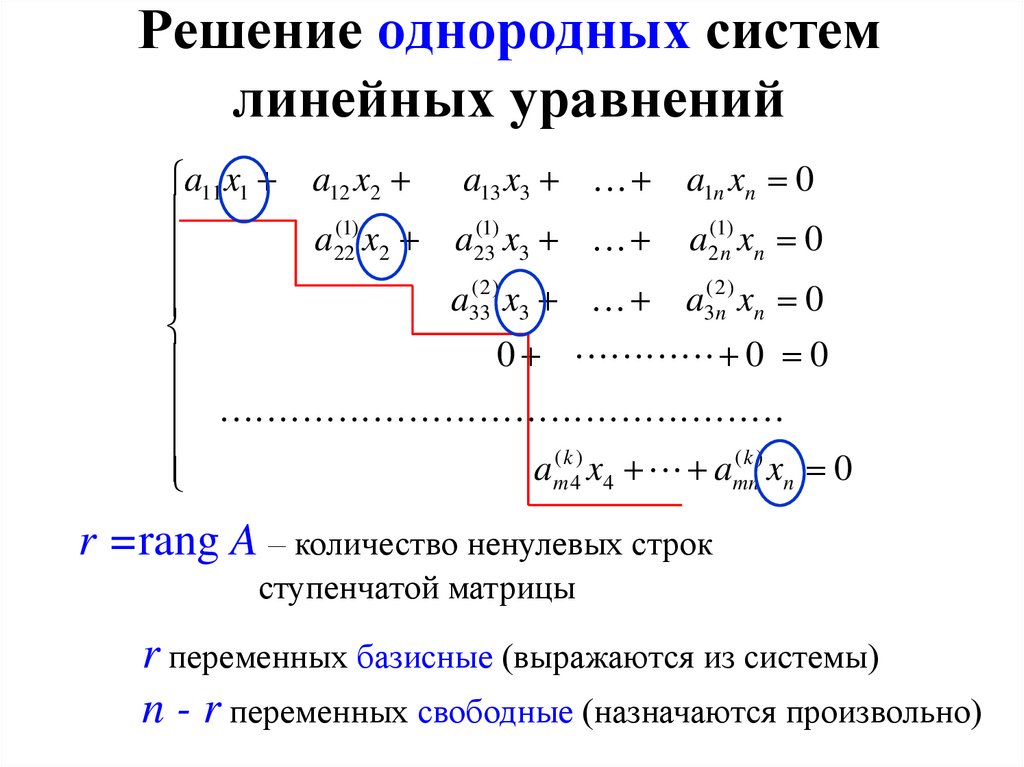
Решение однородных системлинейных уравнений
a11 x1 a12 x2 a1n xn 0
a x a x a x 0
21 1 22 2
2n n
am1 x1 am 2 x2 amn xn 0
• Если rang A ≠ rang A|f , то СЛАУ несовместна
• Если rang A = rang A|f <n, то СЛАУ является
неопределённой
• Если rang A = rang A|f =n, то СЛАУ является
определённой
x=0
34.
Решение однородных системлинейных уравнений
a11 x1 a12 x2 a13 x3 a1n xn 0
(1)
(1)
(1)
a
x
a
x
a
22 2
23 3
2 n xn 0
( 2)
a33
x3 a3( 2n) xn 0
0 0 0
(k )
am( k4) x4 amn
xn 0
r =rang A – количество ненулевых строк
ступенчатой матрицы
r переменных базисные (выражаются из системы)
n - r переменных свободные (назначаются произвольно)
35.
Решение однородных системлинейных уравнений
Общее
решение
однородной
СЛАУ
Любая совокупность (n − r) линейно независимых решений xi,
(i = 1, …, n-r) однородной СЛАУ называется
фундаментальной системой решений (ФСР)
Общее решение:
X= C1⋅x1 +C2⋅x2 +…+ Cn-r⋅xn-r
36. Вычисление определителя
a11a
A 21
a m1
a12
a 22
am2
a1m
a11 a12
0 a (1)
a2(1m)
22
*
A 0 0
( m 2)
( m 2)
a
a
m 1, m 1 m 1, m
( m 1)
0 0
0
amm
a1m
a 2 m
a mm
m
det A det A 1 aii
r
i 1
13
37.
Применение элементарныхнижних треугольных матриц
Шаг 1:
Ax = f
A(1)x = f(1)
aij(1) aij
ai1
a1 j ,
a11
f i (1) f i
ai1
f1
a11






































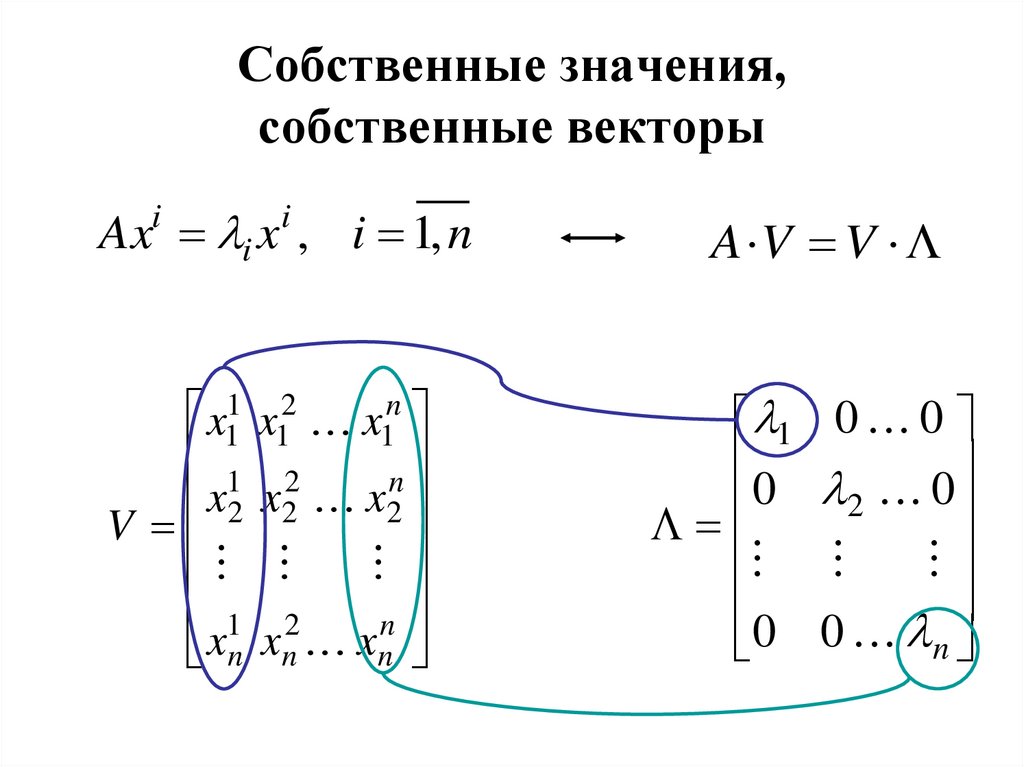



 Математика
Математика








