Автомодельность и бегущие волны

1.

Автомодельность и бегущие волны
Явление, развивающееся во времени, называется автомодельным, если
распределения его характеристик в разные момент времени
получаются одно из другого преобразованием подобия.
w x,t W z
z kx t

2.

Решения типа бегущей волны
z kx t
w x,t W z
w x,t W z 1
w x x,t kW z
t
Уравнения не зависят явно от независимых переменных.

3.

Решения типа бегущей волны

4.

бегущей
Решения
типа
волны
2
2
w
x,t
w
x,t
w
x,t
f
w
x,t
f
w
f
w
2
x
x
x
x
2
2
2
2
k f W W z k f W W z k f W W z
w x,t W z
z kx t
2
k и произвольные постоянные
k f W W dz W z dz
k f W W W C
3
dW
k f W
W C
dz
f W dW
k
dz
2
2
1
2
1
2
W C1
k
2
k
2
f W dW
W C1
f W dW
W C1
dz
z C2

5.

Решения типа бегущей волны
z kx t
w x,t W z
k и произвольные постоянные
a w x,t
w x,t
t
2
2
x
2
2
x
a 2 k 2W z W z 0
W z C1 C2e
t
z
a2k 2
a 2 k 2 2 0
a 2 k 2 0
1 0 , 2 2 2
a k
w x,t C1 C2e
w x,t k W z
w x,t W z
w x x,t kW z
kx t
a2k 2

6.

Решения типа бегущей волны
z kx t
w x,t W z
a w x,t w x,t
x
t
x
w x,t
2
a k W z W z W z 0
2
2
a 2 k 2 WdW
dz,
W
a 2 k 2W z W z W z C1
Если функция W обращается в
ноль хотя бы в одной точке z0, то
константа равна нулю.
a 2 k 2W z W z W z C1
a 2k 2
W z C2 ,
w x,t
W
2
ak
2
kx t C.
ak
2
2
z C,

7.

Решения типа бегущей волны
z x t
w x,t W z
k w x,t w x,t
x
t
x
w x,t
n
0
n
W z k0 W z W z 0
n
k0
W z W z W z C1
Если функция W обращается в ноль хотя бы в одной точке z0, то
константа равна нулю.

8.

Решения типа бегущей волны
k0
n
W z W z W z
k0
n 1
W z
dW z dz
k0
dW z dz
n 1
W z
Проинтегрируем от z0 до z
n
W z
z0 z
k0
n
k0
W z z0 z
n
Доопределим решение для z0<z
1
n
1
n
W z 0,z z0
n
w x,t
x0 x t ,x x0 t ; w x,t 0,x x0 t
k0
Чтобы решение существовало условия задачи должны быть согласованы,
1
например на полупрямой t>0, x>x0
2 nt n
w x,0 0,x x0
w x0 ,t
,t 0
k0

9.

Уравнение Монжа — Ампера
Уравнения Монжа — Ампера часто возникают в дифференциальной геометрии,
например в дифференциальной геометрии поверхностей.
Впервые они были изучены Гаспаром Монжем в 1784 году и позднее Андре-Мари
Ампером в 1820 году.

10.

2u
2
x
2u
t x
Решения типа бегущей волны
2u
2
2
2
2
x t u u u
w
W z
x,t
2
2
z kx t
2
u x t x t
2
t k и произвольные постоянные
2
kW z 2W z
0
k 2W z
В математике уравнение Монжа–Ампера представляет собой нелинейное уравнение в
частных производных второго поряда специального вида. Уравнение второго порядка для
неизвестной функции u двух переменных x,y относится к типу Монжа-Ампера, если оно
линейно по определителю матрицы Гессе от u и по частным производным второго порядка
от u.

11.

Решения типа бегущей волны
Инвариантность уравнений относительно сдвига
x x C1
t t C2
Но условие инвариантности этих преобразований не является
необходимым условием существования решения типа бегущей волны

12.

Уравнение Бюргерса
Уравнение названо в честь Иоганна Мартинуса Бюргерса (1895—1981). Является
частным случаем уравнений Навье — Стокса в одномерном случае.

13.

Решения типа бегущей волны
u x,t f
z Vt
Уравнение Бюргерса
u x,t f u x,t Vf
u x x,t f
xx
t
f f f Vf 0

14.

Уравнение Бюргерса
f z f z f z Vf z 0
1 2
f z f z Vf z 0
2
1 2
f z f z Vf z C
2
f z , f z 0,z
C 0

15.

Уравнение Бюргерса
1 2
f z f z Vf z 0
2
1
1
V 0
V
2
2
1 2
1
f z f z f z 0
2
2
2 f f f 1
df
df
dz
f 1 f 2
dz
f f 1 2
df
1 f
e 2
f
z
z
2
ln 1 f ln f
f
1
1 e
z
2

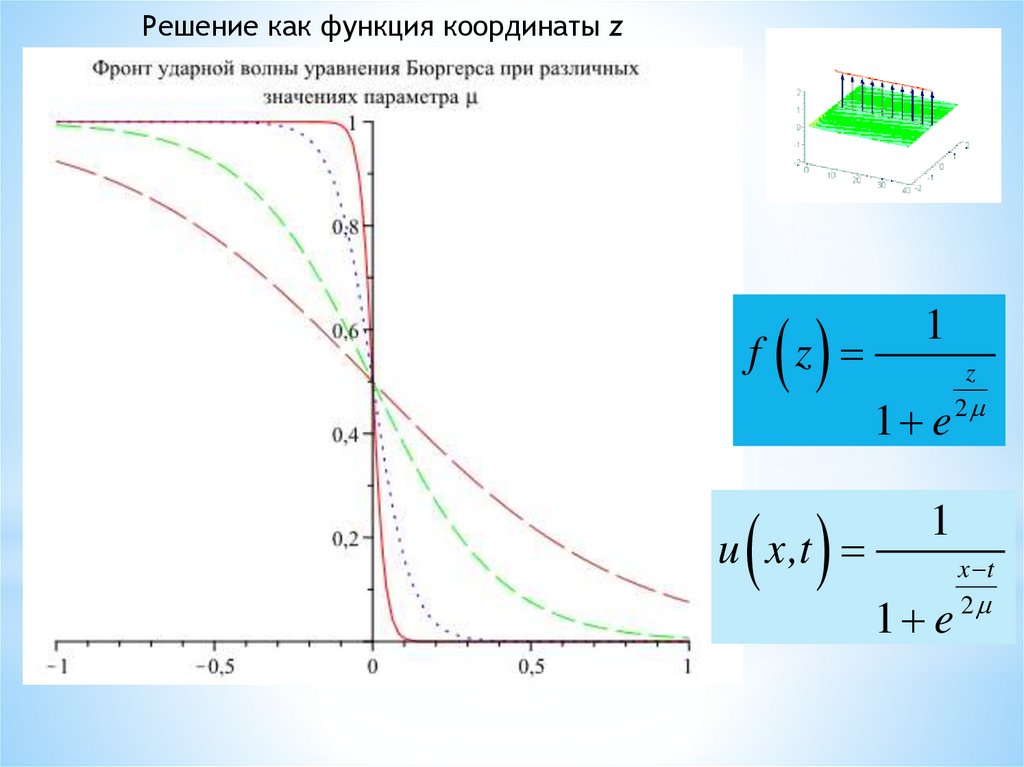
16.

Решение как функция координаты z
f z
u x,t
1
1 e
z
2
1
1 e
x t
2

17.

Уравнение Бюргерса

18.

19.

20.

21.

22.

Решения типа бегущей волны
z x Vt
u x,t f z
Уравнение Кортевега — де Фриза
u x,t Vf z
xxx
Vf x,t
z 0 f z
ux x,tf z f2 fz z u
f z 6 f z2 f z Vf z 0
f tz 3 f 2 z Vf z С1

23.

Уравнение Кортевега — де Фриза
f z 3 f
2
z Vf z С 0
1
f z f z 3 f 2 z f z Vf z f z С1 f z 0
2
1
2
V
f z f z f z С1 f z 0
2
2
2
2
1
V 2
3
f f f С1 f С2 0 f f 2 V 2 f
2
2
V V 2f
V V 2f
df
df
1
V
f V 2f
d
ln
e
d
f V 2f
V
V V 2f
V V 2f
V
V
V
V
2
0
V sh
V 2 f ch
V V 2 f e V V 2 f 0 2e
2
2
V
V 2 f V th
V
2
V 2 f Vth 2
V
2
2
V
V
2
e
2
e
2
ch 2
V
sh
V
V
V
2
2
4
f
2
2
V
V
V
2
2
2
ch
2ch
2c
h
2
2
2

24.

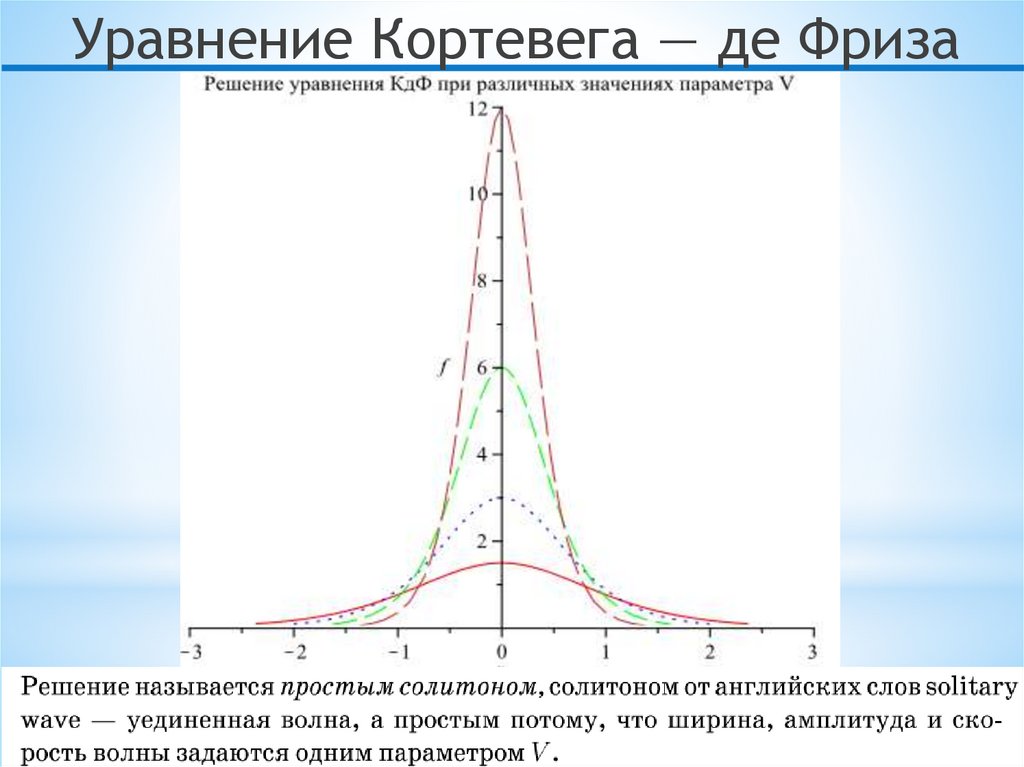
Уравнение Кортевега — де Фриза

25.

Уравнение Кортевега — де Фриза
u x,t g z
z x Vt

26.

27.

Автомодельные решения

28.

Автомодельные решения
Автомодельность – это симметрия задачи, позволяющая скомпенсировать
масштабные преобразования независимых переменных соответствующих
растяжениям решения.

29.

30.

t C 1t
x C k x
w C mw
Найдем связь между параметрами и в решении и параметрами k и m в
преобразовании растяжения-сжатия. Пусть решение уравнения
-m
k
C
w = C t U Cw xC
xt, t
Тогда решение преобразованного уравнения
w=
U xtxt
tt U
w C m t U C k xt
w x, t
Чтобы решения совпали при любых C≠0,
следует положить
m, k

31.

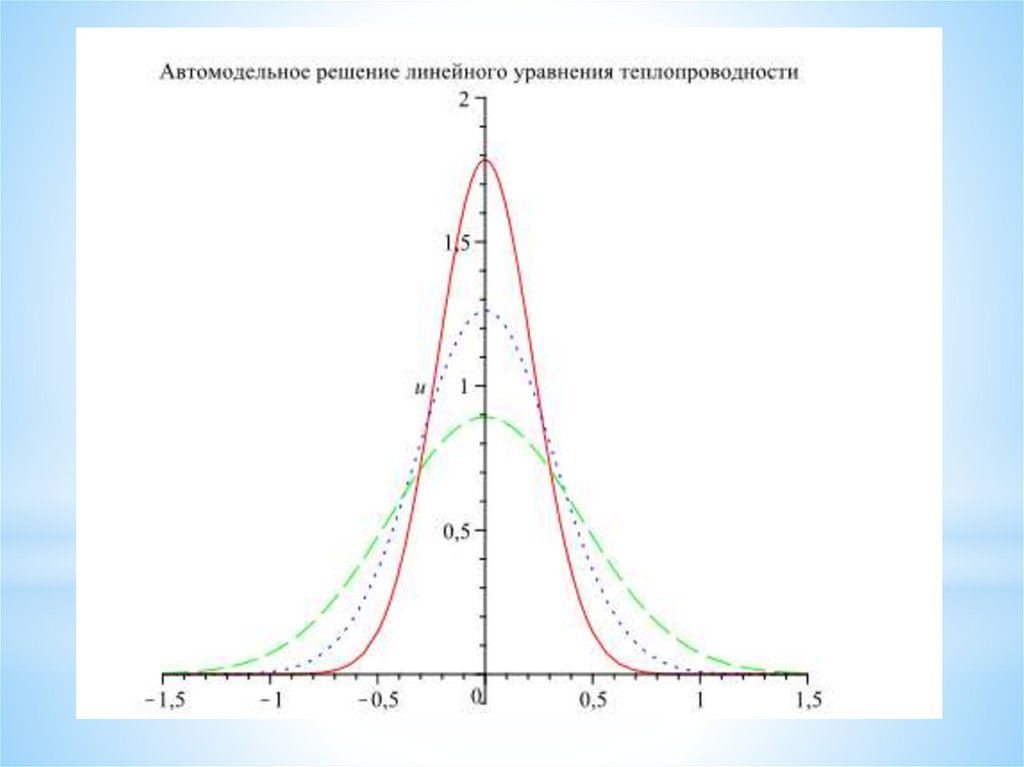
Функция Грина

32.

В случае уравнений, зависящих от одной пространственной переменной,
автомодельность означает выбор нового масштаба координаты l(t) и решения u (x,
t) так, что в новых координатах решение является функцией одной переменной ξ.
1
i x
x
e
d
2
k
k
k
C
1
C
i C x
i x
k
C k x
e
d
e
d
C
m x
k
w C w
2
d C d 2
2
t Ct , t C 1t
C
m 1
w
m 2k w
C
t
x 2
C w x , 0 C x
m
k
m 1 m 2k
x C k x , x C k x
1
C m w x , 0 C k x k
2
1
m k
2

33.

1
m k
2
1, k 1
m
,
2
2
ut
t
3
2
3
2
xt
f
f t
2
2
1
2
t
3
2
2
f
t
3
2
2
f , u xx t
1
2
f t
1
2
2

34.

1
1
f f f 0
2
2
1
f f 0
2

35.

36.

37.

w C mw
t Ct , t C 1t
x C k x , x C k x
C
m 1
w
w
2m 2k
C
w
t
x x
C mw x , 0 C k x
C m w x , 0 C k x
m k ; m 1 2m 2k
1
1
k ; m
3
3
1
1
,
3
3

38.

1
1
ff f f 0
3
3
1
ff f 0
3

39.

40.

w C mw
t Ct , t C 1t
x C k x , x C k x
m, k
1
m k
2