Похожие презентации:
Численное интегрирование
1. Численное интегрирование
ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ§1. Приближенные методы вычислений определенных интегралов
Формула Ньютона-Лейбница для вычисления определенного интеграла имеет
вид
.
b
f ( x) dx F (b) F (a)
a
Однако, вычисление по этой формуле не всегда возможно.
В таких случаях используются приближенные методы вычисления интегралов.
Наиболее употребительными среди них являются метод прямоугольников,
метод трапеций и метод парабол.
2.
cf ( x) dx
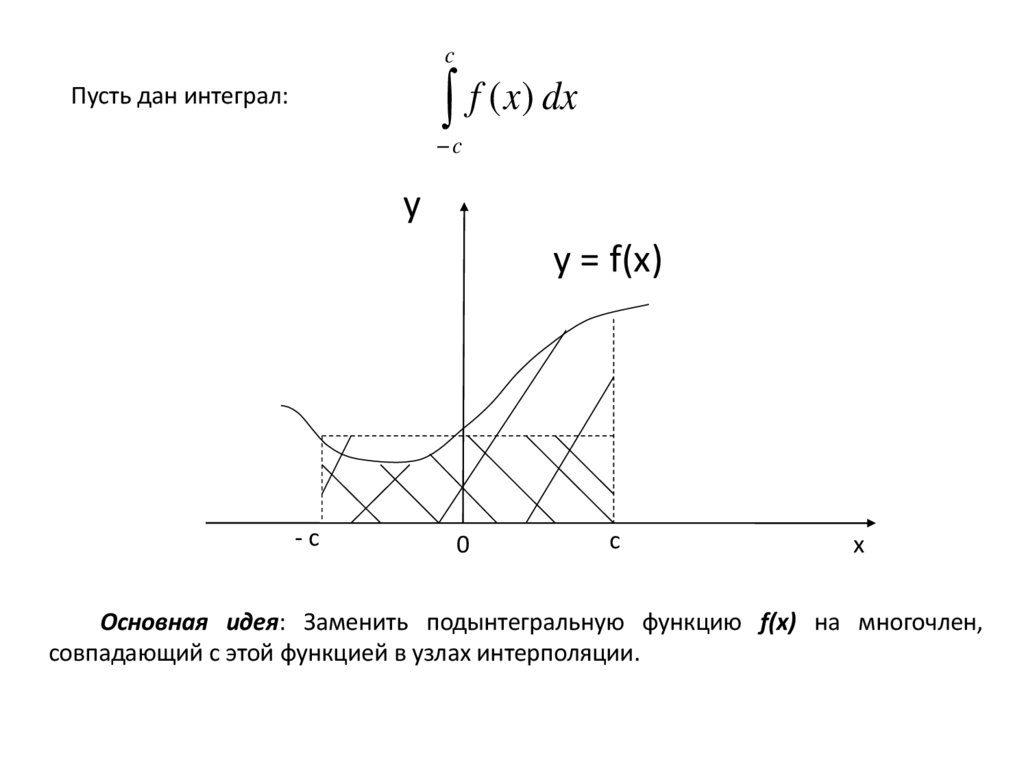
Пусть дан интеграл:
c
y
y = f(x)
-c
0
c
x
Основная идея: Заменить подынтегральную функцию f(x) на многочлен,
совпадающий с этой функцией в узлах интерполяции.
3.
1)f(x) заменим многочленом нулевого порядка y = f(0):
c
f ( x ) dx f(0) 2c
c
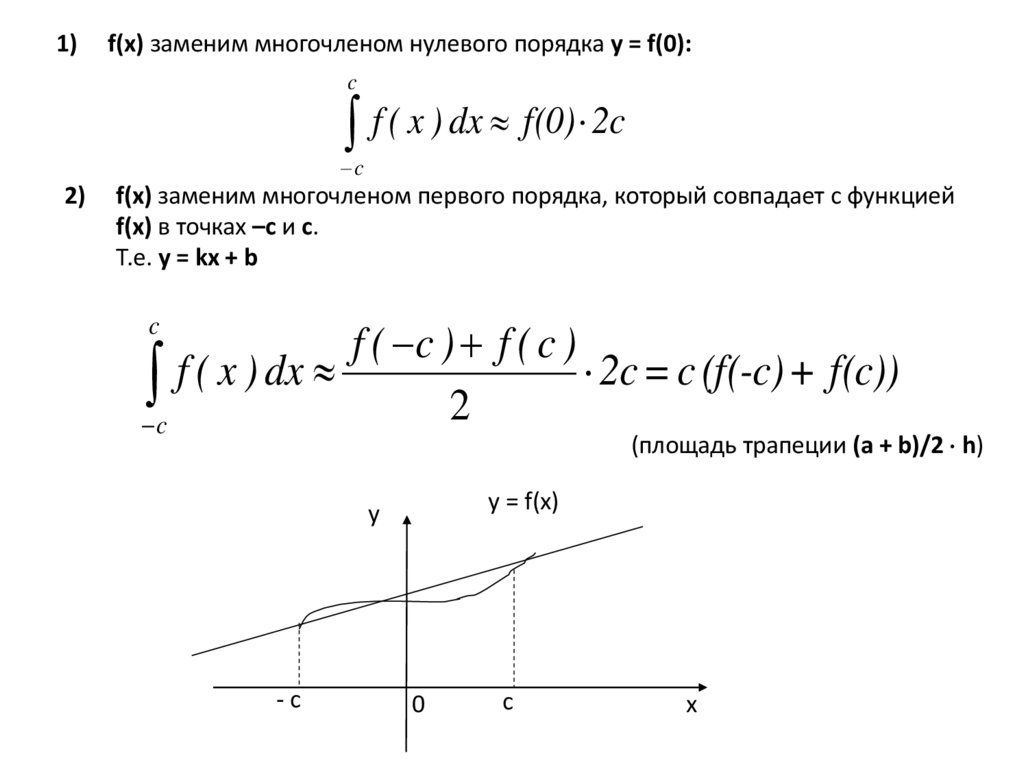
2)
f(x) заменим многочленом первого порядка, который совпадает с функцией
f(x) в точках –с и с.
Т.е. y = kx + b
f ( c ) f ( c )
2c = c (f(-c) + f(c))
c f ( x ) dx
2
c
(площадь трапеции (а + b)/2 h)
y = f(x)
y
-c
0
c
x
4.
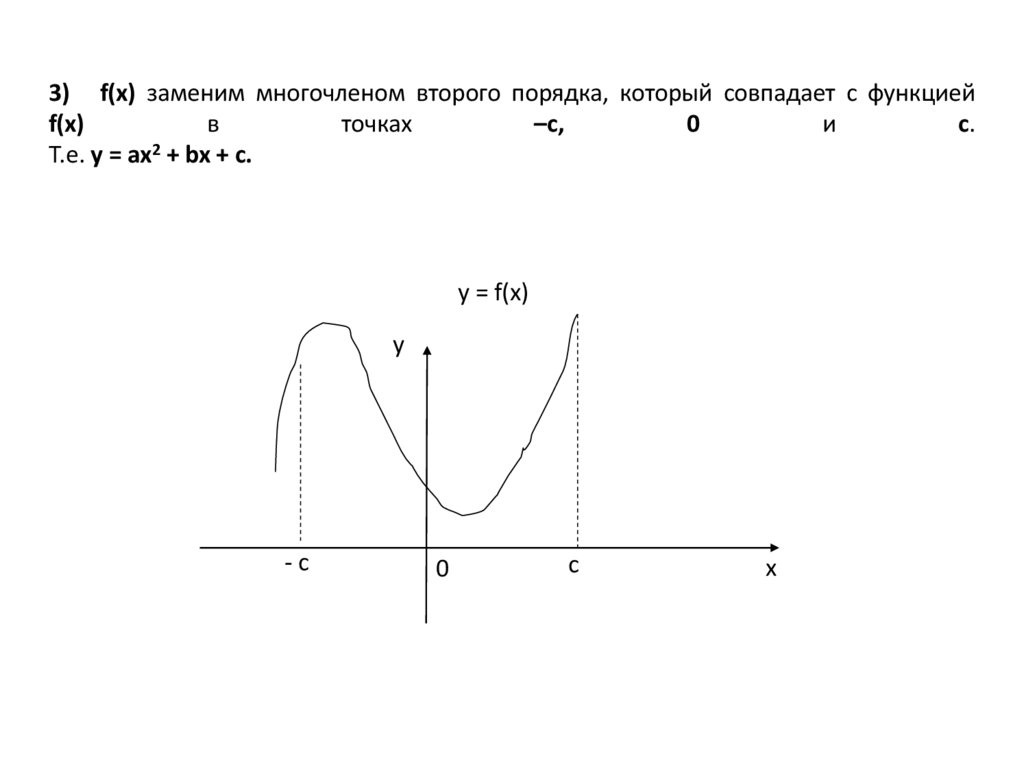
3) f(x) заменим многочленом второго порядка, который совпадает с функциейf(x)
в
точках
–с,
0
и
с.
Т.е. y = ax2 + bx + c.
y = f(x)
y
-c
0
c
x
5.
1.Метод прямоугольников
b
Пусть дан интеграл
f ( x ) dx
a
Отрезок интегрирования [a, b] разобьем на n равных частей: a = x0 < x1 < x2 <
x3 <…< xn = b, тогда длина каждого отрезка
b a
h
n
, xk = x0 + kh.
Формулы прямоугольников имеют вид:
b a
a f ( x ) dx n (f(x0 ) + f(x1 ) + f(x2 ) +…+ f(xn-1 )) + Rn
b
или
b a
a f ( x ) dx n (f(x1 ) + f(x2 ) + f(x3 ) +…+ f(xn )) + Rn
b
6.
Однако для удобства вычислений поступают следующим образом:Точку x1 выбирают таким образом, чтобы она являлась серединой первого
отрезка, т.е. при разбивании отрезка на части таким образом:
a = x0 < x2 < x4 < x6 <…< x2n = b, точка
x0 x1
x1 =
2
Остальные точки получаются прибавлением шага h к каждой предыдущей
точке. В результате получается формула:
b a
a f ( x ) dx n (f(x1 ) + f(x3 ) + f(x5 ) +…+ f(x2n-1 )) + Rn
b
– обобщенная формула прямоугольников.
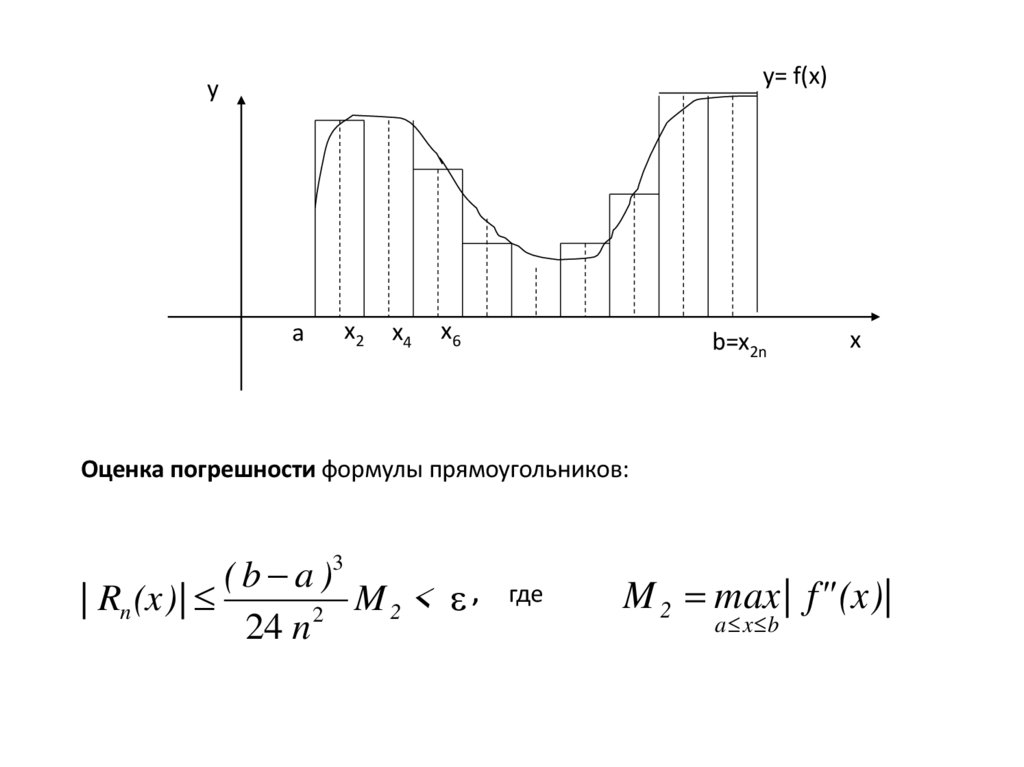
7.
y= f(x)y
a
x2
x4
x6
b=x2n
x
Оценка погрешности формулы прямоугольников:
( b a )3
,
| Rn (x) |
M
<
2
24 n 2
где
M 2 max | f" (x)|
a x b
8.
2.Метод трапеций
b
f (x) dx
Пусть дан интеграл
a
Отрезок интегрирования [a, b] разобьем на n равных частей: a = x0 < x1 < x2 <
x3 <…< xn = b, тогда длина каждого отрезка
b a , x = x + kh.
k
0
h
n
f ( xk ) f ( xk 1 )
f ( x )dx
h
a f ( x ) dx
2
k 0 xk
k 0
b
n 1 xk 1
n 1
b a
{ f(x0 ) + f(x1 ) + f(x1 ) + f(x2 ) + f(x2 ) + f(x3 ) + f(x3 ) +…+ f(xn-1 ) + f(xn )} =
2n
n 1
b a
{f(a) + f(b) + 2 f ( xk ) }
2n
k 1
9.
Вывод:n 1
b a
f ( xk ) }
a f ( x ) dx 2n {f(a) + f(b)+ 2
k 1
b
– формула трапеций.
Оценка погрешности формулы трапеций.
( b a )3
,
| Rn (x) |
M
2
12 n 2
где
M 2 max | f" (x)|
a x b
10.
3) Метод парабол (Симпсона).b
f (x) dx
Пусть дан интеграл
a
Отрезок интегрирования [a, b] разобьем на 2n равных частей: a = x0 < x1 < x2 < x3
<…< x2n = b.
Заменим функцию f(x) на [x0, x2] интерполяционным многочленом Ньютона с
узлами x0, x1, x2.
P2(x) = y0 +
y
h
(x – x0)0+
2 y 0
(x – x )(x – x )
2!h 2
0
1
Где (x – x1) = x – x0 – h
Тогда
(x – x0)(x – x1) = (x – x0)( x – x0 – h) =
=(x – x0)2 – h(x – x0)
11.
x2x2
f ( x) dx P ( x) dx
2
x0
x0
y0
2 y0
2
{ y0
(x - x0 ) 2 [(x - x0 ) - h(x - x0 )] } dx
h
2!h
x0
x2
x2
y 0 ( x x0 ) y 0 ( x x 0 ) y 0 ( x x 0 )
y0 x
2
h
2
3
2!h
2 x
2!h
0
2
2
3
2
2
y0 ( x2 x0 ) 2 2 y0 ( x2 x0 ) 3 2 y0 ( x2 x0 ) 2
y0 (x 2 - x0 )
2
h
2
3
2!h
2
2!h
12.
y 0 ( 2 h ) y 0 ( 2h ) y 0 ( 2 h ) 2y0 2h
2
h
2
2!h 2
2!h 3
2
2
3
= 2h y0 + 2h y0 +
4
h 2y0 – 2y0 h =
3
= h (2y0 +2(y1 – y0) +
1
(y2 – 2y1 + y0)) =
3
1
= h ( y2 +
3
2
h
4
1
y1 + y0) = ( y2 + 4y1 + y0)
3
3
3
x2
h
x f ( x) dx 3 (y2 4y1 y0 )
0
тогда на промежутке [x0, x2] имеем:
13.
x4h
x f ( x) dx 3 (y4 4y3 y2 )
2
b
b
f ( x) dx P ( x) dx
2
a
a
h ( y + 4y + y + y + 4y + y + y + 4y + y + … + 4y + y ) =
2
1
0
4
3
2
6
5
4
2n–1
2n–2
3
n
n 1
=
h
{f(a) + f(b)+ 2
f ( x 2+k4)
3
k 1
}
f (x
k 1
2 k 1
)
14.
Вывод:b a
a f ( x) dx 6n {f(a) + f(b)+ 2
b
n 1
n
+f4( x ) } f ( x
2k
k 1
Оценка погрешности формулы парабол:
(b a)
| Rn (x)|
M4
4
180 (2n)
5
где
M 4 max | f
a x b
IV
(x)|
k 1
2 k 1
)
15. §2. Формулы Ньютона-Котеса
bf ( x)dx
Необходимо вычислить
a
Делим отрезок [a, b] на n равных частей.
Шаг разбиения
Тогда
b a
h
и x0 = a,
n x i = x i –1 + h (i=1,2,…,n–1), xn= b.
b
n
f ( x)dx (b - a) Hi yi
(1)
i 0
a
– квадратурная формула Ньютона-Котеса,
n i
где
1 ( 1)
q(q 1) (q n)
H i :
dq
n i!(n i)! 0
q i
n
(2)
– коэффициенты Котеса.
(значению x = a, соответствует значение q = 0, а x = b – значение q = n и dx =
hdq)
16.
Эти формулы определяют семейство квадратурных формул.Параметром этого семейства является число n – степень интерполяционного
многочлена, которым заменяется подынтегральная функция.
Рассмотрим несколько простейших
небольшим значениям n N.
частных
случаев,
соответствующих
При этом конкретные формулы будем получать не на основе общих формул, а
используя для этой цели вместо многочлена Лагранжа
( 1) n i yi q(q 1)...(q n)
Ln (x0 qh)
q i
i 0 i!(n i )!
n
Эквивалентный ему первый интерполяционный многочлен Ньютона:
17.
q (q 1)2
Pn(x0 + qh) = y0 + q y0 +
2! y0 + … +
q (+q 1)...( q n 1)
n!
1.
ny0
(3)
Пусть n=1, т.е. имеется всего две точки x0 и x1=x0 + h, в которых известны
значения
функции
(y0
=
f(x0)
и
y1 = f(x1))
Этим точкам соответствуют значения 0 и 1 переменной q.
Следовательно
x1
1
q
x f ( x)dx 0 ( y0 q y0 ) h dq h y0 q 2 y0
0
0
1
y1 y 0 h y0 y1
h y0
2
2
2
(4)
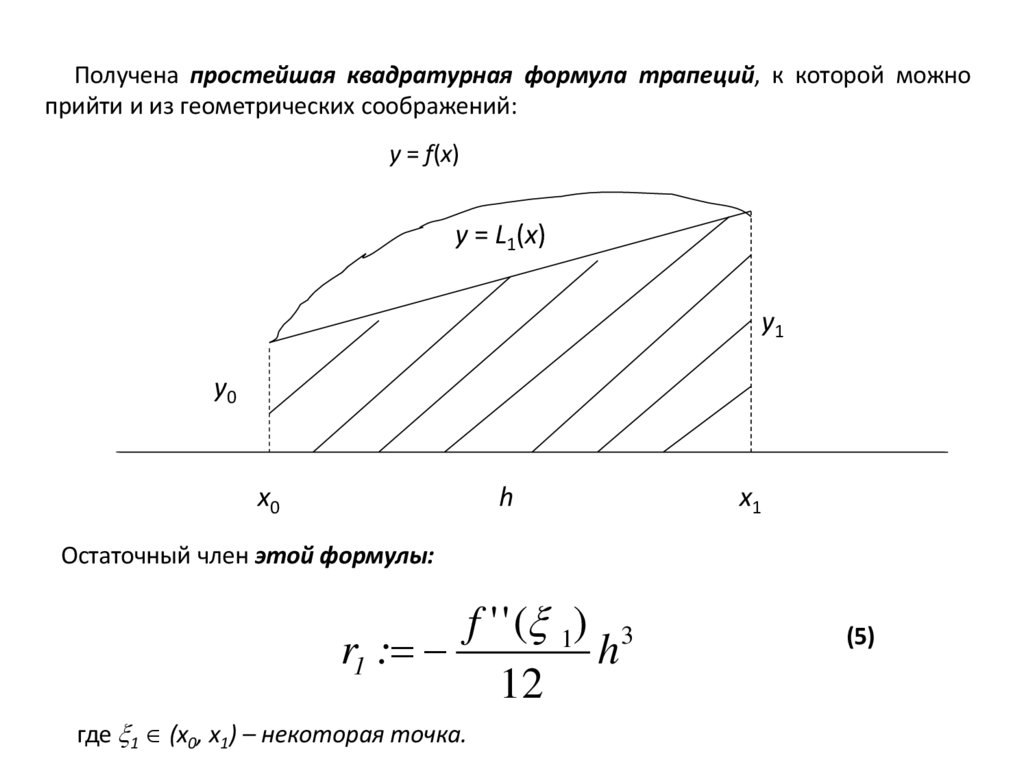
18.
Получена простейшая квадратурная формула трапеций, к которой можноприйти и из геометрических соображений:
y = f(x)
y = L1(x)
y1
y0
x0
h
x1
Остаточный член этой формулы:
f ' ' ( 1) 3
r1 :
h
12
где 1 (x0, x1) – некоторая точка.
(5)
19.
2.Положим в (3) n = 2, т.е. проинтерполируем функцию f(x) по трем точкам: x0, x1
= x0 + h, x2 = x0 = 2h.
Тогда
q (q 1) 2
x f ( x)dx 0 ( y0 q y0 2 y0 ) h dq
0
x2
2
1
= h [ 2y0 + 2(y1 – y0) + (y2 – 2y1 + y0)] =
3
h
=
(y + 4y + y )
3
0
1
2
(6)
Полученное приближенное равенство называется простейшей формулой
Симпсона.
Ее остаточный член:
h5 IV
r2 :
f ( ), (x0, x2)
90
(7)
20.
3.Предполагая теперь n = k, мы придем к частным формулам Ньютона-Котеса:
xk
k
(k )
f
(
x
)
dx
B
h
a
f ( xi ) rk (h)
k i
x0
(6)
i 0
(k )
a
где xi = x0 + ih, а коэффициенты Bk, i , и остаточные члены rk(h) задаются таблицей
(точка (x0,xk), для каждого k своя).
21.
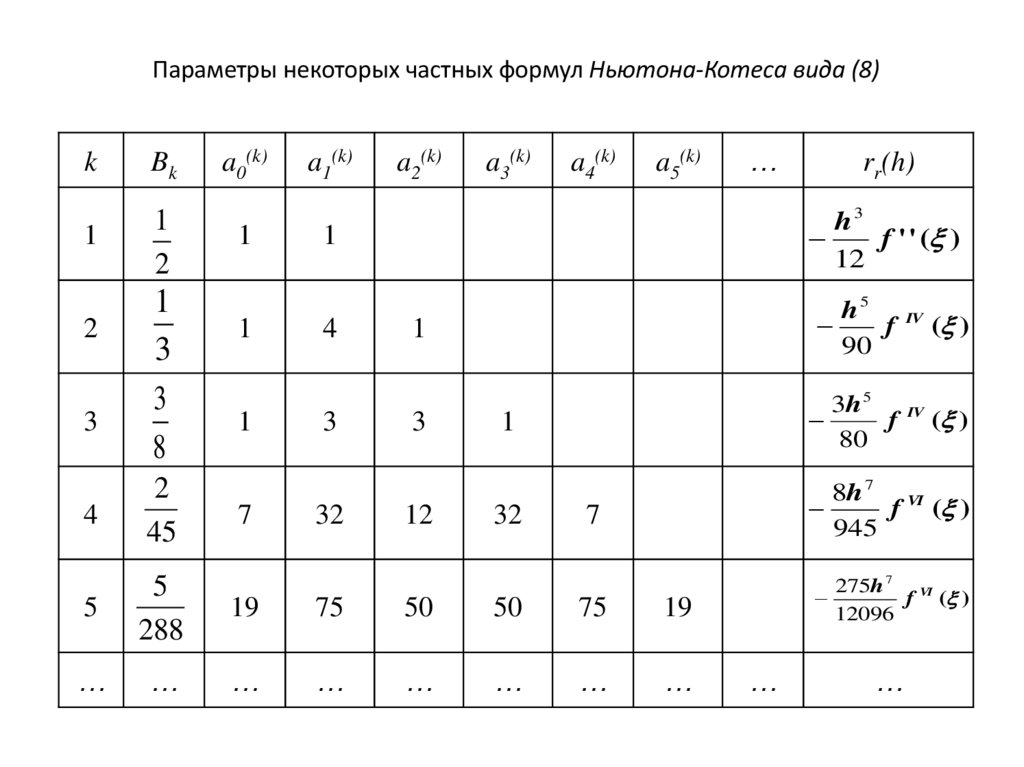
Параметры некоторых частных формул Ньютона-Котеса вида (8)k
Bk
1
1
2
2
3
1
3
3
8
a0(k)
1
1
1
a1(k)
a2(k)
a3(k)
a4(k)
a5(k)
rr(h)
1
h3
f ' ' ( )
12
4
1
h 5 IV
f ( )
90
3
1
3h 5 IV
f ( )
80
32
7
8h 7 VI
f ( )
945
275h 7 VI
f ( )
12096
3
4
2
45
5
5
288
19
75
50
50
75
19
…
…
…
…
…
…
…
…
7
…
32
12
…
…






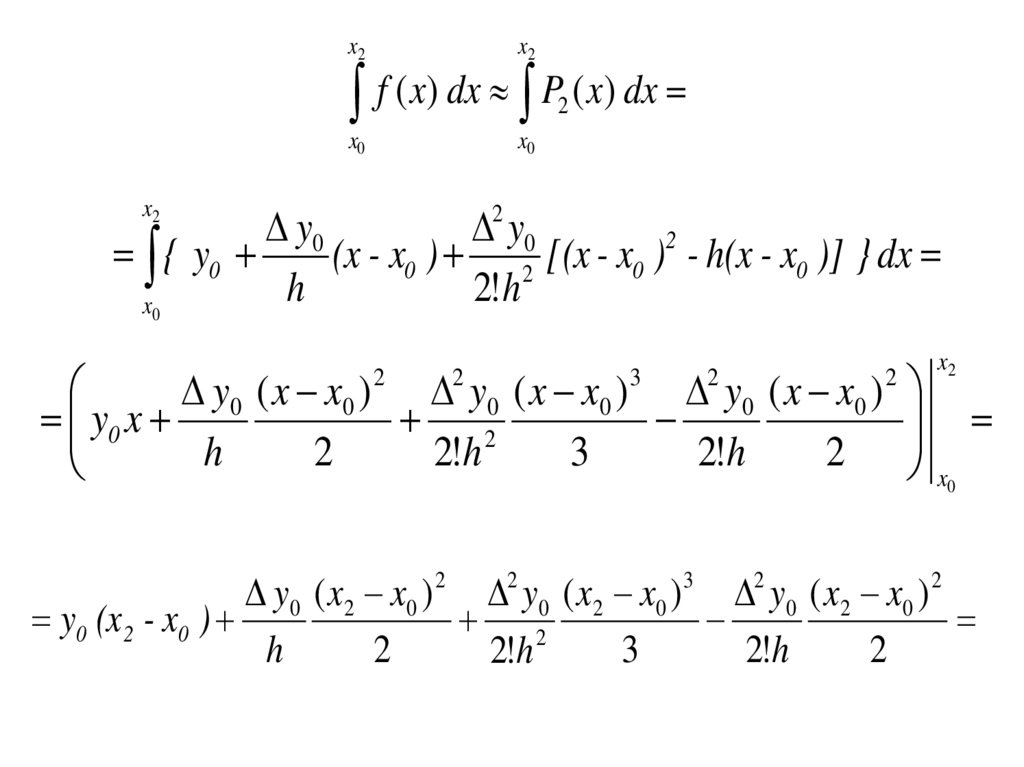
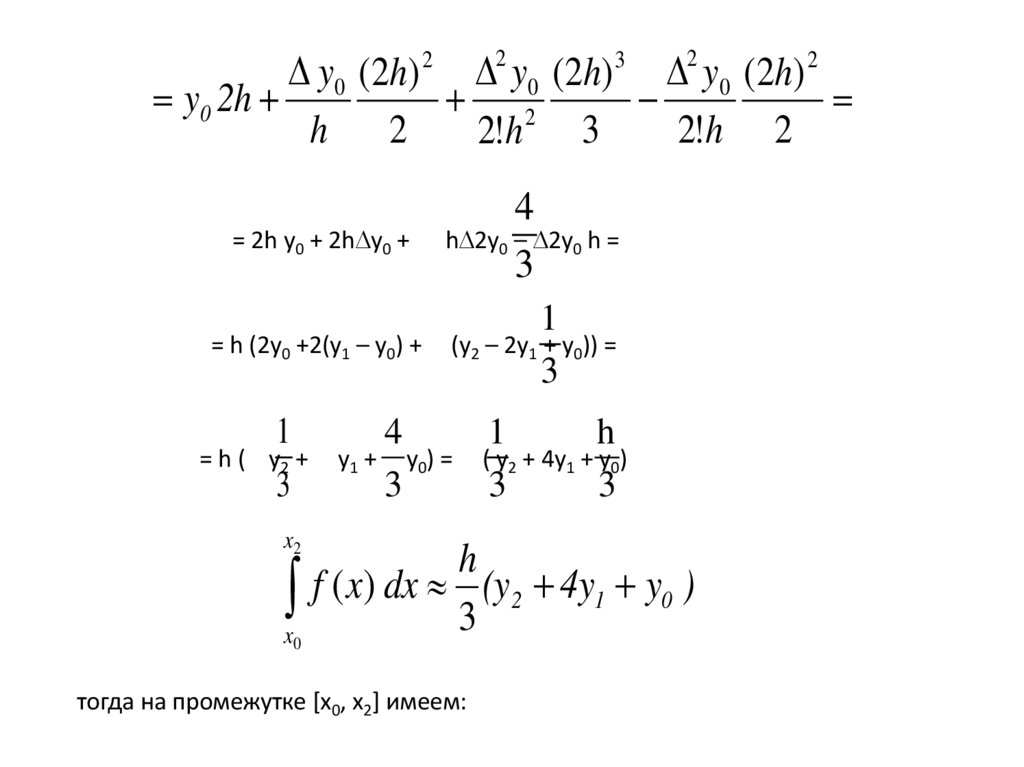
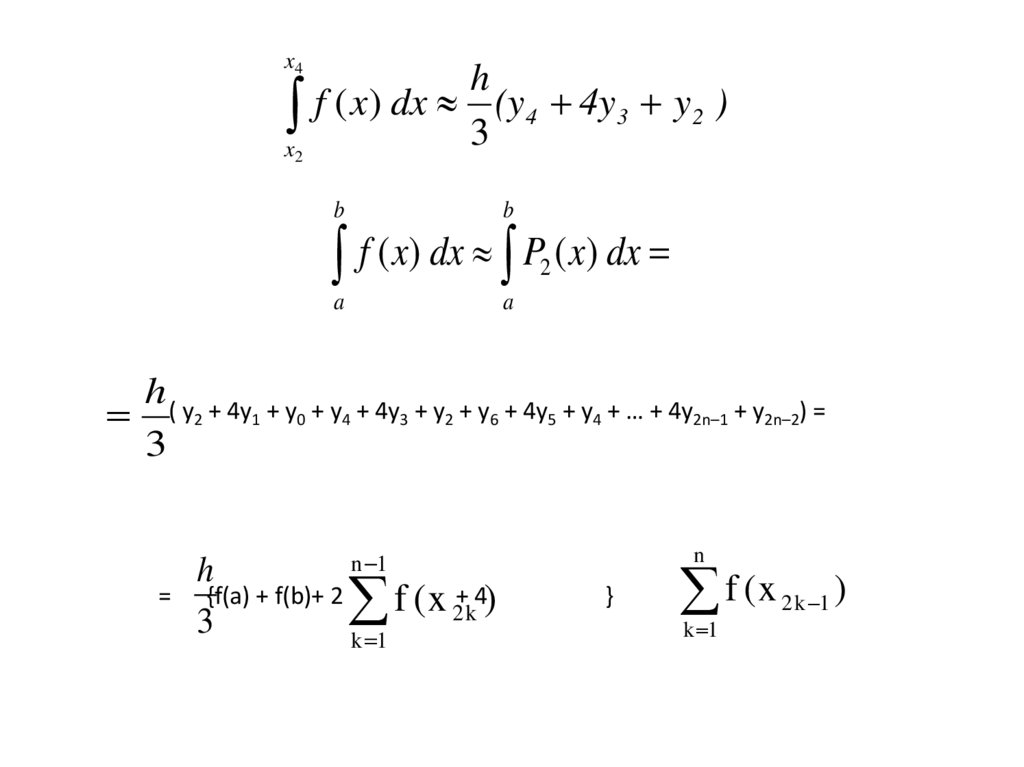






 Математика
Математика








