тригонометрия

1. Тема урока:

”Основные понятия тригонометрии:
радианная мера угла, вращательное
движение, синус, косинус, тангенс,
котангенс угла”

2.

Что такое тригонометрия?
Тригономе́трия (от др.греч. τρίγωνον «треугольник»
и μετρέω «измеряю») — раздел математики, в
котором изучаются тригонометрические
функции и их использование в геометрии.
Данный термин впервые появился в 1595 г. как
название книги немецкого
математика Бартоломеуса Питискуса, а сама
наука ещё в глубокой древности
использовалась для расчётов в астрономии,
архитектуре и геодезии для вычисления одних
элементов треугольника по данным о других
его элементах.

3.

Рассмотрим окружность радиуса R
и отметим на ней дугу РМ длины R и
угол РОМ.
Центральный угол, опирающийся на дугу, длина которой
равна радиусу окружности, называется углом в один радиан.
Градусная мера угла в 1 радиан равна:
Так как π = 3,14, то 1 рад ≈57,3°.
Если угол содержит а радиан, то его градусная мера равна:

4.

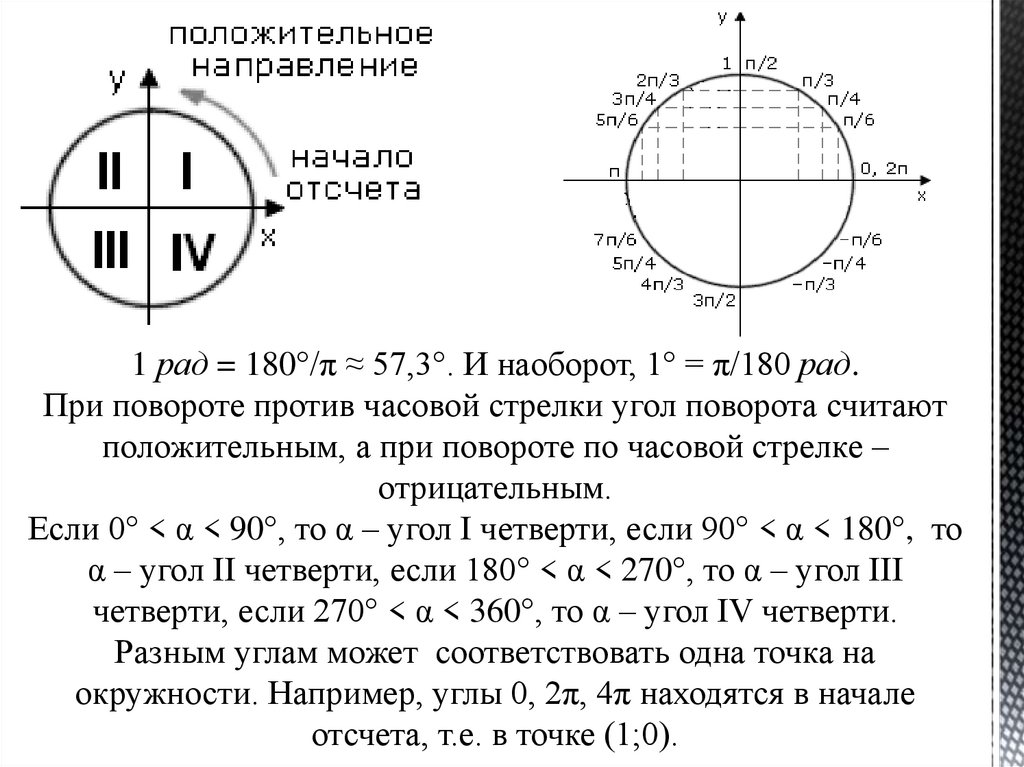
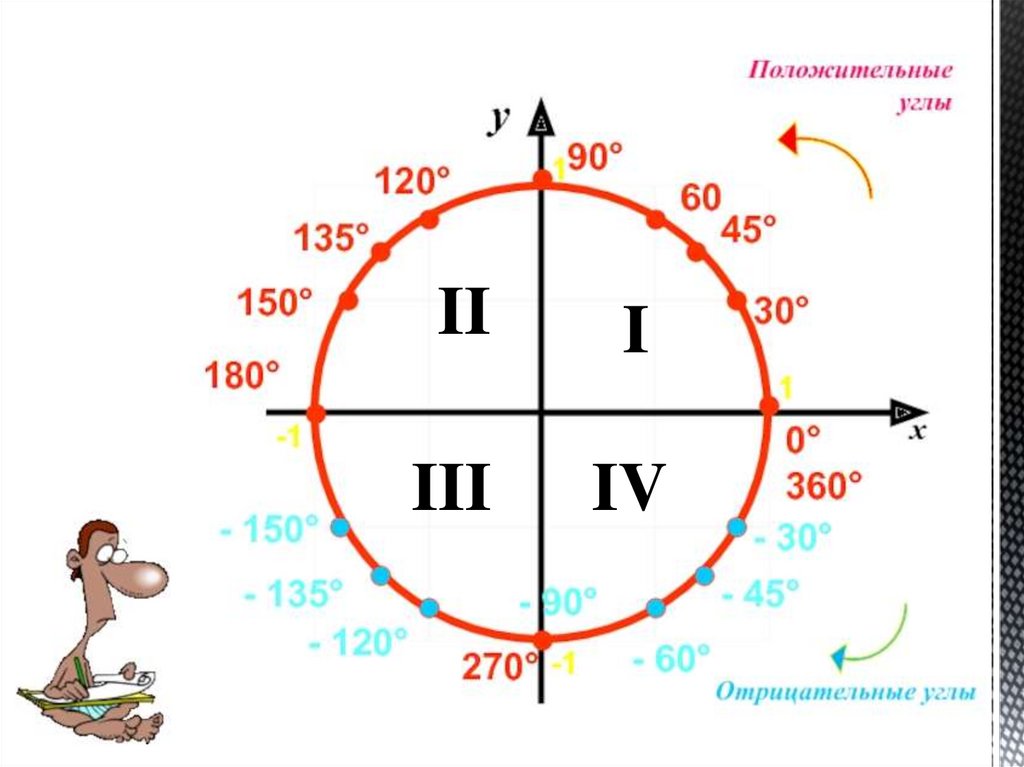
1 рад = 180°/π ≈ 57,3°. И наоборот, 1° = π/180 рад.
При повороте против часовой стрелки угол поворота считают
положительным, а при повороте по часовой стрелке –
отрицательным.
Если 0° < α < 90°, то α – угол I четверти, если 90° < α < 180°, то
α – угол II четверти, если 180° < α < 270°, то α – угол III
четверти, если 270° < α < 360°, то α – угол IV четверти.
Разным углам может соответствовать одна точка на
окружности. Например, углы 0, 2π, 4π находятся в начале
отсчета, т.е. в точке (1;0).

5.

II
I
III
IV

6.

Синусом угла α называется отношение ординаты
точки A к длине отрезка OA. Обозначают
sin α = OC/OA. Так как длина отрезка OA = 1, то
sin α = ОC=у.
Косинусом угла α называется отношение
абсциссы точки A к длине отрезка OA.
Обозначают cos α = OB/OA. Так как длина отрезка
OA = 1, то cos α = OB=х
Тангенсом угла α называется отношение ординаты точки A к абсциссе
точки A. Обозначают tg α = OC/OB. Так как OC = sin α, OB = cos α, то
tg α = sin α/cos α.
Котангенсом угла α называется отношение абсциссы точки A к
ординате точки A. Обозначают ctg α = OB/OC. Так как OC = sin α,
OB = cos α, то ctg α = cos α/sin α.
Котангенс равен обратному значению тангенса: ctg α = 1/tg α.
Из определения следует: если cos α = 0, то тангенс этого угла (α) не
существует. Аналогично для котангенса: если sin α = 0, то котангенс этого
угла (α) не существует.

7.

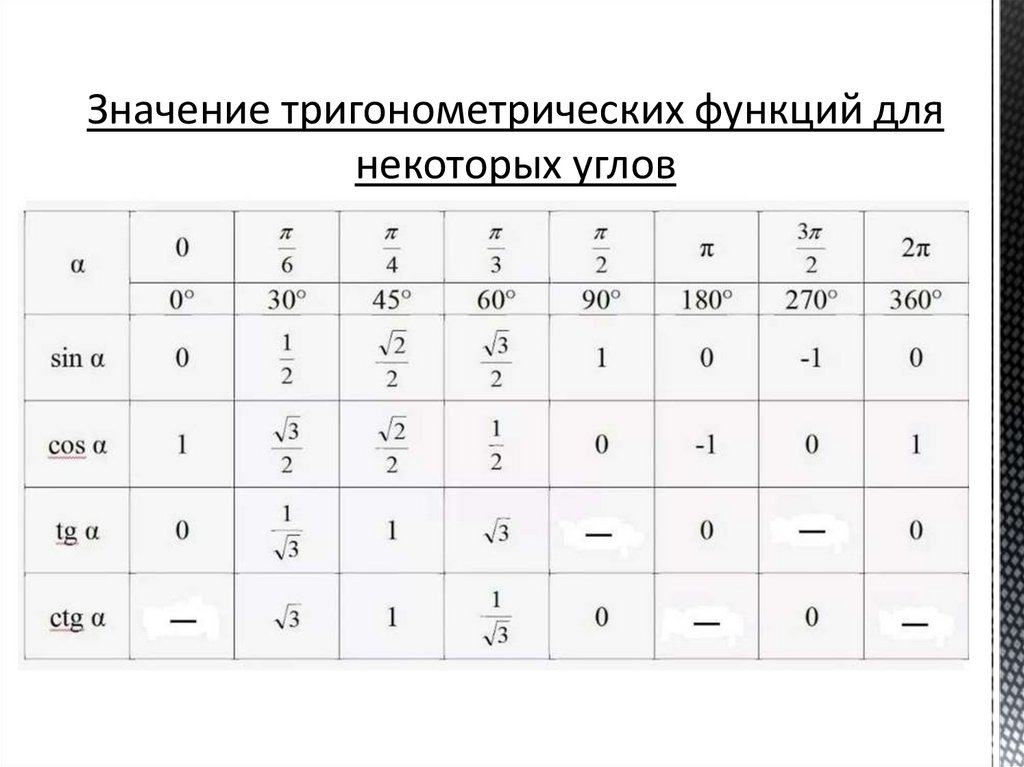
Значение тригонометрических функций для
некоторых углов

8.

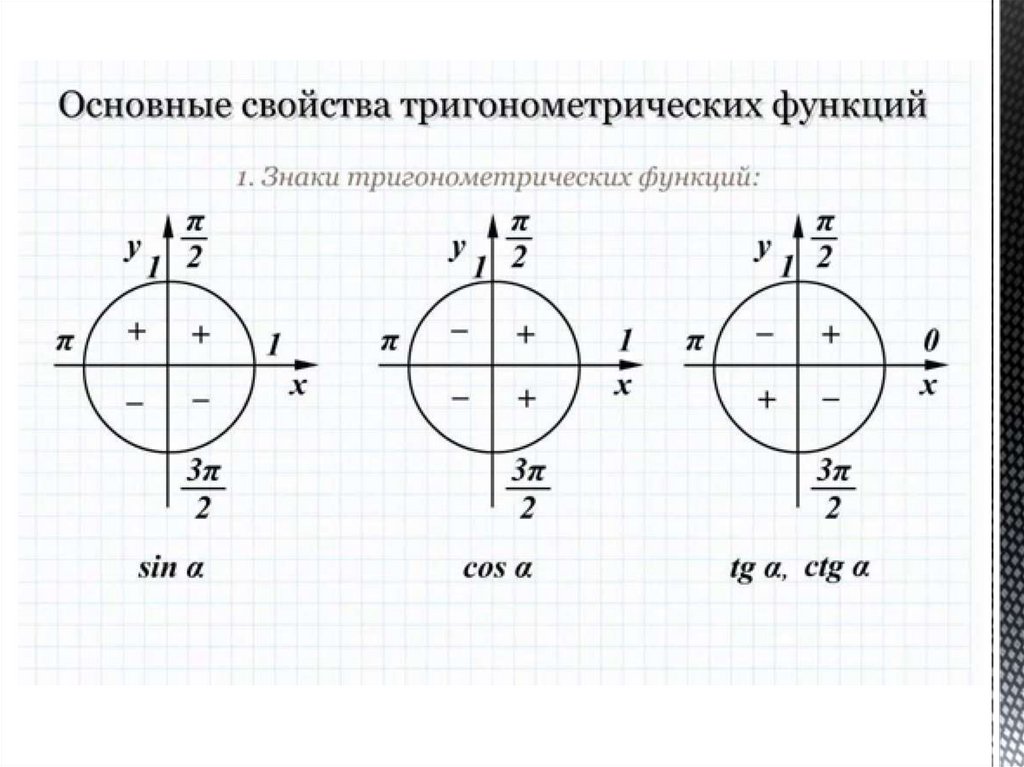
Функция cos является
четной функцией.
Функции: sin, tg, ctg –
нечётные функции.
cos (-x) = cos x;
sin (-x) = - sin x; cos (-300) = cos 300;
0) = - sin 450;
sin
(-45
tg (-x) = - tg x;
0) = - tg 600;
tg
(-60
ctg (-x) = - ctg x.
ctg (-750) = - ctg 750.

9.

10.

Задача 1. Найдите градусную меру угла равного π радиан,
π/2 радиан, 3π/4 рад.
Решение: по формуле:
180
рад
0
π радиан = 1800; π/2 радиан = 900, 3π/4 рад = 1350.
Найдём радианную меру угла в 10. Так как угол 1800 равен π
радиан, то: 0
1
180
рад
Если угол содержит α градусов, то его радианная мера
составляет:
0
180
рад

11.

Задача 2. Найдите радианную меру угла равного 450, 150
Решение:
0
180
45
0
15
0
180
180
45 рад
15 рад
4
12
рад
рад

12.

Площадь кругового сектора радиуса R, образованного
углом в π рад, равна:
R2
S
, где 0
2
Длина дуги, радиуса R, стягиваемая центральным углом α,
вычисляется по формуле:

13.

.
Задача 3. Найти радианную меру угла, выраженного в
градусах: 1) 40°; 2) 120°; 3) 150°
Задача 4. Найти градусную меру угла, выраженного в
радианах: 3
; ;2;3;0,36
6 9 4
;

14.

Задача 5. Вычислить радиус окружности, если дуга
длиной 0,36 м стягивает центральный угол в 0,9 рад.
Задача 6. Найти радианную меру угла, стягиваемого дугой
окружности длиной 3 см, если радиус окружности равен 1,5
см.

15.

Задача 7. Дуга кругового сектора стягивает угол в 3π/4
рад. Найти площадь сектора, если радиус круга равен 1 см.
Задача 10. Определите в какой четверти заключается угол α,
если: а) α = 1200; б) α = 4350; в) α = - 2800
Домашнее задание: Найдите значение выражения: