Похожие презентации:
Презентация лекции 11 Треуг элемент
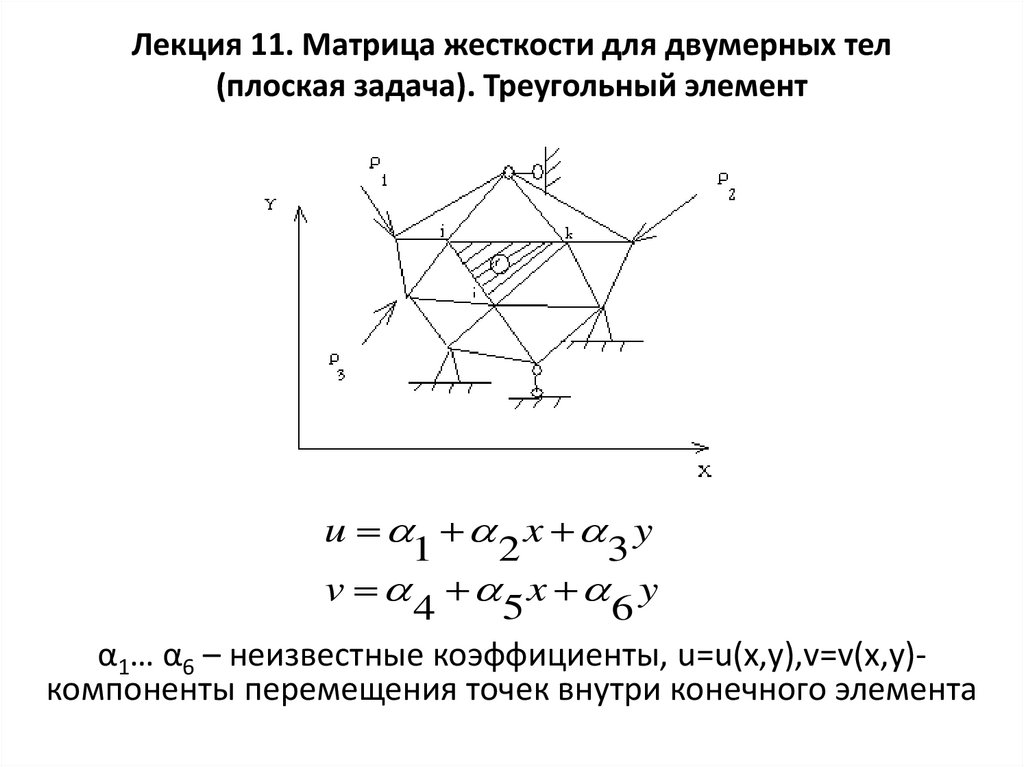
1. Лекция 11. Матрица жесткости для двумерных тел (плоская задача). Треугольный элемент
u x y1
2
3
v x y
5
4
6
α1… α6 – неизвестные коэффициенты, u=u(x,y),v=v(x,y)компоненты перемещения точек внутри конечного элемента
2. Связь коэффициентов α1… α6 с узловыми перемещениями
z1z2
z r z3
z
4
z5
z 6
ui 1
vi 0
z r u j 1
v 0
j
u 1
k
v 0
k
r
z H ,
xi
0
xj
yi 0
0 1
yj 0
0
0
x
k
0
0
xi
0
1 xj
y 0 0
k
0 1 x
k
0
1
yi
2
0
3
y j
4
0 5
y 6
k
1
r
H z
3. Компоненты перемещения внутри элемента
1u (ai bi x ci y)ui (a j b j x c j y)u j (a b x c y)u
k k
k k
2
v
1
(
a
b
x
c
y
)
v
(
a
b
x
c
y
)
v
(
a
b
x
c
y
)
v
i i
j j
j j
k k
k k
2 i i
ai xi y x yi ,
k k
1 xi
1
1 xj
2
1 x
k
yi
yj
y
k
bi y j y ,
k
ci x x j
k
4. Путем перестановки индексов i,j,k определяются все коэффициенты aj,bj,cj, ak,bk,ck,
5. Связь деформаций с узловыми перемещениями
u uvT
r
L z ,
u 1
x (bi ui b j u j b u ),
k k
x 2
v 1
y (ci vi c j v j c v ),
k k
y 2
u v 1
xy (ci ui c j u j c u bi vi b j v j b vk )
k k
k
y x 2
6. Деформации для r-го элемента
bi
x
1
r
y
0
2
c
xy
i
b
i
1
r
B
0
2
c
i
0
ci
bi
bj
0
0
cj
b
k
0
cj
bj
c
k
0
bj
0
ci
bi
o
cj
b
k
0
cj
bj
c
k
0
c
k
b
k
0
r
r
r
c z B z .
k
b
k
7. Закон Гука для плоской задачи
1x
E
y
1 2
0
xy
1
0
D ,
1
E
D
2
1
0
1
0
0
0
1
2
0 x
0 y ,
1
xy
2
8.
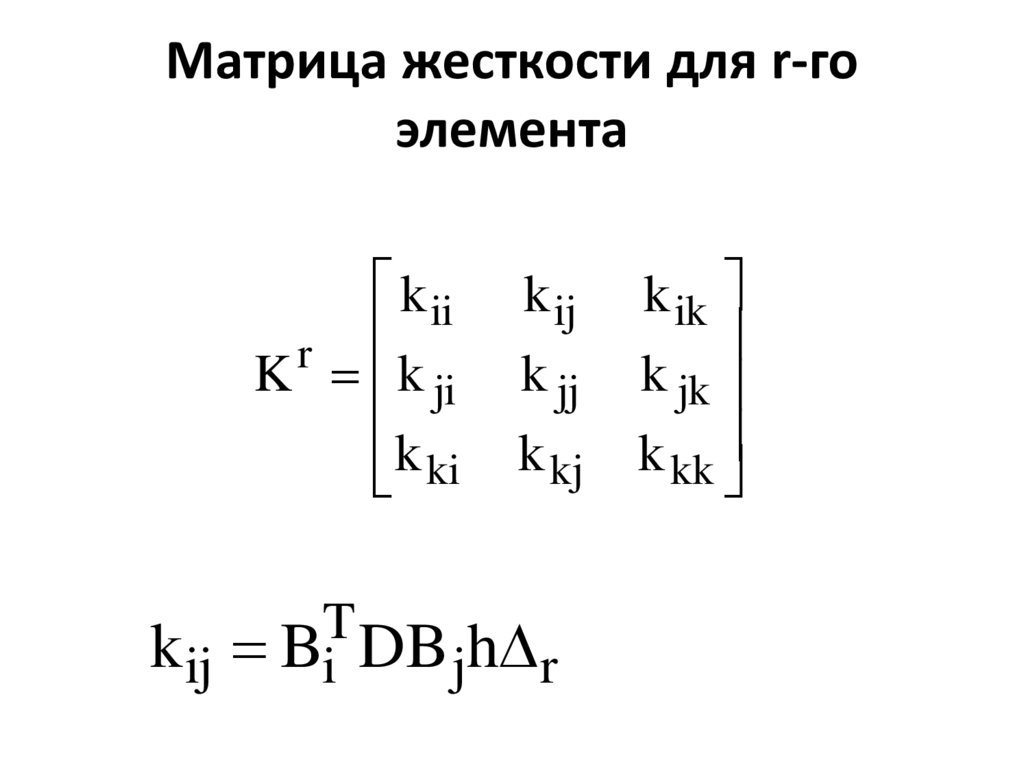
9. Матрица жесткости для r-го элемента
k iir
K k ji
k ki
k ij
k jj
k kj
T
k ij Bi DB jh r
k ik
k jk
k kk
10.
11. Выражения перемещений внутри элемента через компоненты узловых перемещений
• ui , uj , uk –перемещения узловых точек в направлении оси х• vi , vj , vk -перемещения узловых точек в направлении оси у
оси х
12. Выражения для перемещений произвольного треугольного элемента
u1
(
a
b
x
c
y
)
u
(
a
b
x
c
y
)
u
(
a
b
x
c
y
)
u
i i
j
j
j
j
k k
k
k
2 i i
v
1
(
a
b
x
c
y
)
v
(
a
b
x
c
y
)
v
(
a
b
x
c
y
)
v
i i
j
j
j
j
k k
k k
2 i i
ai xi y x yi ,
k
k
1 xi
1
1 xj
2
1 x
k
yi
yj
y
k
bi y j y ,
k
ci x x j
k
13. Тестовые вопросы
1. Компонентыперемещения
внутри
элемента для плоского элемента
2. Физические уравнения
3. Выражения
перемещений
внутри
элемента через компоненты узловых
перемещений
4. Степень свободы КЭ






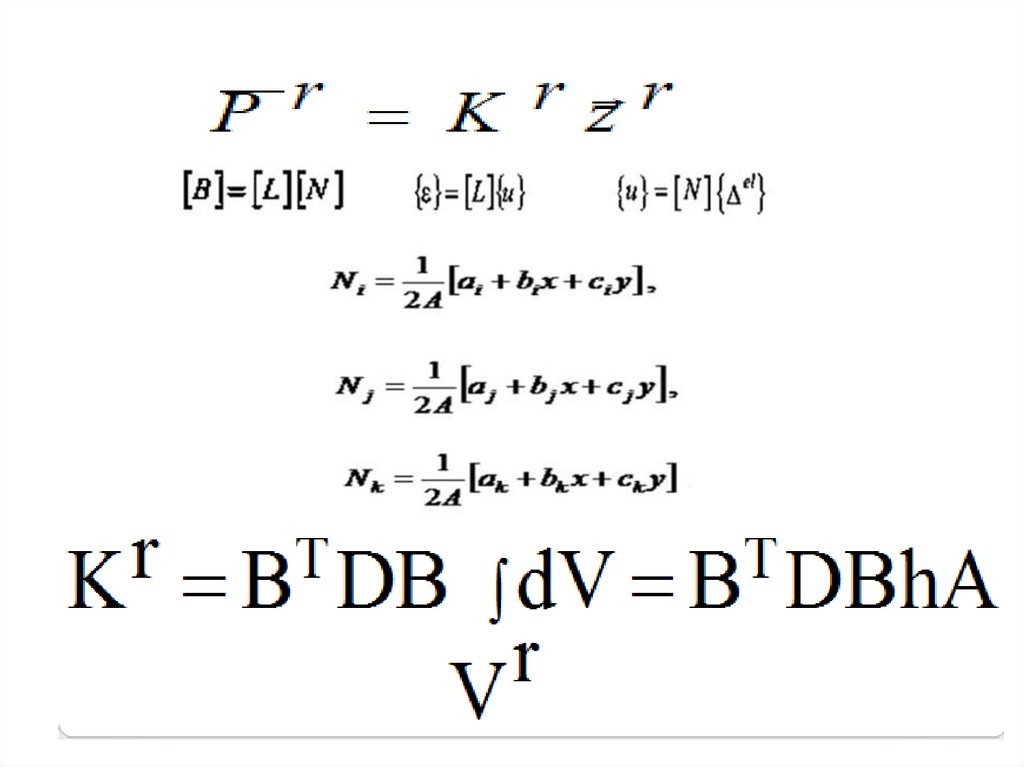
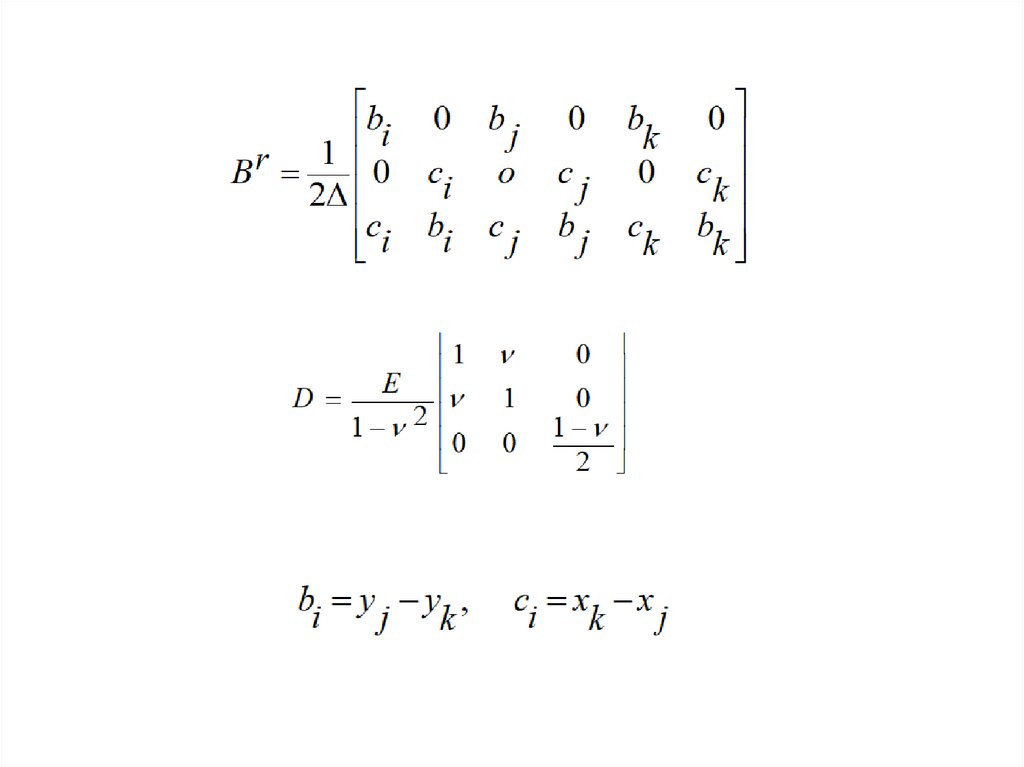


 Математика
Математика








