Тема 4. Аппроксимация

1.

Андреева Анна Дмитриевна

2. Постановка задачи аппроксимации функций

xi a, b , i 0, n ( x0 a, xn b)
f ( xi ), i 0, n
узлы аппроксимации
Задача аппроксимации функции:
заменить (аппроксимировать) функцию f(x), заданную таблицей
значений, функцией φ(x) так, чтобы отклонение φ(x) от f(x) в
любой точке отрезка [a,b] было наименьшим
Задача интерполирования функции:
заменить (аппроксимировать) функцию f(x) функцией φ(x) так,
чтобы φ(x) совпадала с функцией f(x) в заданных точках (в узлах)
Задача приближения функции:
заменить (аппроксимировать) функцию f(x) функцией φ(x) так,
чтобы φ(x) мало отличалась от f(x) в заданных точках (в узлах)

3.

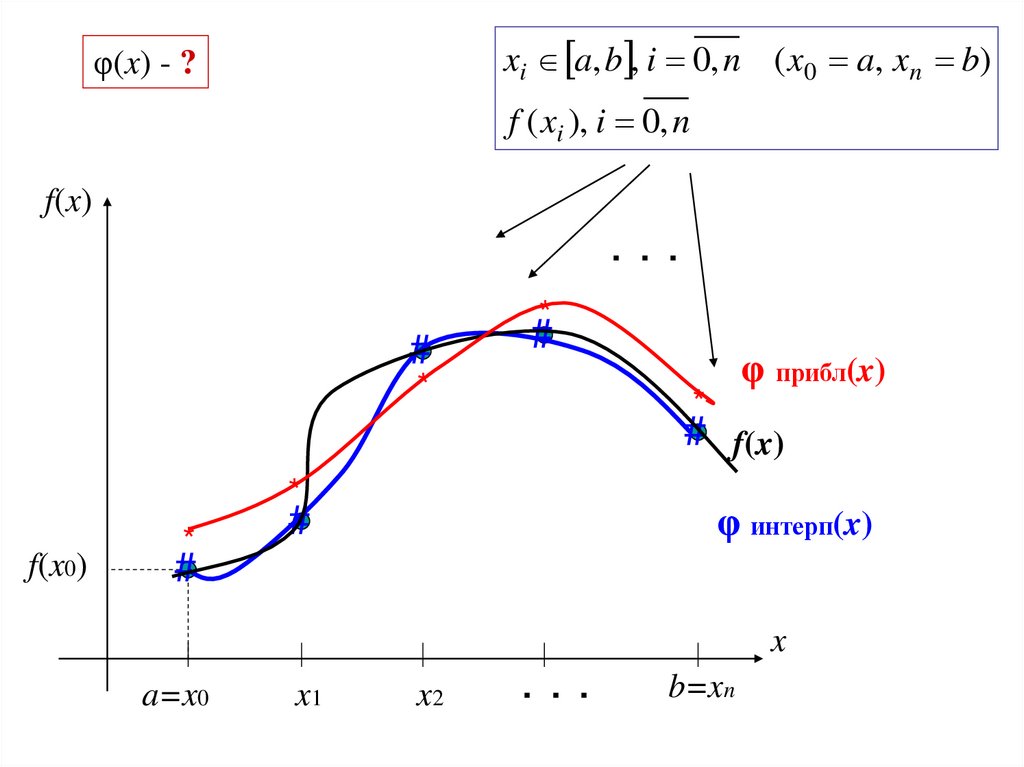
xi a, b , i 0, n ( x0 a, xn b)
φ(x) - ?
f ( xi ), i 0, n
f(x)
. . .
*
#
#
*
φ прибл(x)
*
# f(x)
*
f(x0)
*
φ интерп(x)
#
#
x
a=x0
x1
x2
. . .
b=xn

4. Интерполирование алгебраическими многочленами

xi a, b , i 0, n ( x0 a, xn b)
f ( xi ), i 0, n
n ( x) a0 a1 x a2 x 2 an x n
n ( xi ) f ( xi ), i 0, n
1
2
a0 a1xi a2 xi2 an xin f ( xi ), i 0, n
1 x0 x02 x0n
1 x1 x12 x1n ≠ 0, если среди узлов интерполирования
W
нет совпадающих
1 xn xn2 xnn

5. Интерполяционный многочлен Лагранжа

k n
Ln ( x) C k ( x) f ( xk ) 3
k 0
4
0, i k
Ck ( xi )
1, i k ; i 0, n
k n
Ck ( xi ) f ( xk ) f ( xi ), i 0, n
k 0
x xk :
k
Ck ( x) k ( x x0 )( x x1 ) ( x xk 1 )( x xk 1 ) ( x xn )
5
1
( xk x0 )( xk x1 ) ( xk xk 1 )( xk xk 1 ) ( xk xn )
j n
j n
(x x j )
(x x j )
C k ( x)
j 0,
j k
j n
k n
Ln ( x)
( xk x j )
j 0,
j k
k 0
6
j 0,
j k
j n
( xk x j )
j 0,
j k
f ( xk )

6. Интерполяционные формулы Ньютона

1. Для равноотстоящих узлов
h xi xi 1 const , i 1, n
Конечные разности:
- первого порядка
- второго порядка
f 0 f ( x1 ) f ( x0 ),
2 f 0 f1 f 0
, f ( x2 ) 2 f ( x1 ) f ( x0 )
f1 f ( x2 ) f ( x1 ),
f n 1 f ( xn ) f ( xn 1 )
- k-го порядка
k f i k 1 f i 1 k 1 f i , i 0, n k ;
k 1, n
k f i f ( xk i ) k f ( xk i 1 )
k (k 1)
f ( xk i 2 ) ( 1) k f ( xi )
2!

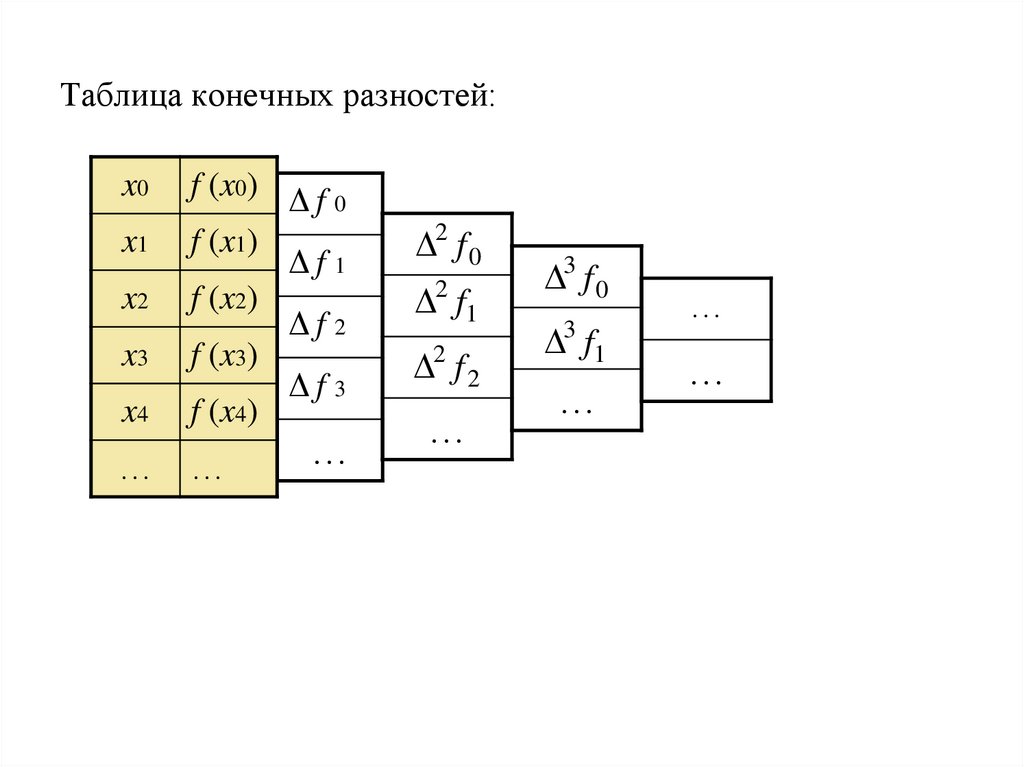
7. Таблица конечных разностей:

x0
x4
f (x0) Δ f 0
f (x1)
Δf1
f (x2)
Δf2
f (x3)
Δf3
f (x4)
…
…
x1
x2
x3
…
2 f 0
2 f1
2 f 2
…
3 f 0
3 f1
…
…
…

8. Формирование многочлена Ньютона для равноотстоящих узлов

7
( x) N ( x) a0 a1 ( x x0 ) a2 ( x x0 )( x x1 ) an ( x x0 )( x x1 ) ( x xn 1 )
n ( xi ) f ( xi ), i 0, n
N ( x0 ) a0 f ( x0 ),
N ( x1 ) a0 a1 ( x1 x0 ) f ( x1 ),
ak
k f 0
k! h
k
f ( x1 ) f ( x0 ) f 0
a1
x1 x0
h
, k 0, n
8
f 0
2 f 0
n f 0
N ( x ) f ( x0 )
( x x0 )
( x x0 )( x x1 )
( x x0 ) ( x xn 1 )
2
n
h
2!h
n!h

9.

2. Для неравноотстоящих узлов
xi xi 1 const , i 1, n
Разделенные разности:
- первого порядка:
- второго
порядка:
f ( xi 1 ) f ( xi )
f ( xi , xi 1 )
, i 0, n 1
xi 1 xi
f ( xi 2 , xi 1 ) f ( xi 1 , xi )
f ( xi , xi 1 , xi 2 )
, i 0, n 2
xi 2 xi
f ( xi 1 , , xi k ) f ( xi , , xi k 1 )
- k-го порядка: f ( xi , xi 1 , , xi k )
,
xi k xi
i 0, n k ; k 1, n

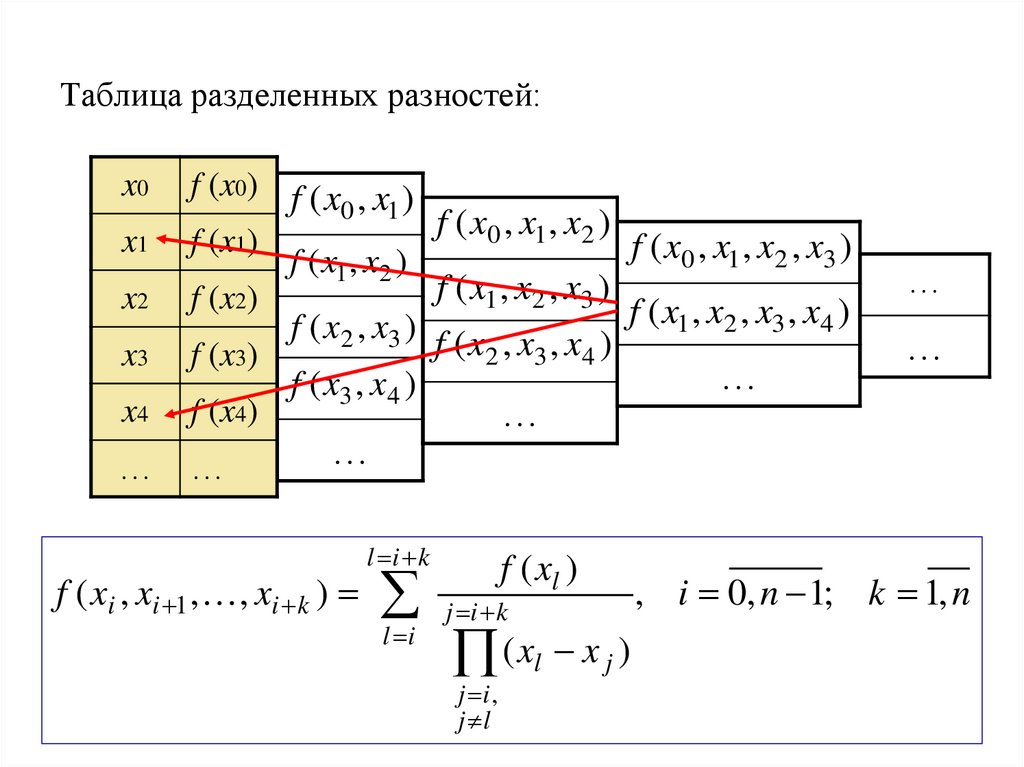
10. Таблица разделенных разностей:

x0
x4
f (x0) f ( x , x )
0 1
f ( x0 , x1 , x2 )
f (x1)
f ( x0 , x1 , x2 , x3 )
f ( x1 , x2 )
f ( x1 , x2 , x3 )
f (x2)
f ( x2 , x3 ) f ( x , x , x ) f ( x1 , x2 , x3 , x4 )
2 3 4
f (x3)
…
f ( x3 , x4 )
f (x4)
…
…
…
x1
x2
x3
…
…
…
l i k
f ( xl )
f ( xi , xi 1 , , xi k ) j i k
l i
( xl x j )
j i ,
j l
, i 0, n 1; k 1, n

11. Формирование многочлена Ньютона для неравноотстоящих узлов

Формирование многочлена Ньютона
7
для неравноотстоящих узлов
( x) P( x) a0 a1 ( x x0 ) a2 ( x x0 )( x x1 ) an ( x x0 )( x x1 ) ( x xn 1 )
n ( xi ) f ( xi ), i 0, n
P( x0 ) a0 f ( x0 ),
P( x1 ) a0 a1 ( x1 x0 ) f ( x1 ),
f ( x1 ) f ( x0 )
a1
f ( x0 , x1 )
x1 x0
ak f ( x0 , x1 , , xk ), k 0, n
9
P( x) f ( x0 ) f ( x0 , x1 )( x x0 ) f ( x0 , x1 , x2 )( x x0 )( x x1 )
f ( x0 , x1 , , xn )( x x0 ) ( x xn 1 )

12.

Замечание 1
При заданном наборе узлов интерполирования существует один
и только один итерполяционный многочлен
Замечание 2
Для более точного расчета значения функции в точке x є [a,b],
x ≠ xi при построении многочлена Ньютона в качестве начальной
точки (x0) следует выбирать узел xi такой, что x ≈ xi
x0
x1
x2
x3
x4
f (x0) Δ f 0
f (x1)
Δf1
f (x2)
Δf2
f (x3)
Δf3
f (x4)
f0
x x2
2
2 f1
2 f 2
3 f 0
3 f1
4 f 0
f 2
2 f 2
N ( x) f ( x2 )
( x x2 )
( x x2 )( x x3 )
2
h
2!h

13.

Многочлены Ньютона для интерполирования назад:
x0
f (x0)
x1
f (x1)
... ...
xn-2 f (xn-2)
xn-1 f (xn-1)
xn
f (xn)
Δf0
Δf1
...
2 f 0
...
Δ f n-2
2 f n 3
Δ f n-1
2 f n 2
3 f 0
...
f n 3
3
…
…
f n 1
2 f n 2
n f 0
N ( x) f ( xn )
( x xn )
( x xn )( x xn 1 )
( x xn ) ( x x1 )
2
n
h
2!h
n!h
P( x) f ( xn ) f ( xn 1 , xn )( x xn ) f ( xn 2 , xn 1 , xn )( x xn )( x xn 1 )
f ( x0 , x1 , , xn )( x xn ) ( x x1 )

14. Погрешность интерполирования

f ( x) n ( x) Rn ( x), x [a, b], x xi , i 0, n
( x x0 )( x x1 ) ( x xn ) ( n 1) *
Rn ( x)
f
(x )
(n 1)!
x* [a, b], x* xi , i 0, n
M n 1 max f ( n 1) ( x)
a x b
10
Rn ( x)
12
( x x0 )( x x1 ) ( x xn )
(n 1)!
M n 1
n ( x ) f ( x )
100 %
f ( x)
M n 1
max Rn ( x)
max ( x x0 )( x x1 ) ( x xn )
(n 1)! x [ a,b]
[ a ,b ]
11

15. Интерполирование с кратными узлами. Многочлен Эрмита

xi a, b , i 0, n ( x0 a, xn b)
f ( xi ), f ( xi ), f ( xi ), , f ( k ) ( xi ); i 0, n; k 0, N i 1
Ni – кратность узла xi
m N 0 N1 N n 1
H m(k ) ( xi ) f (k ) ( xi ), i 0, n; k 0, Ni 1
i n k Ni 1
H m ( x)
i 0
(k )
C
(
x
)
f
( xi )
ik
k 0

16. Тригонометрическая интерполяция

kx
kx
Tn ( x) a0 ak cos
bk sin
T
T
k 1
n
x0 x1 x2 n 1 ,
x2 n 1 x0 T
f ( x0 ), , f ( x2 n 1 )
период функции f ( x)
a0 f ( x0 )
Tn ( x j ) f ( x j ),
j 0,2n 1

17. Интерполирование рациональными функциями

x0 x1 xn ,
kl ( x)
f ( x0 ), , f ( xn )
ak x k ak 1 x k 1 a1 x a0
x bl 1 x
l
kl ( x j ) f ( x j ),
n k l
l 1
b1 x b0
j 0, n

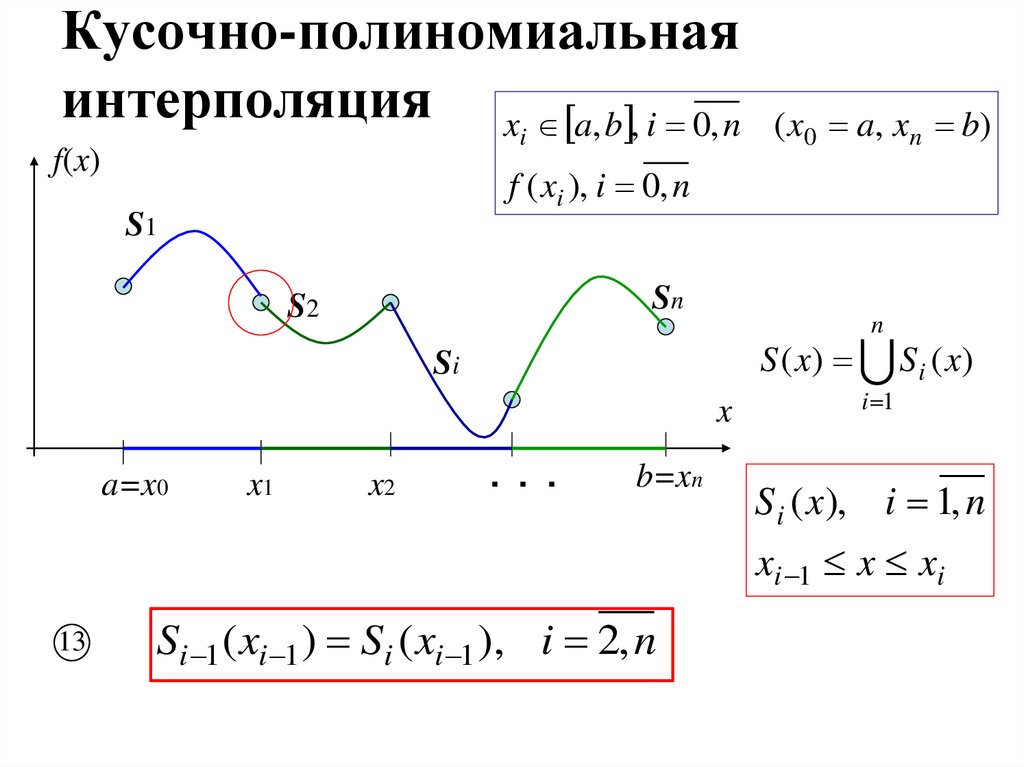
18. Кусочно-полиномиальная интерполяция

xi a, b , i 0, n ( x0 a, xn b)
f(x)
f ( xi ), i 0, n
S1
Sn
S2
n
S ( x) S i ( x)
Si
x
a=x0
x1
x2
. . .
b=xn
i 1
S i ( x), i 1, n
xi 1 x xi
13
Si 1 ( xi 1 ) Si ( xi 1 ), i 2, n

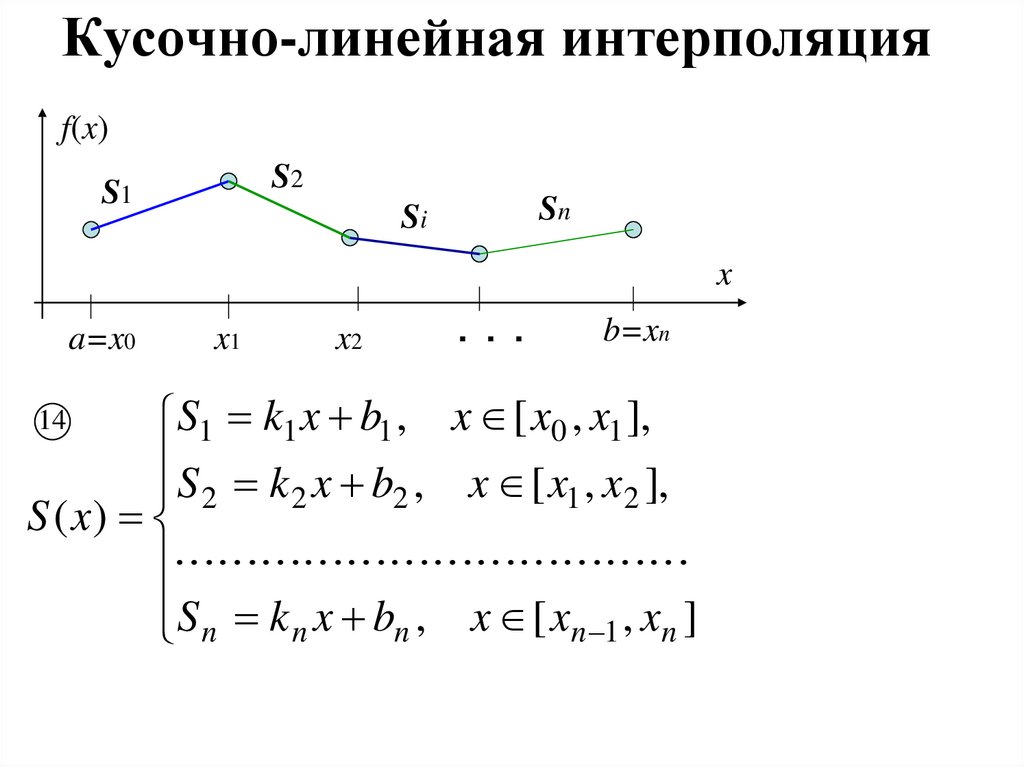
19. Кусочно-линейная интерполяция

f(x)
S2
S1
Sn
Si
x
a=x0
x1
x2
. . .
b=xn
S1 k1 x b1 , x [ x0 , x1 ],
S k x b , x [ x , x ],
2
2
2
1 2
S ( x)
S n k n x bn , x [ xn 1 , xn ]
14

20.

S1 k1 x b1 , x [ x0 , x1 ], S ( xi ) f ( xi ), i 0, n
S k x b , x [ x , x ],
2
2
2
1 2
S ( x)
S n k n x bn , x [ xn 1 , xn ]
k1 x0 b1 f ( x0 )
k1 x1 b1 f ( x1 )
S i 1 ( xi 1 ) S i ( xi 1 ),
k 2 x1 b2 f ( x1 )
i 2, n
k 2 x2 b2 f ( x2 )
k n xn 1 bn f ( xn 1 )
k n xn bn f ( xn )

21. Кусочно-квадратичная интерполяция (параболическая)

Кусочно-квадратичная
f(x)
интерполяция (параболическая)
Si
S ( xi ) f ( xi ), i 0, n
x
. . .
xi-1
xi
xi+1
Si ( x) ai x 2 bi x ci
15
ai xi2 1 bi xi 1 ci f ( xi 1 )
2
ai xi bi xi ci f ( xi )
2
ai xi 1 bi xi 1 ci f ( xi 1 )
. . .
S1 ( x), x [ x0 , x2 ]
S ( x), x [ x , x ]
2 4
S ( x) 2
S m ( x), x [ x2 m 2 , x2 m ]
n 2m

22. Кубический сплайн

Сплайн-функция – кусочно-полиномиальная функция, непрерывная
на отрезке [a,b] и имеющая на этом отрезке несколько непрерывных
производных
xi a, b , i 0, n (a x0 x1 xn b)
hi xi xi 1 const
f ( xi ), i 0, n
Кубический сплайн - функция S(x), удовлетворяющая условиям:
1. На каждом отрезке [xi-1,xi] S(x) – многочлен третьей степени
2. S ( x), S ( x), S ( x) - непрерывны на отрезке [a,b]
3. S ( xi ) f ( xi ), i 0, n
S1
S2
x0
x1
x2
. . .
n
Sn
xn-1
xn
S ( x) S i ( x)
i 1

23. Построение кубического сплайна

16
ci
di
2
S i ( x) ai bi ( x xi ) ( x xi ) ( x xi ) 3
2
6
xi 1 x xi , i 1, n
Смысл неизвестных коэффициентов:
di
S i ( x) bi ci ( x xi ) ( x xi ) 2
2
16.1
16.2
Si ( x) ci d i ( x xi )
16.3
Si ( x) d i
bi S i ( xi ), i 1, n
d i S i ( xi ), i 1, n
i 1
ai f ( xi ), i 0, n
при x = x i
ai S i ( xi ), i 1, n
ci S i ( xi ), i 1, n
Определение коэффициентов ai : n
S ( x) S i ( x)
S ( xi ) f ( xi ), i 0, n
17
4n - ?
Si ( xi ) f ( xi ), i 1, n

24.

Si-1
xi-2
Si 1 ( xi 1 ) Si ( xi 1 ), i 2, n
Si
xi-1
xi
S ( x0 ) f ( x0 ) a0
i 1, n
ai S i ( xi ), i 1, n
bi S i ( xi ), i 1, n
ci S i ( xi ), i 1, n
d i S i ( xi ), i 1, n
Si 1 ( xi 1 ) ai 1
x xi 1 :
ci
di
2
S i ( xi 1 ) ai bi ( xi 1 xi ) ( xi 1 xi ) ( xi 1 xi ) 3
2
6
hi xi xi 1
ci 2 d i 3
bi hi hi hi ai ai 1 f ( xi ) f ( xi 1 ), i 1, n
2
6
18

25.

S i
S i 1
xi-2
xi-1
Si 1 ( xi 1 ) Si ( xi 1 ), i 2, n
xi
ai S i ( xi ), i 1, n
bi S i ( xi ), i 1, n
ci S i ( xi ), i 1, n
d i S i ( xi ), i 1, n
Si 1 ( xi 1 ) bi 1
x xi 1 :
di
S i ( xi 1 ) bi ci ( xi 1 xi ) ( xi 1 xi ) 2
2
di 2
ci hi hi bi bi 1 , i 2, n
2
hi xi xi 1
19

26.

S i
S i 1
xi-2
xi-1
Si 1 ( xi 1 ) Si ( xi 1 ), i 2, n
xi
ai S i ( xi ), i 1, n
bi S i ( xi ), i 1, n
ci S i ( xi ), i 1, n
d i S i ( xi ), i 1, n
Si 1 ( xi 1 ) ci 1
x xi 1 :
S i ( xi 1 ) ci d i ( xi 1 xi )
hi xi xi 1
di hi ci ci 1 , i 2, n
20

27.

f (a) f (b) 0
S (a) S (b) 0
S1 ( x0 ) S n ( xn ) 0
x x0 : S1 ( x0 ) c1 d1 ( x0 x1 ) c1 d1h1 0
ai S i ( xi ), i 1, n
d i hi ci ci 1
bi S i ( xi ), i 1, n
i 1, если c0 0
ci S i ( xi ), i 1, n
d i S i ( xi ), i 1, n
S n ( xn ) сn 0

28.

Система уравнений для определения коэффициентов
кубического сплайна:
ai f ( xi ), i 0, n
21
ci 2 di 3
bi hi hi hi f ( xi ) f ( xi 1 ), i 1,n
2
6
di 2
ci hi hi bi bi 1 , i 2, n
2
di hi ci ci 1 , i 1, n; c0 cn 0
f ( xi 1 ) f ( xi ) f ( xi ) f ( xi 1 )
,
hi ci 1 2(hi hi 1 )ci hi 1ci 1 6
hi 1
hi
i 1, n 1; c0 cn 0
22

29.

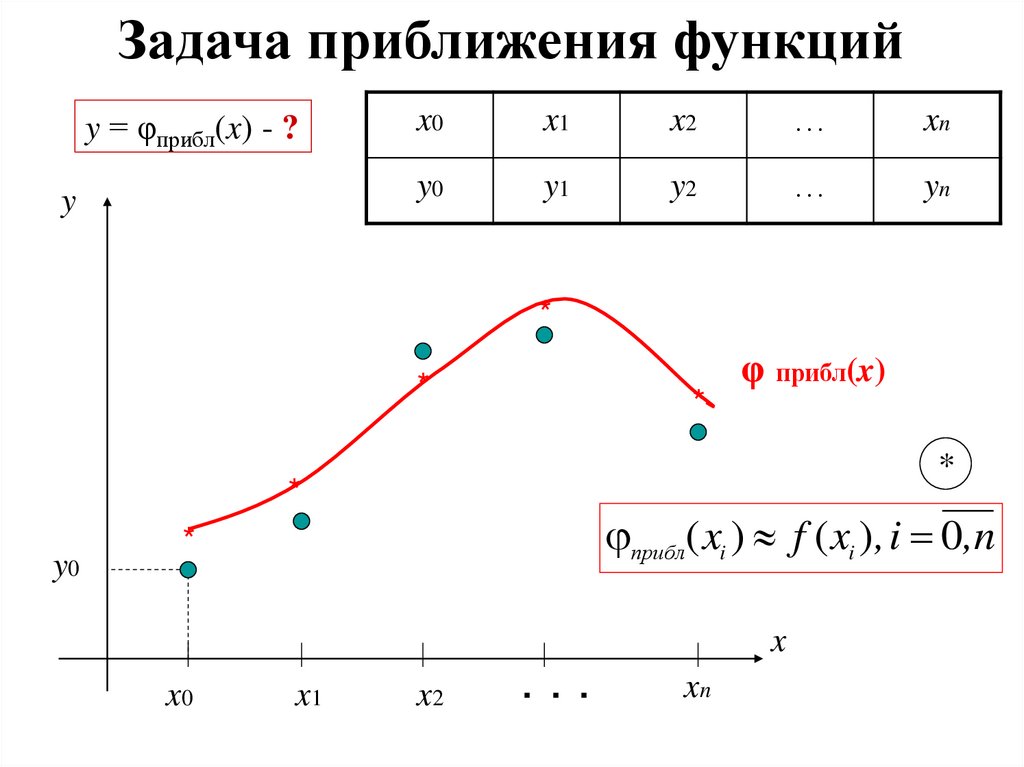
Задача приближения функций
y = φприбл(x) - ?
y
x0
x1
x2
…
xn
y0
y1
y2
…
yn
*
*
*
*
*
y0
φ прибл(x)
прибл ( xi ) f ( xi ), i 0,n
*
x
x0
x1
x2
. . .
xn

30. Метод подбора эмпирических формул

2 этапа решения:
- подбор общего вида формулы;
- определение наилучших значений коэффициентов формулы
1-й этап
y a0 a1 x
yi yi 1 yi
ki
, i 0, n 1
xi xi 1 xi
1
2
y a0 a1 x a2 x 2
2 yi yi 2 2 yi 1 yi , i 0, n 2

31.

2-й этап
y ( x, a0 , a1 , a2 , , am )
j m
( x, a0 , a1 , , am ) a j j ( x)
3
y a0 a1 x
j 0
y a0 a1 x a2 x 2
j m
i a j j ( x) yi min,
i 0, n
j 1
4

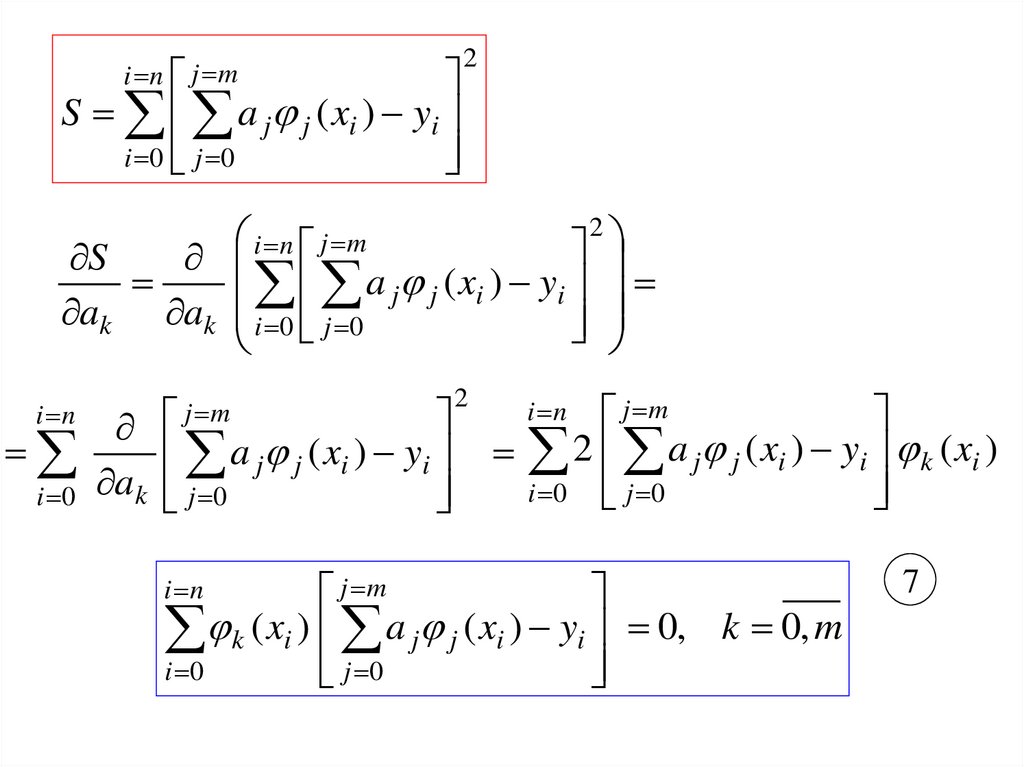
32. Метод наименьших квадратов

2
j m
2
S i a j j ( xi ) yi min
i 0
i 0 j 0
i n
i n
S
0;
a0
S
0;
a1
S
0
a m
6
5

33.

i n j m
S a j j ( xi ) yi
i 0
j 0
2
2
i n j m
S
a j j ( xi ) yi
ak ak i 0 j 0
a j j ( xi ) yi
i 0 ak
j 0
i n
j m
2
j m
2 a j j ( xi ) yi k ( xi )
i 0
j 0
i n
j m
k ( xi ) a j j ( xi ) yi 0, k 0, m
j 0
i 0
i n
7

34.

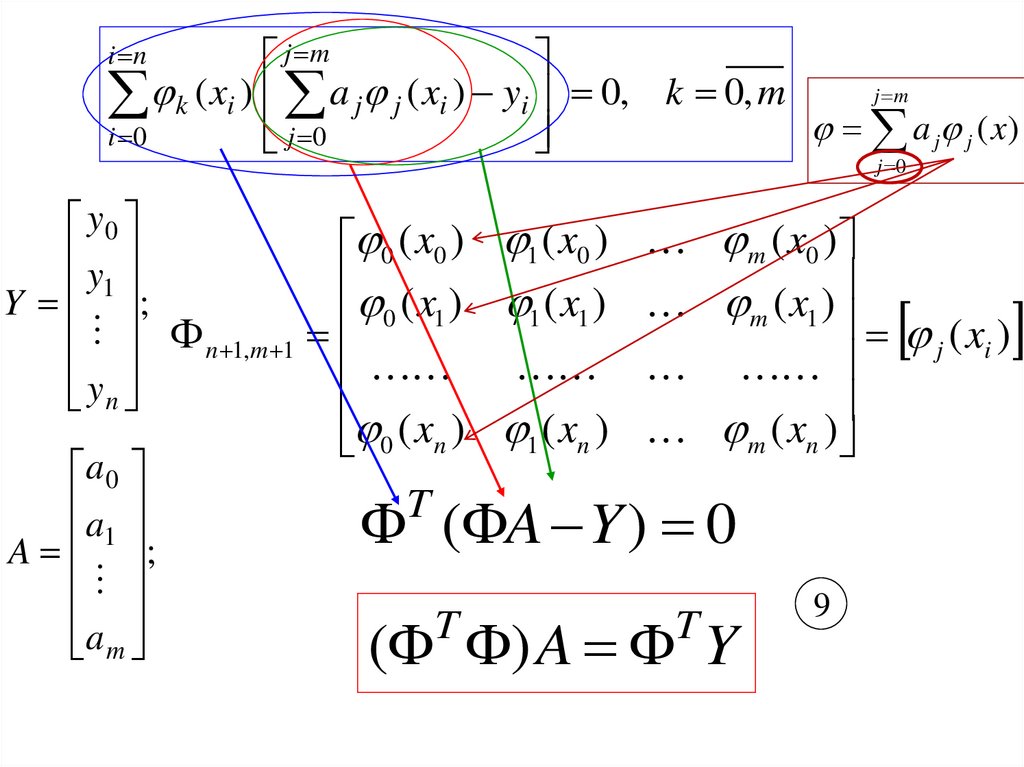
j m
k ( xi ) a j j ( xi ) yi 0, k 0, m j m a ( x)
j 0
i 0
j j
i n
j 0
y0
0 ( x0 ) 1 ( x0 ) m ( x0 )
y
( x ) ( x ) ( x )
Y 1 ;
1 1
m
1
n 1,m 1 0 1
j ( xi )
yn
a0
a
1
A
;
a m
0 ( xn ) 1 ( xn ) m ( xn )
T
( A Y ) 0
( ) A Y
T
T
9