04-Work-Energy

1. Работа. Энергия

ВоГУ
Лекция 04
Работа. Энергия
Кузина Л.А.,
к.ф.-м.н., доцент
2019 г.
1

2. План

1. Работа
2. Мощность
3. Энергия. Закон сохранения энергии
4. Кинетическая энергия
5. Потенциальная энергия в поле тяготения
6. Потенциальная энергия упругой деформации
7. Графическое представление энергии
8. Признак потенциальности поля.
Консервативные силы. Диссипативные
силы
9. Связь между консервативной силой и
потенциальной энергией
2

3.

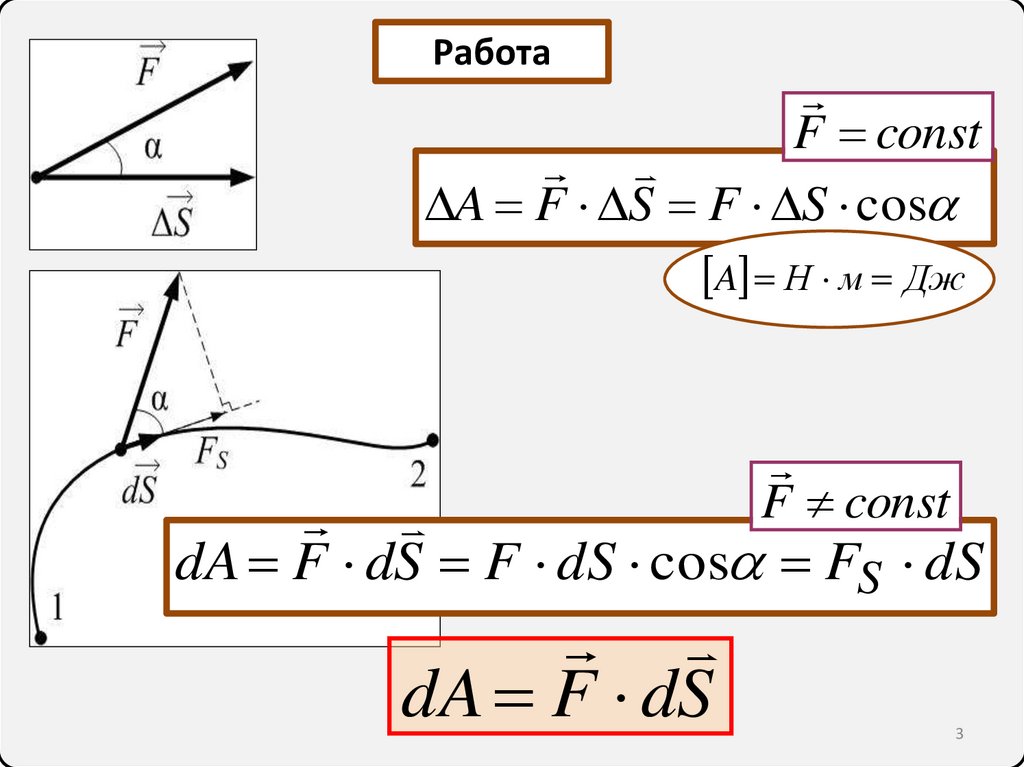
Работа
F const
A F S F S cos
A Н м Дж
F const
dA F dS F dS cos FS dS
dA F dS
3

4.

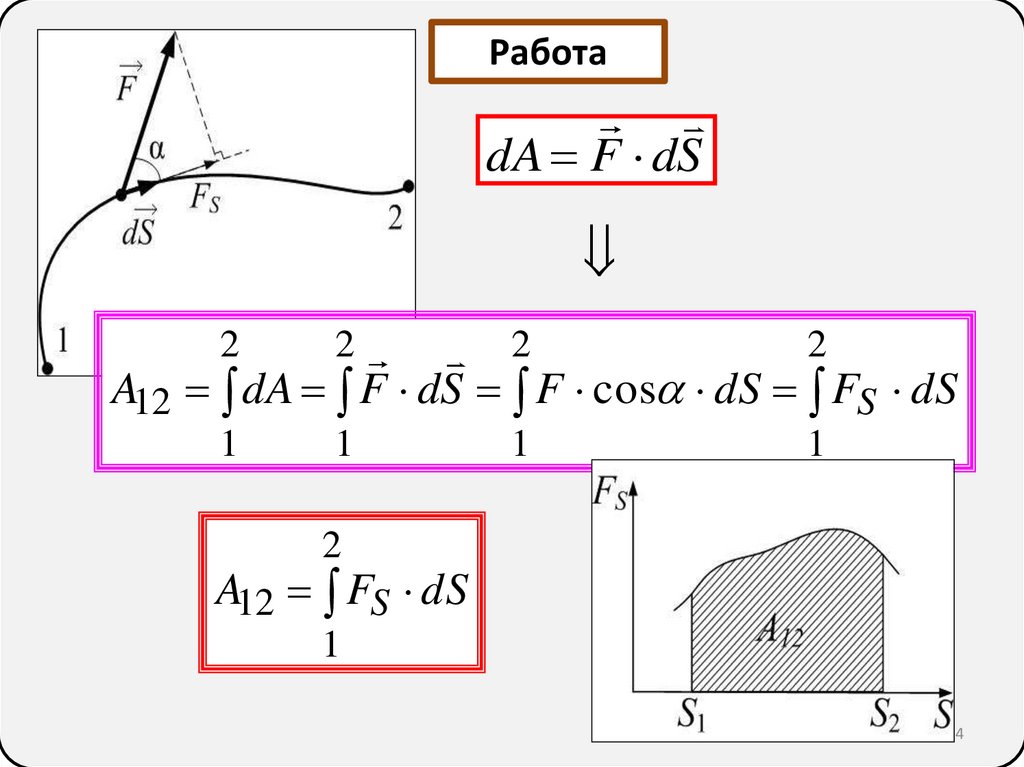
Работа
dA F dS
2
2
1
1
2
2
A12 dA F dS F cos dS FS dS
1
1
2
A12 FS dS
1
4

5.

Мощность – быстрота совершения работы
A
Средняя мощность Pср.
t
P Дж Вт
с
Мгновенная мощность
dA P dt
2
t2
1
t1
dA
P
dt
A12 dA P dt
dA F dS dS
P
F
F v
dt
dt
dt
5

6.

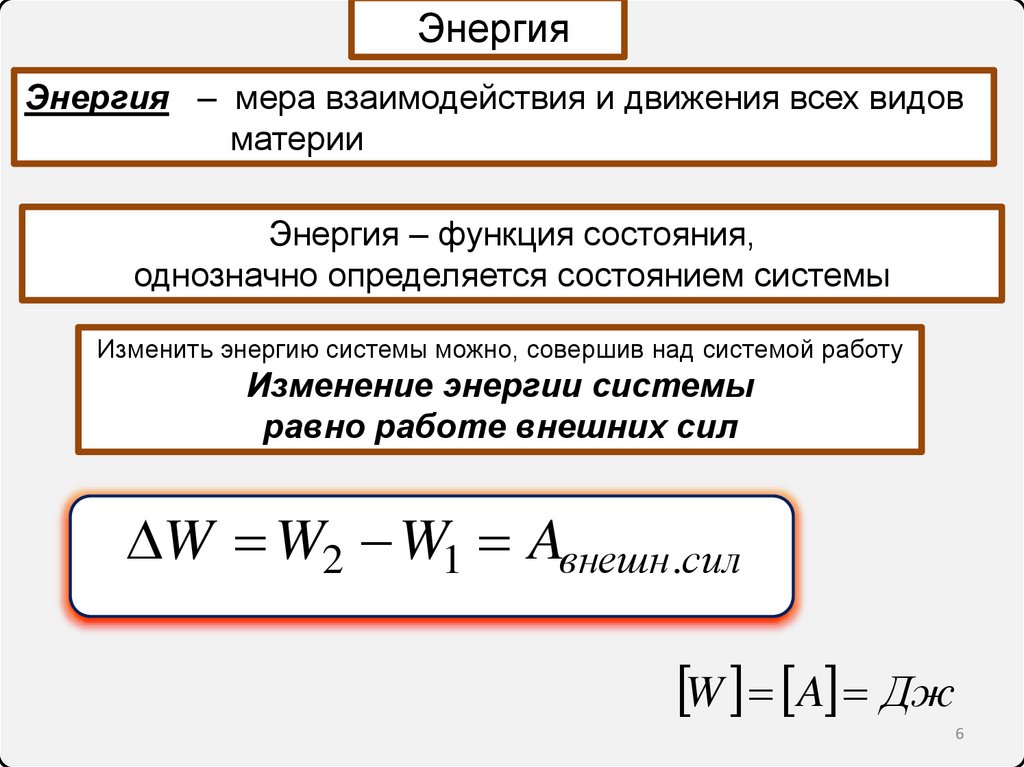
Энергия
Энергия – мера взаимодействия и движения всех видов
материи
Энергия – функция состояния,
однозначно определяется состоянием системы
Изменить энергию системы можно, совершив над системой работу
Изменение энергии системы
равно работе внешних сил
W W2 W1 Aвнешн.сил
W A Дж
6

7.

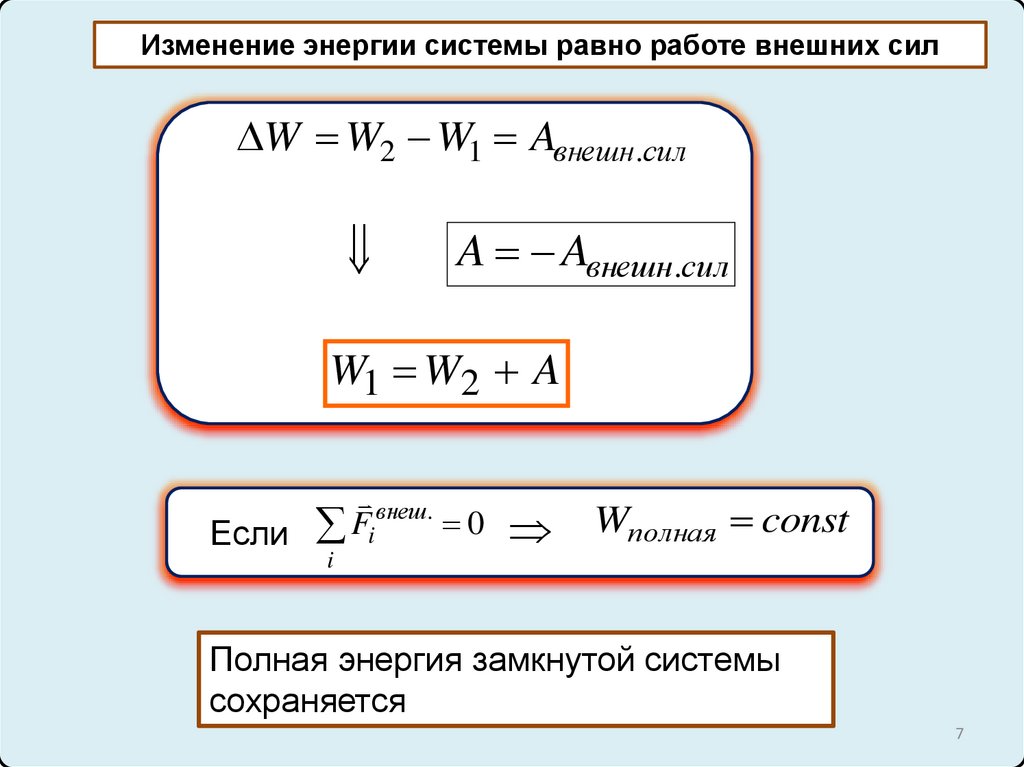
Изменение энергии системы равно работе внешних сил
W W2 W1 Aвнешн.сил
A Aвнешн.сил
W1 W2 A
внеш.
0
Если Fi
Wполная const
i
Полная энергия замкнутой системы
сохраняется
7

8.

Механическая энергия
Кинетическая
(энергия
движения)
Потенциальная
(энергия взаимодействия;
положения, поскольку
величина взаимодействия
зависит от положения тел)
8

9.

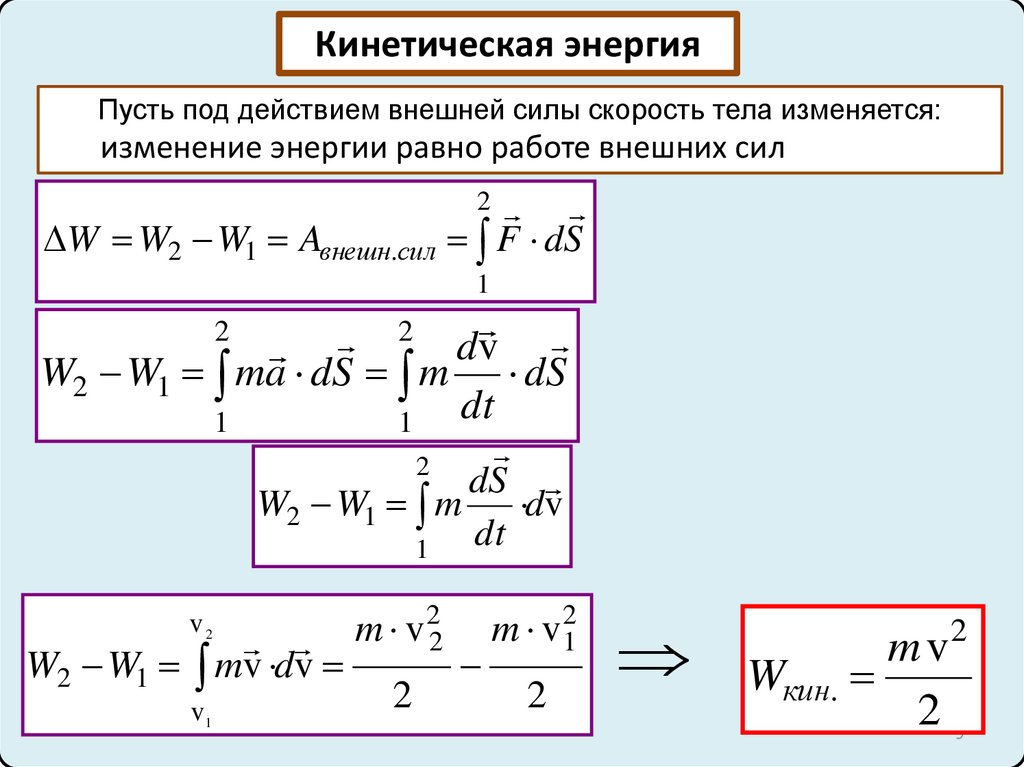
Кинетическая энергия
Пусть под действием внешней силы скорость тела изменяется:
изменение энергии равно работе внешних сил
W W2 W1 Aвнешн.сил F dS
2
1
2
dv
W2 W1 ma dS m dS
dt
1
1
2
dS
W2 W1 m
dv
dt
1
2
v2
W2 W1 mv dv
v1
m v 22
2
m v 21
2
mv
Wкин.
2
2
9

10.

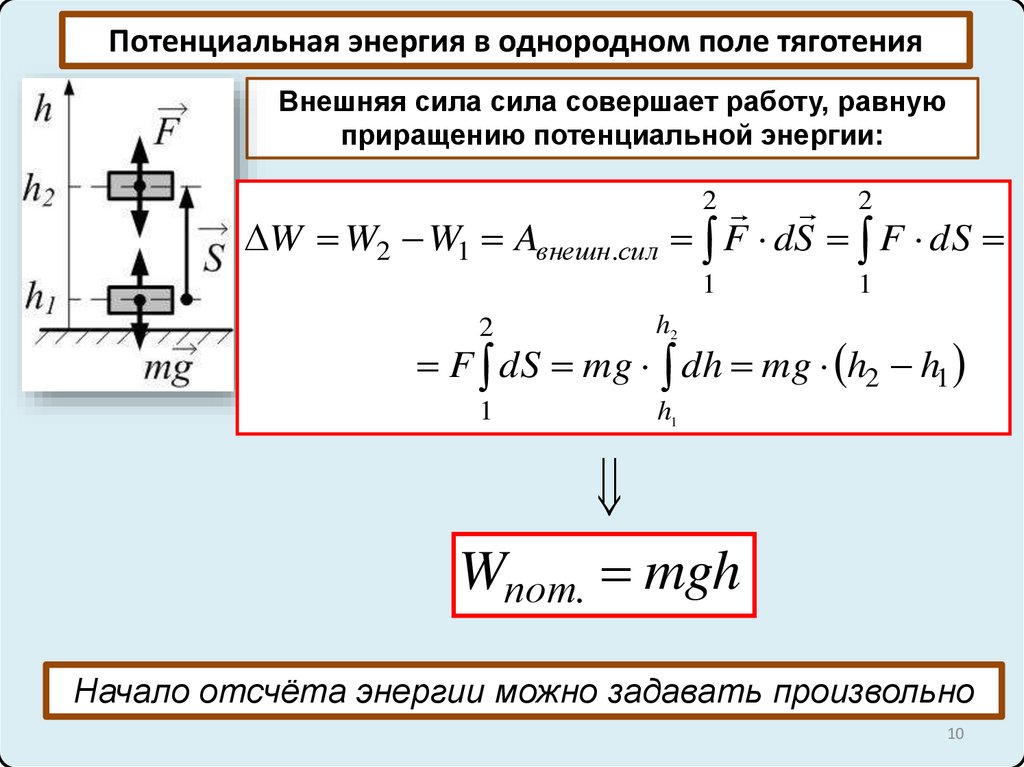
Потенциальная энергия в однородном поле тяготения
Внешняя сила сила совершает работу, равную
приращению потенциальной энергии:
2
W W2 W1 Aвнешн.сил F dS F dS
2
1
2
h2
1
h1
1
F dS mg dh mg h2 h1
Wпот. mgh
Начало отсчёта энергии можно задавать произвольно
10

11.

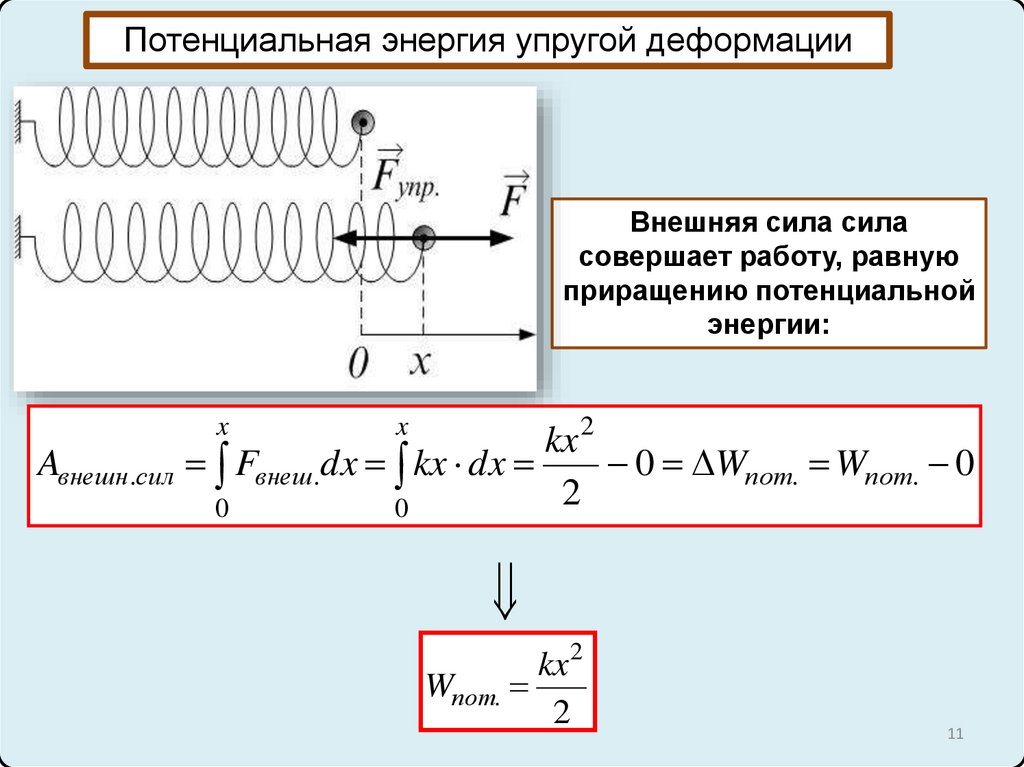
Потенциальная энергия упругой деформации
Внешняя сила сила
совершает работу, равную
приращению потенциальной
энергии:
kx 2
Aвнешн.сил Fвнеш.dx kx dx
0 Wпот. Wпот. 0
2
0
0
x
x
kx 2
Wпот.
2
11

12.

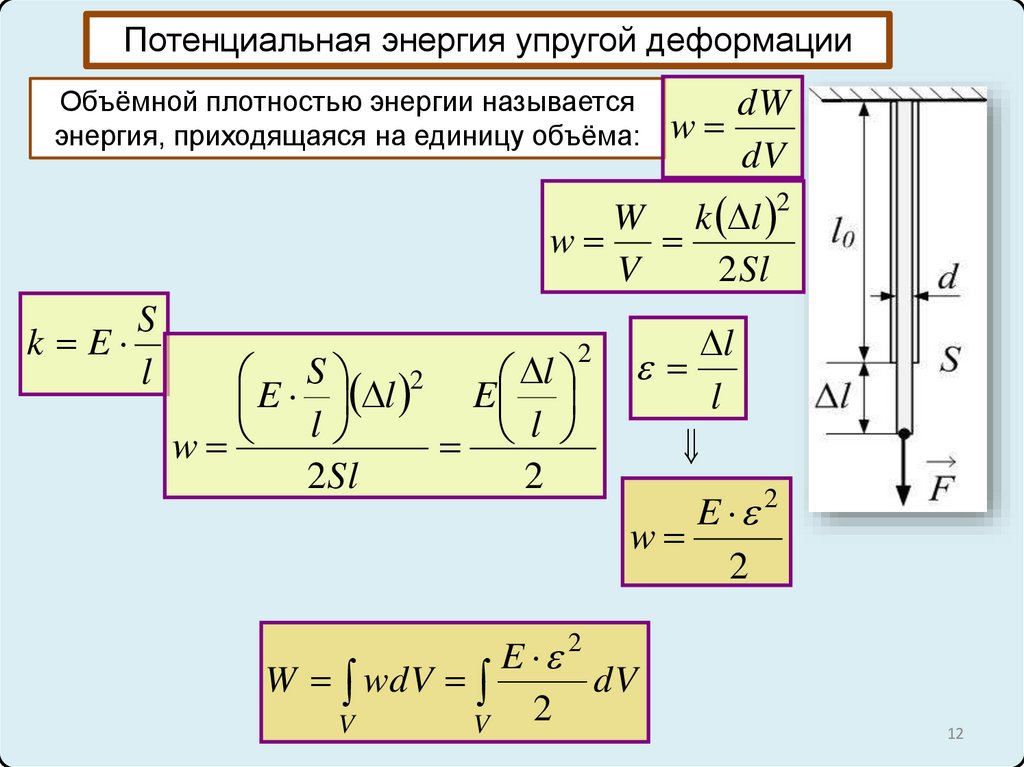
Потенциальная энергия упругой деформации
Объёмной плотностью энергии называется
энергия, приходящаяся на единицу объёма:
dW
w
dV
W k l 2
w
V
2 Sl
S
k E
l
S
l
2
E
E l
l
l
w
2Sl
2
2
l
l
E 2
w
2
E 2
W wdV
dV
2
V
V
12

13.

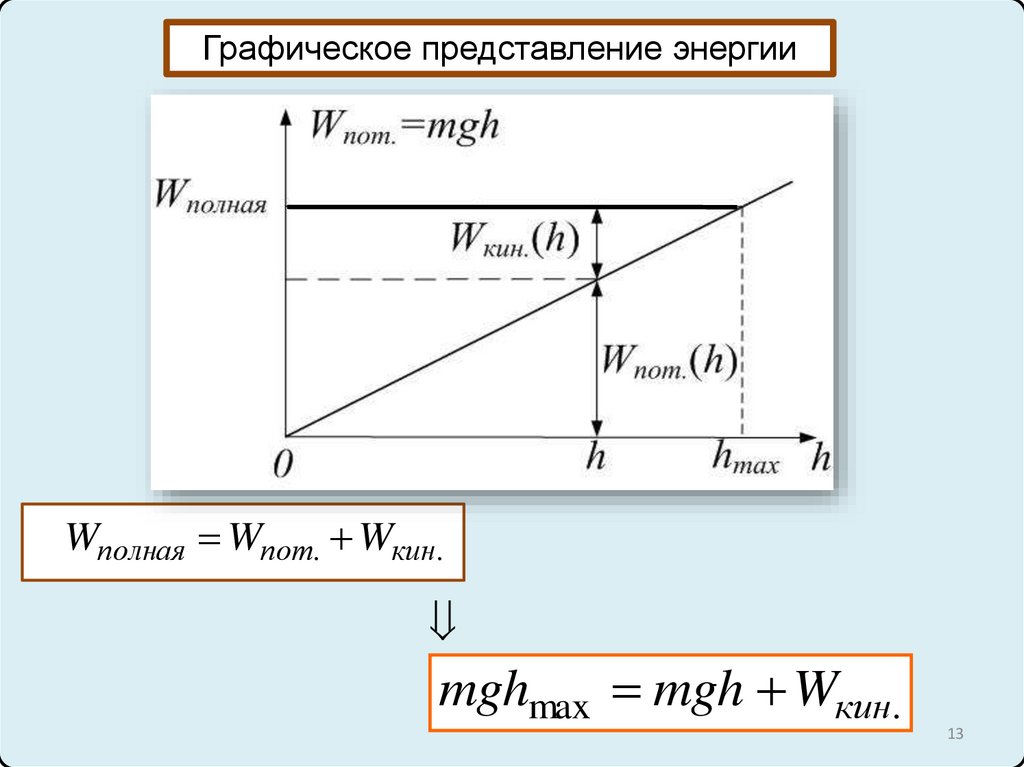
Графическое представление энергии
Wполная Wпот. Wкин.
mghmax mgh Wкин.
13

14.

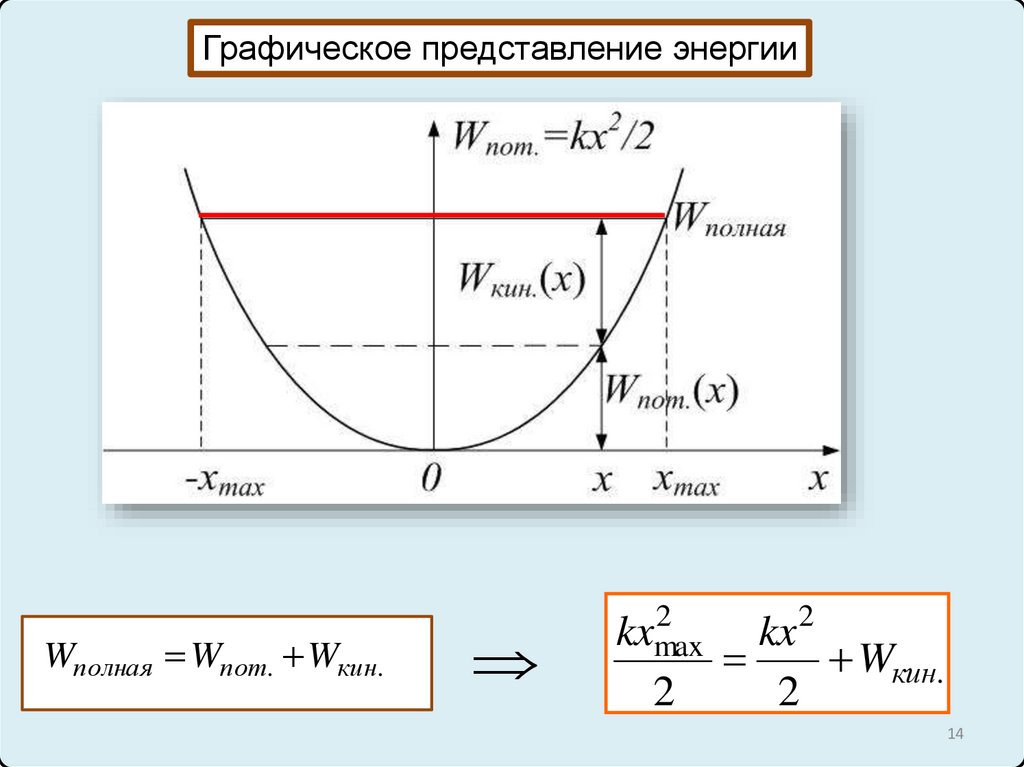
Графическое представление энергии
Wполная Wпот. Wкин.
2
kxmax
2
2
kx
Wкин.
2
14

15.

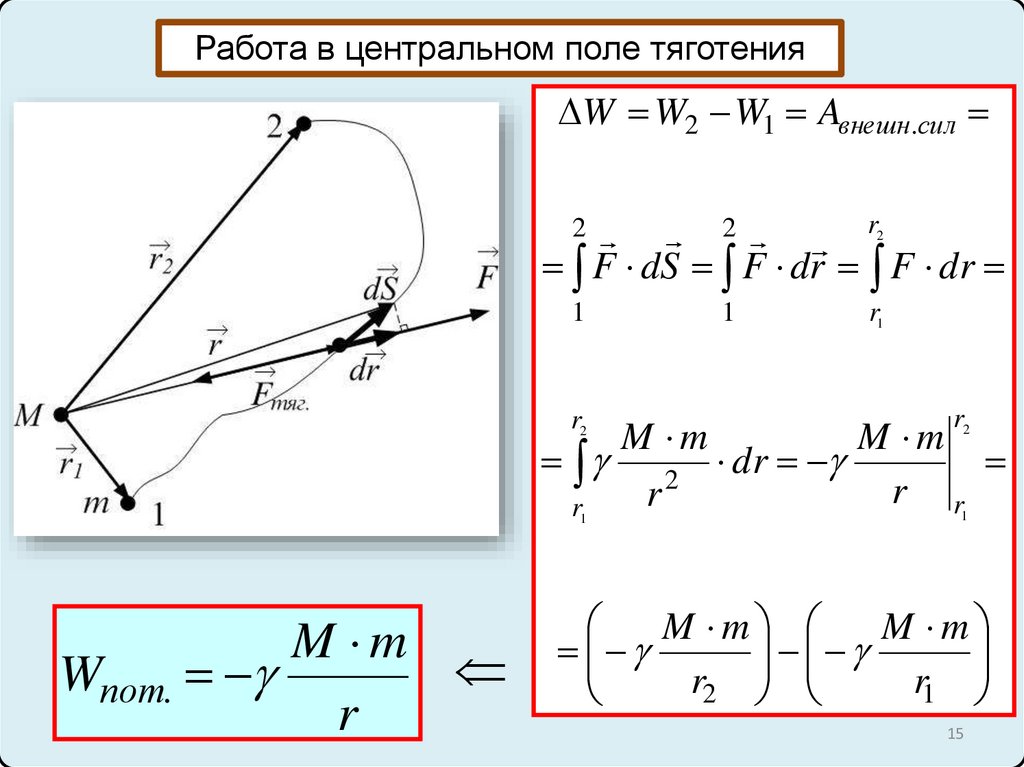
Работа в центральном поле тяготения
W W2 W1 Aвнешн.сил
2 r
F dS F dr F dr
2
1
2
1
r1
r2
r2
1
1
M m
M m
2 dr
r r
r
r
M m
Wпот.
r
M m
M m
r2
r1
15

16.

Работа в центральном поле тяготения
M m
M m
W W2 W1 Aвнешн.сил Aграв.сил
r2
r1
Выводы:
1. Потенциальная энергия взаимодействия точечных масс
M m (при r W 0 )
Wпот.
r
2. Работа сил гравитационного поля не зависит от
траектории, а только от начального и конечного положения
точки. Такие поля называются потенциальными
3. Потенциал гравитационного поля:
Wпот.
m
Дж
кг
16

17.

Признак потенциальности поля
Консервативные силы
Диссипативные силы
Сила называется консервативной, если её работа не зависит от
траектории, а только от начального и конечного положения
тела
Поле таких сил называется потенциальным
Примеры: гравитационное поле; поле упругих сил
Если работа силы зависит от траектории, то силы называются
диссипативными
Поле таких сил – непотенциальное
Примеры: силы трения; силы вязкости; силы неупругой
деформации
При наличии диссипативных сил механическая энергия необратимо
превращается в другие виды, например, в тепловую
17

18.

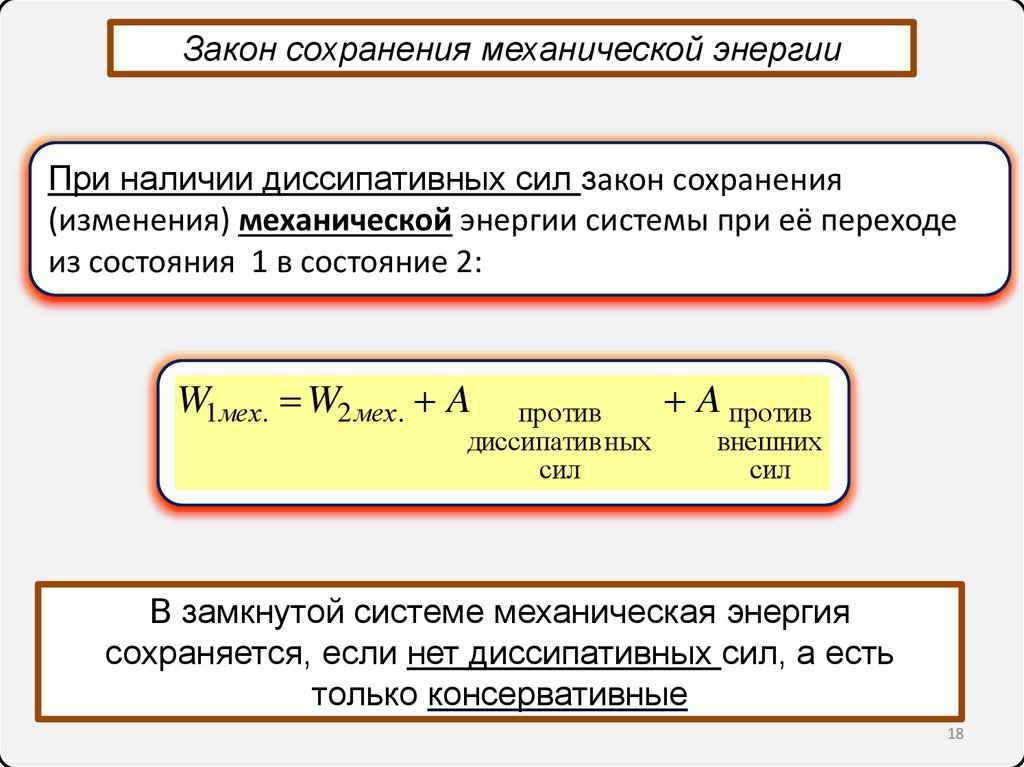
Закон сохранения механической энергии
При наличии диссипативных сил закон сохранения
(изменения) механической энергии системы при её переходе
из состояния 1 в состояние 2:
W1мех. W2 мех. A
A против
против
диссипатив ных
внешних
сил
сил
В замкнутой системе механическая энергия
сохраняется, если нет диссипативных сил, а есть
только консервативные
18

19.

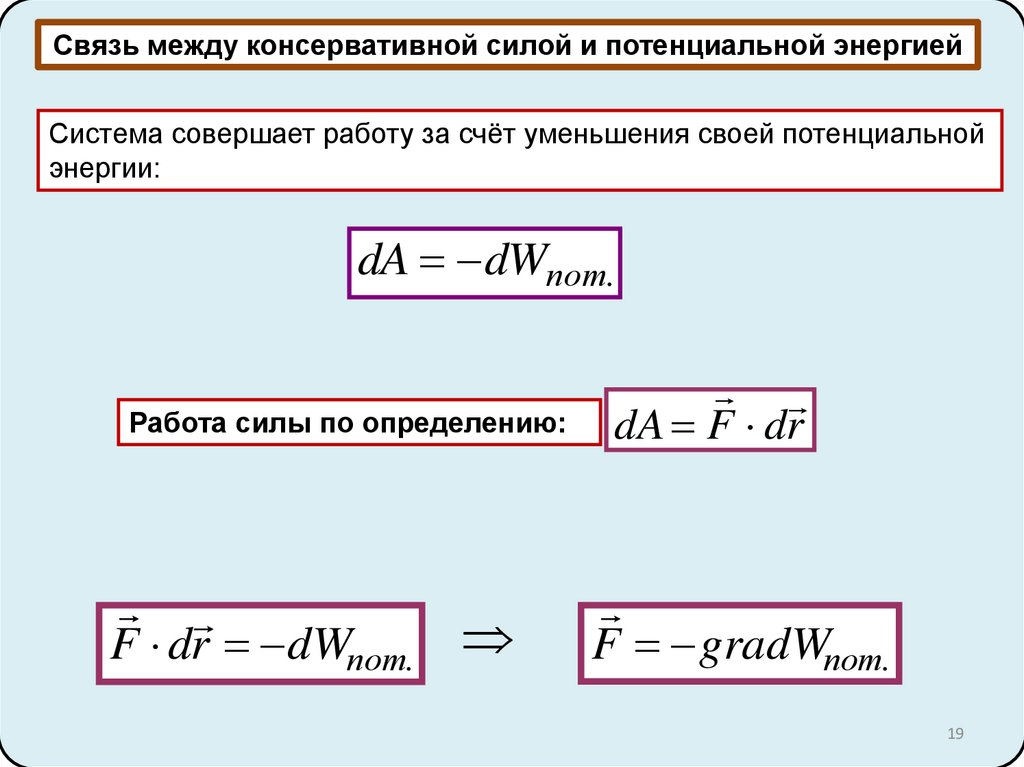
Связь между консервативной силой и потенциальной энергией
Система совершает работу за счёт уменьшения своей потенциальной
энергии:
dA dWпот.
Работа силы по определению:
F dr dWпот.
dA F dr
F gradWпот.
19

20.

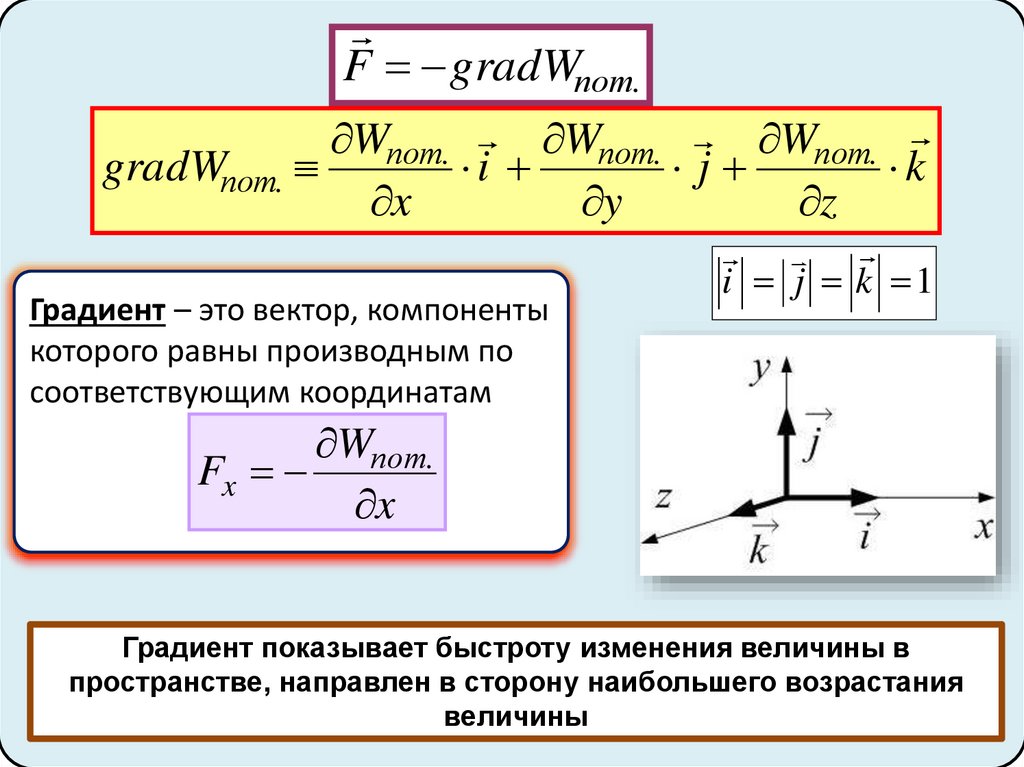
F gradWпот.
Wпот. Wпот. Wпот.
gradWпот.
i
j
k
x
y
z
Градиент – это вектор, компоненты
которого равны производным по
соответствующим координатам
i j k 1
Wпот.
Fx
x
Градиент показывает быстроту изменения величины в
пространстве, направлен в сторону наибольшего возрастания
величины
20

21.

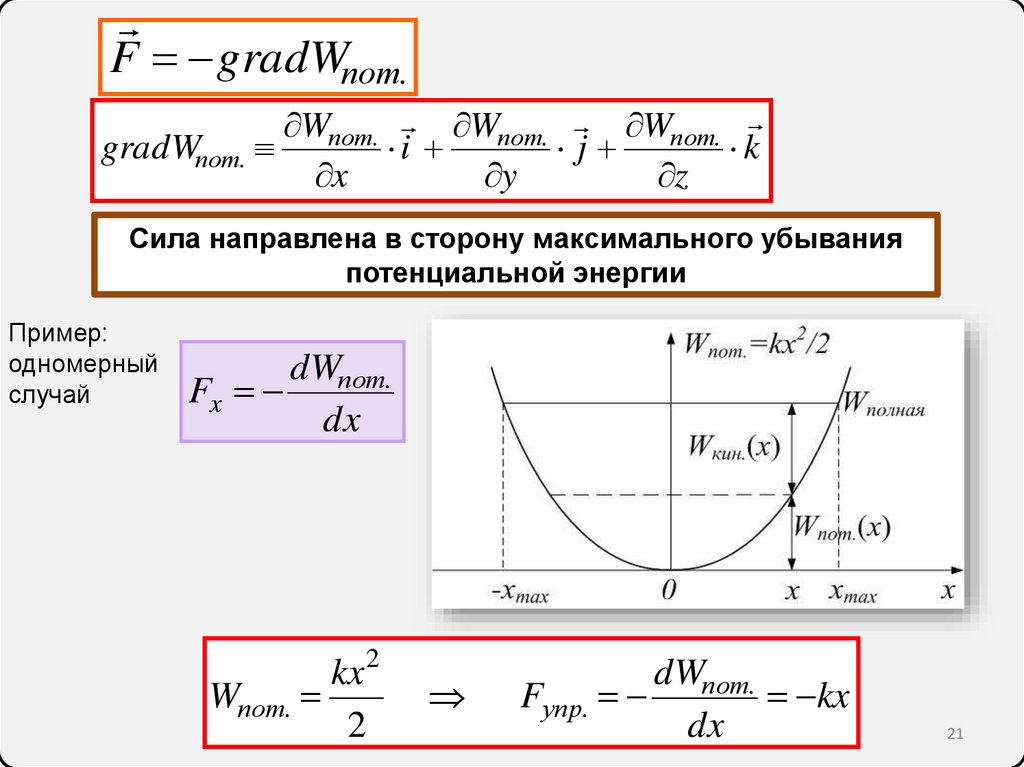
F gradWпот.
Wпот. Wпот. Wпот.
gradWпот.
i
j
k
x
y
z
Сила направлена в сторону максимального убывания
потенциальной энергии
Пример:
одномерный
случай
dWпот.
Fx
dx
kx 2
Wпот.
2
dWпот.
Fупр.
kx
dx
21

22.

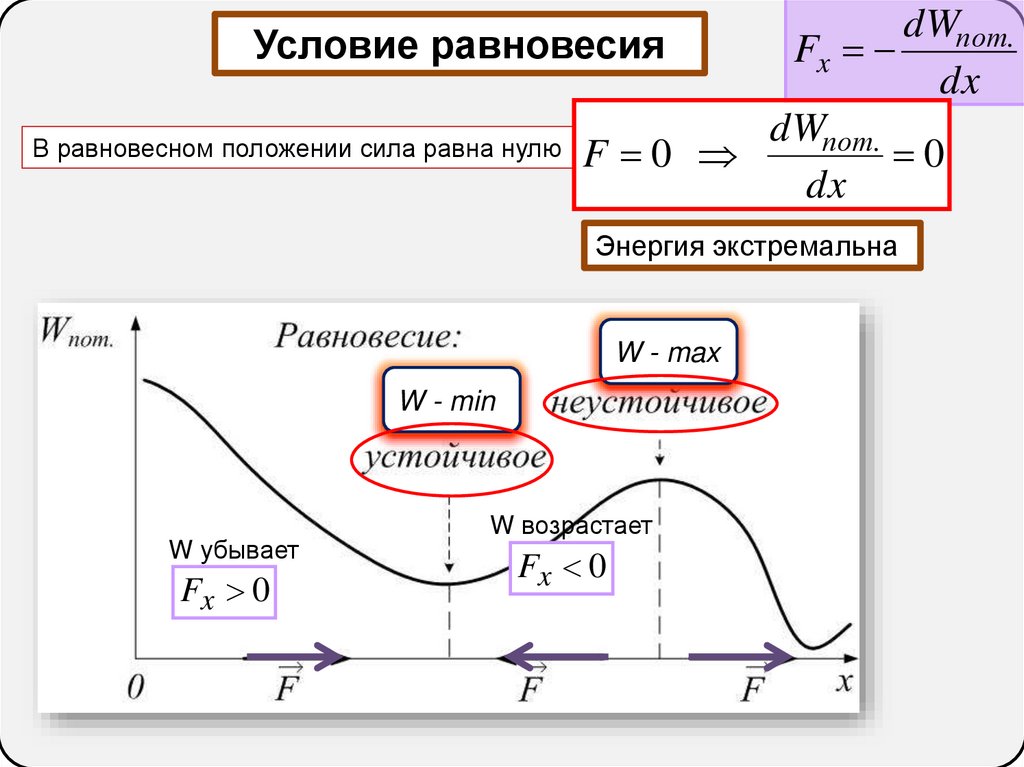
dWпот.
Условие равновесия
Fx
dx
dWпот.
В равновесном положении сила равна нулю F 0
0
dx
Энергия экстремальна
W - max
W - min
W убывает
Fx 0
W возрастает
Fx 0