Похожие презентации:
Слайд-лекция_№3,4__Теория_пределов._Замечательные_пределы
1. Предел функции в точке
ПРЕДЕЛ ФУНКЦИИ В ТОЧКЕПусть функция y = f(x) определена в некоторой окрестности точки
x0, кроме, быть может самой точки x0.
Число А называют пределом функции в точке x0 (или при x x0),
если для любого положительного ε найдется такое положительное
число δ, что для всех х из δ – окрестности точки x0 справедливо
неравенство:
f (x) A
0; 0; x : x x0 f ( x ) A
lim f ( x ) A
x x0
2. Предел функции в точке
ПРЕДЕЛ ФУНКЦИИ В ТОЧКЕ0; 0; x : x x0 f ( x ) A
ε окрестность точки А
y
2
А
0
х0
х
δ окрестность точки x0
Геометрический смысл предела: для всех х из δ – окрестности точки
x0 точки графика функции лежат внутри полосы, шириной 2ε,
ограниченной прямыми: у = А + ε , у = А - ε .
3. Односторонние пределы
ОДНОСТОРОННИЕ ПРЕДЕЛЫВ определении предела функции
lim f ( x ) A
x x0
предполагается, что x стремится к x0 любым способом: оставаясь
меньше, чем x0 (слева от x0), большим, чем x0 (справа от x0), или
колеблясь около точки x0.
Бывают случаи, когда способ приближения аргумента x к x0
существенно влияет на значение предела, поэтому вводят понятия
односторонних пределов.
Число А1 называют пределом функции слева в точке x0, если для
любого ε > 0 найдется такое δ >0, что для всех
x ( x0 ; x0 )
справедливо неравенство:
f ( x ) A1
Предел слева записывают так:
lim
f
(
x
)
A
1
x x 0
0
4. Односторонние пределы
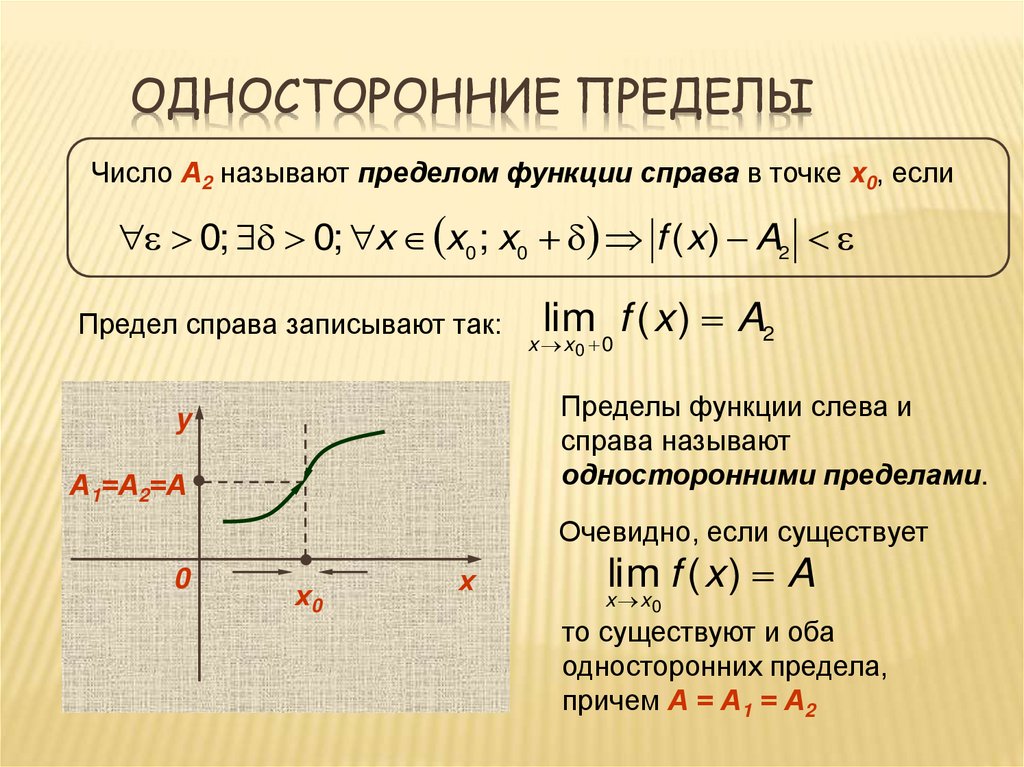
ОДНОСТОРОННИЕ ПРЕДЕЛЫЧисло А2 называют пределом функции справа в точке x0, если
0; 0; x x0 ; x0 f ( x ) A2
Предел справа записывают так:
Пределы функции слева и
справа называют
односторонними пределами.
y
А2
А1=А2=А
А1
0
lim f ( x ) A2
x x0 0
Очевидно, если существует
х0
х
lim f ( x ) A
x x0
то существуют и оба
односторонних предела,
причем А = А1 = А2
5. Предел функции при x стремящемся к бесконечности
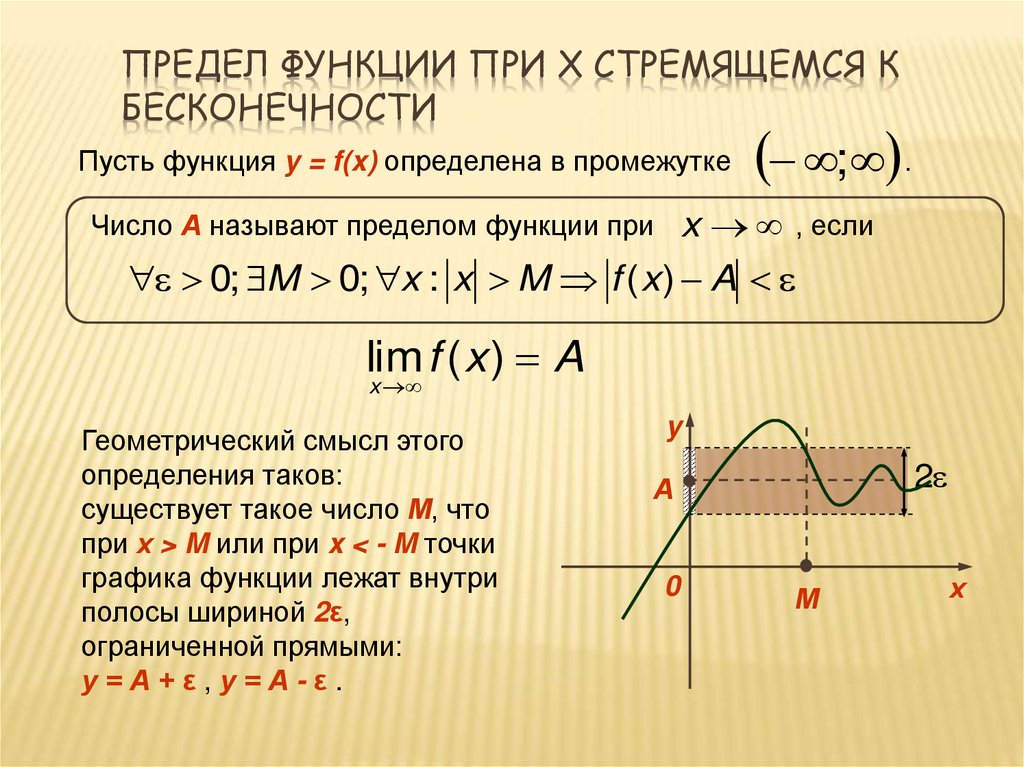
ПРЕДЕЛ ФУНКЦИИ ПРИ X СТРЕМЯЩЕМСЯ КБЕСКОНЕЧНОСТИ
Пусть функция y = f(x) определена в промежутке
; .
x , если
Число А называют пределом функции при
0; M 0; x : x M f ( x ) A
lim f ( x ) A
x
Геометрический смысл этого
определения таков:
существует такое число М, что
при х > M или при x < - M точки
графика функции лежат внутри
полосы шириной 2ε,
ограниченной прямыми:
у=А+ε,у=А-ε.
y
2
А
0
М
х
6.
Функция f(x) называется бесконечно большойвеличиной, если для любого, даже сколь угодно
большого числа
0
M 0
, что для всех
найдется такое число
и удовлетворяющих условию
x x0
x x0
выполняется неравенство
f ( x) M
7.
Если f ( x) M тоlim
f
(
x
)
x x
0
Если f ( x) M
то
lim
f
(
x
)
x x
0
8.
Функцияy tgx
является бесконечно большой величиной
при
x
поскольку
2
lim tgx
x
2
9.
Бесконечно большая величинаявляется неограниченной
функцией при
x x0 или при x
но в то же время
неограниченная функция не
обязательно бесконечно
большая.
10.
Функцияy x sin x
является неограниченной функцией, но
при
x
она не будет бесконечно большой,
поскольку ее значения колеблются,
переходя
от
положительных
к
отрицательным через ноль.
11.
1Сумма бесконечно большой величины
и ограниченной функции есть величина
бесконечно большая.
12.
2Произведение бесконечно большой
величины на функцию, предел которой
отличен от нуля, есть величина
бесконечно большая.
3
Частное от деления бесконечно большой
величины на функцию, имеющую предел,
есть величина бесконечно большая.
13.
f ( x) tgxФункция
является бесконечно большой при x
( x) 4 x 3
имеет предел при x
2
Функция
lim ( 4 x 3) 2 3 0
x
2
2
14.
Функция( x) sin x
является ограниченной.
Тогда функции
f ( x) ( x) tgx sin x
f ( x)
tgx
( x) 4 x 3
являются
бесконечно
величинами при
x
2
большими
15.
Функция f(x) называется бесконечномалой величиной, если при
x x0 или при x
ее предел равен нулю:
lim f ( x) 0
x x0
или
lim f ( x) 0
x
16.
Функцияy cos x
является бесконечно малой величиной
при
x
поскольку
2
lim cos x 0
x
2
17.
Если функция f(x) имеет приx x0 или при x
предел, равный А, то ее можно
представить в виде суммы
этого числа А и бесконечно
малой величины
(x) при x x0 или x
lim f ( x) A
x x0
x
f ( x) A ( x)
18.
Верна и обратнаяЕсли функцию f(x) можно
представить как сумму числа А
и бесконечно малой величины
(x) при x x0 или x
то число А является пределом
этой функции при
x x0 или при x
f ( x) A ( x) lim
f
(
x
)
A
x x
0
x
19.
1Алгебраическая сумма бесконечно малых величин
есть величина бесконечно малая.
2
Произведение бесконечно малой величины на
ограниченную функцию есть величина бесконечно малая.
3
Частное от деления бесконечно малой величины
на функцию, предел которой отличен от нуля,
есть величина бесконечно малая.
20.
Пусть( x) 5x 10 ( x) lg( x 1)
являются
бесконечно
величинами при x 2
малыми
поскольку
lim (5x 10) 0
x 2
lim lg( x 1) 0
x 2
Функция
f ( x) sin x
21.
является ограниченнойпромежутке, поскольку
на
любом
sin x 1
( x) x 5
Функция
2
имеет предел при x 2
lim ( x 5) 1
2
x 2
Тогда функции
( x) ( x) 5x 10 lg( x 1)
22.
( x) f ( x) (5x 10) sin x( x) f ( x) lg( x 1) sin x
( x) ( x) (5x 10) lg( x 1)
( x) 5 x 10
2
( x) x 5
являются
бесконечно
величинами при x 2
малыми
23.
Предел отношениямалых величин
двух
( x)
lim
x x
( x)
x
бесконечно
0
может
быть равен нулю, тогда α(х)
называется бесконечно малой более
высокого порядка, чем β(х);
может быть равен числу А, не равному
нулю,
тогда
α(х)
и
β(х)
имеют
одинаковый порядок малости;
может
быть равен бесконечности,
тогда α(х) называется бесконечно малой
более низкого порядка, чем β(х).
24.
Связь между бесконечно малыми и бесконечно большимивеличинами выражается следующей теоремой:
Если функция α(х) -бесконечно
малая величина при
x x0 или при
x
1
то функция f ( x)
( x)
есть величина бесконечно
большая при
x x0 или при x
25.
Если функция α(х) -бесконечнобольшая величина при
x x0 или при
то функция
x
1
f ( x)
( x)
есть величина бесконечно малая
при
x x0 или при x
26.
y cos xФункция
является бесконечно малой величиной
при x
2
Тогда функция
1
y
cos x
является бесконечно большой величиной
при x
2
27. Основные теоремы о пределах
ОСНОВНЫЕ ТЕОРЕМЫ О ПРЕДЕЛАХРассмотрим теоремы, которые облегчают нахождение пределов
функций.
Формулировка теорем, когда x x0 или x аналогичны,
поэтому будем пользоваться обозначением: lim f ( x ).
Предел суммы (разности) двух функций равен сумме (разности)
пределов:
lim f1( x ) f2 ( x ) lim f1( x ) limf2 ( x )
Предел произведения двух функций равен произведению
пределов:
lim f1( x ) f2 ( x ) lim f1( x ) lim f2 ( x )
Постоянный множитель можно выносить за знак предела:
lim C f ( x ) C lim f ( x )
28. Основные теоремы о пределах
ОСНОВНЫЕ ТЕОРЕМЫ О ПРЕДЕЛАХПредел дроби равен пределу числителя, деленному на предел
знаменателя, если предел знаменателя не равен нулю:
f1( x ) lim f1( x )
lim
f2 ( x ) lim f2 ( x )
lim f ( x ) 0
2
Предел степени с натуральным показателем равен той же
степени предела:
lim f ( x ) lim f ( x )
n
n
Предел показательно – степенной функции:
lim f ( x )
g(x)
lim f ( x )
lim g ( x )
29. Основные теоремы о пределах
ОСНОВНЫЕ ТЕОРЕМЫ О ПРЕДЕЛАХЕсли между соответствующими значениями трех функций
u u( x );
z z( x ); v v ( x )
выполняются неравенства: u z v, при этом:
lim u( x ) lim v ( x ) A тогда: lim z( x ) A
Если функция f(x) монотонна и ограничена при x < x0 или при
x > x0, то существует соответственно ее левый предел:
lim
f
(
x
)
A
1
x x 0
0
или ее правый предел:
lim f ( x ) A2
x x0 0
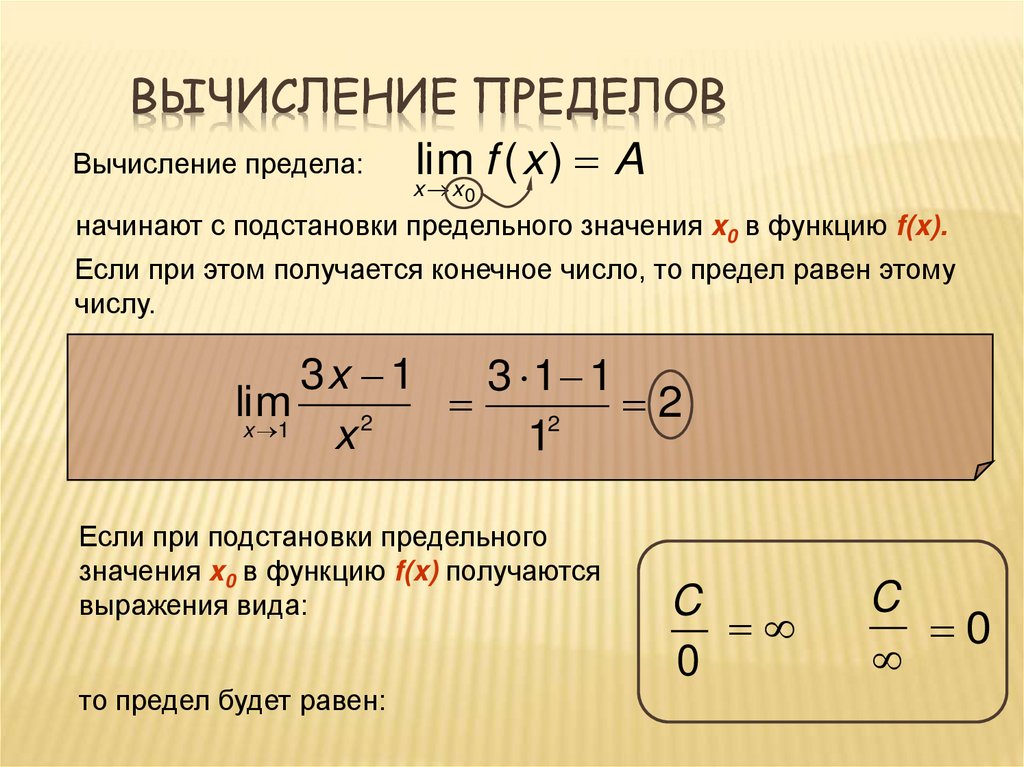
30. Вычисление пределов
ВЫЧИСЛЕНИЕ ПРЕДЕЛОВВычисление предела:
lim f ( x ) A
x x
0
начинают с подстановки предельного значения x0 в функцию f(x).
Если при этом получается конечное число, то предел равен этому
числу.
3x 1
3 1 1
lim
2
2
2
x 1
x
1
Если при подстановки предельного
значения x0 в функцию f(x) получаются
выражения вида:
то предел будет равен:
C
0
C
0
31. Вычисление пределов
ВЫЧИСЛЕНИЕ ПРЕДЕЛОВЧасто при подстановке предельного значения x0 в функцию f(x)
получаются выражения следующих видов:
0
;
0
; 0 ; 1 ; 0 0 ; 0 ; 0 ;
Эти выражения называются неопределенности, а вычисление
пределов в этом случае называется раскрытие
неопределенности.
32. Раскрытие неопределенностей
РАСКРЫТИЕ НЕОПРЕДЕЛЕННОСТЕЙРаскрытие неопределенности
0
0
x 2 14 x 32
0
x 2 x 16
lim
lim
2
x 2
x 2
x 6x 8
0
x 2 x 4
x 16 18
lim
9
x 2
x 4
2
Если f(x) – дробно –
рациональная
x 1 1 x 1 1
0
x 1 1 функция,
необходимо разложить
наlim
lim
Если f(x) – иррациональная
x
0
x 0
0
x
множители
числитель
и
x 1 умножить
1
дробь, x
необходимо
знаменатель дроби
числитель и знаменатель
x 1 1
1дроби на выражение,
1
lim
lim
числителю.
x 0
x 0
сопряженное
x x 1 1
x 1 1 2
33. Раскрытие неопределенностей
РАСКРЫТИЕ НЕОПРЕДЕЛЕННОСТЕЙРаскрытие неопределенности
2
2x
3x 1
2 2
2
2x 2 3 x 1
x
x
x
lim
lim
x
x 4 x 2
4 x 2 2x 5
2x 5
2 2
2
x
x
x
3 1
2 2
C
2 0 0 1
x
x
lim
f(x) – дробно
0 –
Если
x
2 5рациональная
4 0 0 2
функция
или
4 2
x x иррациональная дробь
необходимо разделить
числитель и знаменатель
дроби на x в старшей степени
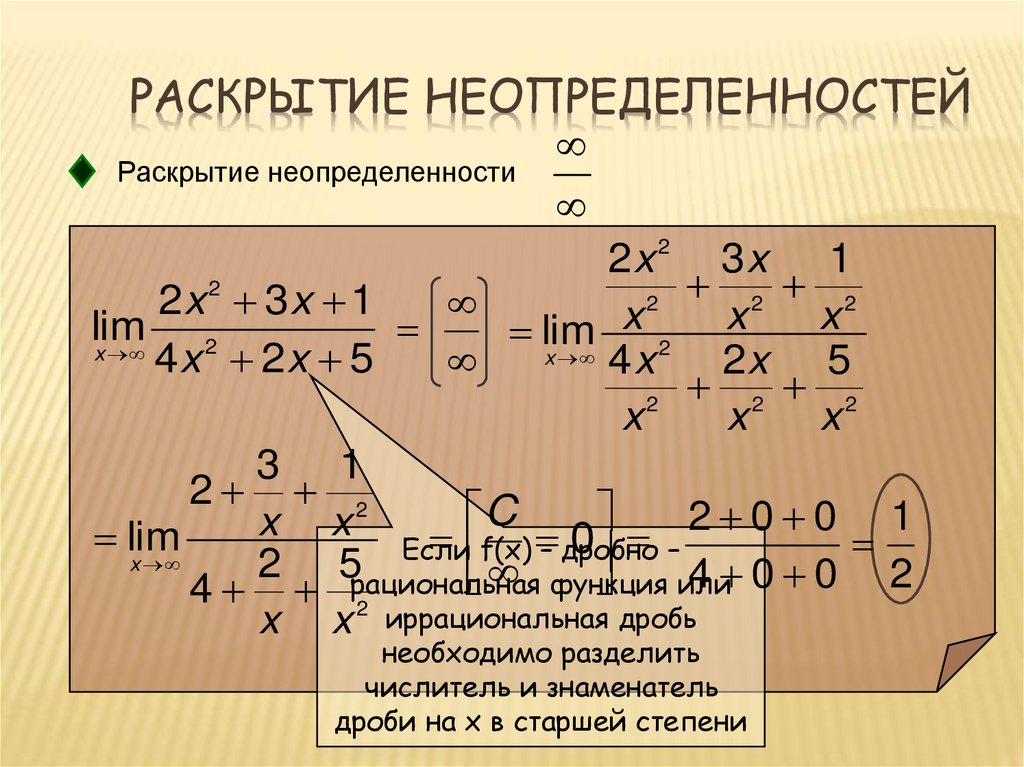
34. Раскрытие неопределенностей
РАСКРЫТИЕ НЕОПРЕДЕЛЕННОСТЕЙРаскрытие неопределенности
2
2
lim
x
1
x
1
x
x 1 x 1 x 1 x 1
lim
x 1 x 1
2
x
lim
x
2
2
2
2
2
Умножим и разделим
2
( x 1) ( x функцию
1)
на
сопряженное
lim
2
x
2
2
выражение.
2
2
x 1 x 1
2
0
x 1 x 1
2
35.
sin xlim
1
x 0
x
36.
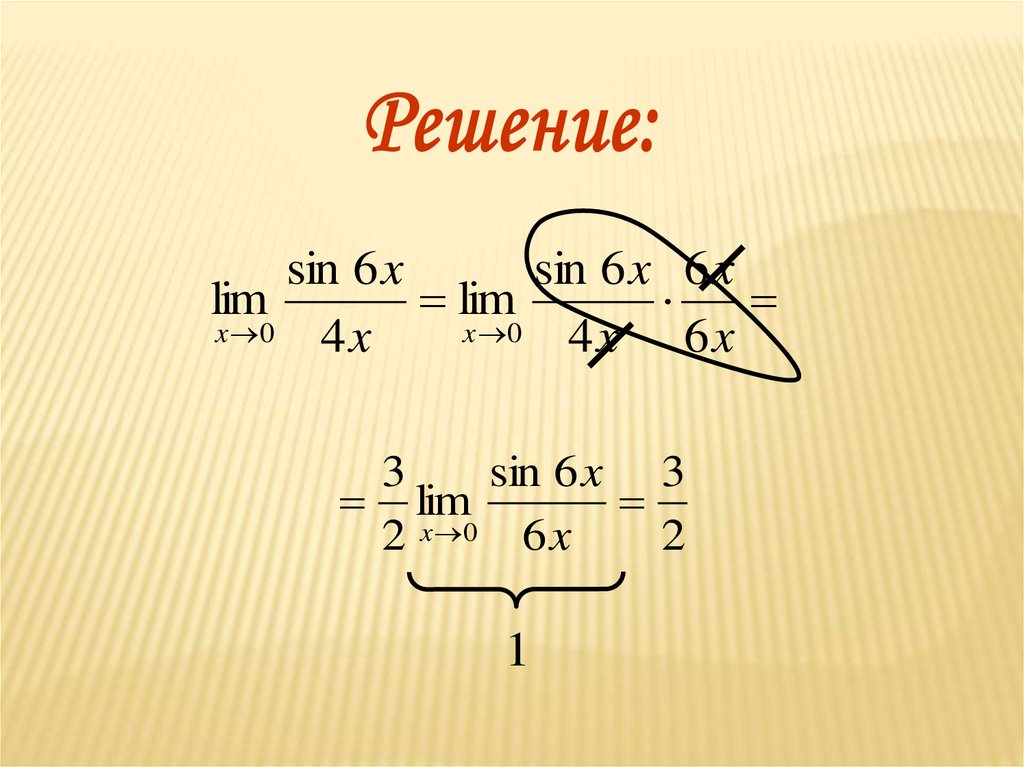
1Вычислить
sin 6 x
lim
x 0
4x
37.
sin 6 xsin 6 x 6 x
lim
lim
x 0
x 0
4x
4x 6x
3
sin 6 x 3
lim
2 x 0 6 x
2
1
38.
2Вычислить
1 cos x
lim
2
x 0
x
39.
x2
sin
1 cos x
2
lim
lim
2
2
x 0
x 0
x
x
2
2
x
sin 1 1
2
lim
2
x 0
x 4 2
2
40.
Числом е или вторым замечательнымпределом называется предел
числовой последовательности
n
1
lim
1
e
n
n
41.
е – число Эйлерае=2,718281…
Можно показать, что функция
при x
1
f ( x) 1
x
x
где х пробегает все значения, а не
только целые, тоже имеет предел,
равный е:
42.
x1
lim
1
e
x
x
1
Пусть y
x
,
тог
да
lim 1 y e
y 0
1
y
43.
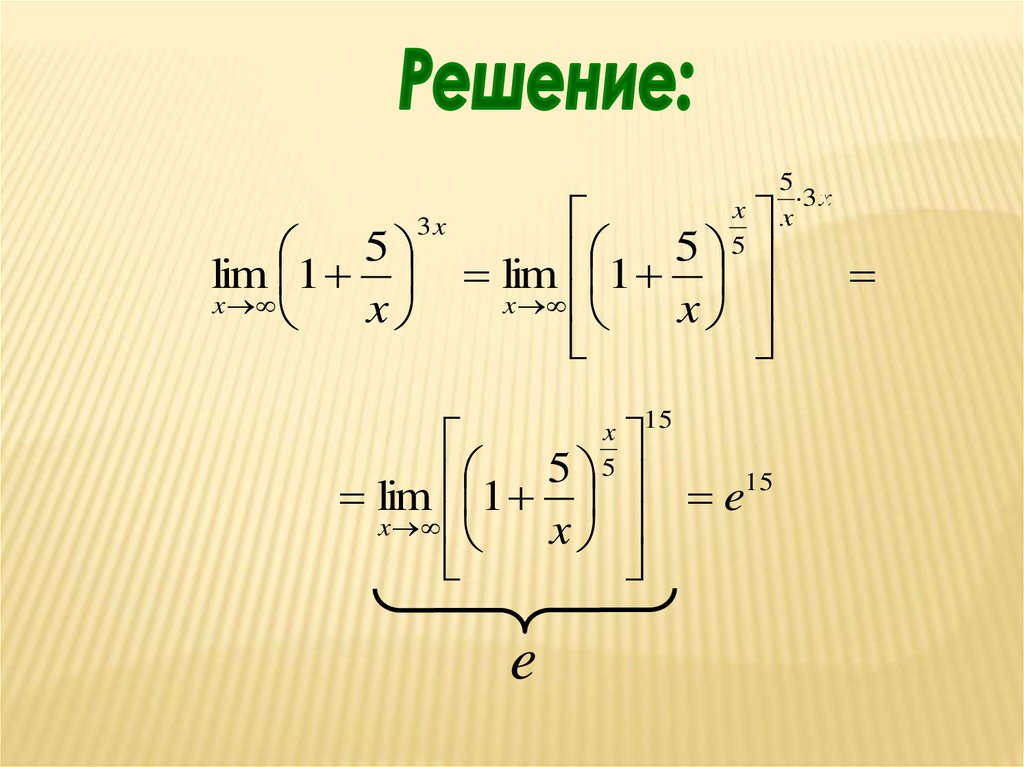
1Вычислить
5
lim 1
x
x
3x
44.
5lim 1
x
x
3x
x
5
5
lim 1
x
x
5
lim 1
x
x
x
5
e
15
e15
5
3 x
x
45.
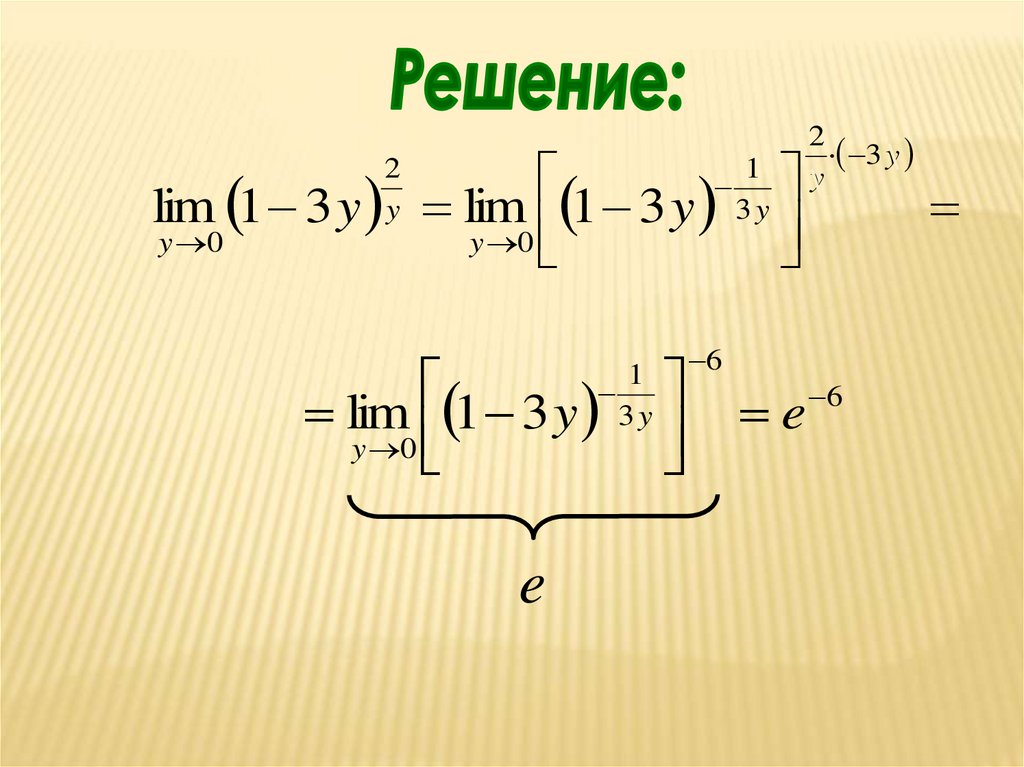
2Вычислить
lim
1
3
y
y 0
2
y
46.
lim 1 3 yy 0
2
y
1
lim 1 3 y 3 y
y 0
lim 1 3 y
y 0
1
3y
e
2
3 y
y
6
e
6







































 Математика
Математика








