Похожие презентации:
Пределы
1. Пределы Составитель: Станкевич Виктория, Руководитель: Коренюгина Людмила Михайловна
2. Понятие предела функции
• Определение: Пределомфункции y= f(x)
называется
некоторое число b
при x→a.
• И записывается
это так :
lim f (x) b
x a
3. Геометрический смысл предела
Определение: Для любого ε>0можно указать δокрестность точки а на
оси Ох ,такую что для всех
х из этой окрестности
кроме х=а,
соответствующее
значение y лежат в εокрестности точки b
Математическая запись:
При |x-a|<δ выполняется |f(x)-b|<ε
-δ<x-a< δ ↔ -ε<f(x)<ε
a-δ<x<a+δ ↔ b-ε<f(x)<b+ε
xЄ(a-δ;a+δ) ↔ f(x)Є(b-ε; b+ε)
4. Геометрический смысл предела (продолжение)
• Если число b1 есть предел функции y= f(x) приx→a, так что x<0, то число b1 называется левым
lim f ( x) b1
односторонним пределом точки а:
x a 0
• Если число b2 есть предел функции y= f(x) при x→a,
так что x>0 то число b2 называется правым
односторонним пределом точки а:
lim f ( x) b2
x a 0
• Если b1=b2=b, то число b есть предел этой функции
при x→a:
lim f ( x) b
x a
5. Бесконечно малые и большие функции и их свойства
• Определение: Функция f(x) называетсябесконечно малой при x→a
x если
предел
этой функции
lim f ( x) 0
x a( x )
• Определение: Функция f(x) называется бесконечно
x этой
0 функции
большой при x→a
если предел
lim f ( x)
x a ( x 0 )
6. Свойства бесконечно малых и больших функции
• Функция обратная по величине бесконечно большой,есть бесконечно малая
lim x 0
x 0
1
lim
x 0 x
• Функция обратная по величине бесконечно малой, но
отличная от 0, есть бесконечно малая
lim x
x
1
lim 0
x x
7. Основные теоремы о пределах
Теорема 1: Для того, чтобы число А было пределом функции f(x) при, необходимо и достаточно, чтобы эта функция была представлена в
виде x a
, где
- бесконечно малая.
(x )
f ( x) A ( x)
Следствие 1: Функция не может в одной точке иметь 2 различных
предела.
Теорема 2: Предел постоянной величины равен самой постоянной
Теорема 3: Если функция
для всех x в некоторой
окрестности точки a, кроме, быть может, самой точки a, и в точке a
имеет предел , то
f ( x) 0( f ( x) 0)
lim f ( x) 0 lim f ( x) 0
x a
x a
8. Основные теоремы о пределах (продолжение)
Теорема 4: Если функция f1(x) и f2(x) имеют приделы при, x a
то при x a, имеет пределы также их сумма f1(x)+f2(x),
произведение f1(x)*f2(x), и при условии lim f 2 ( x) 0 частное
f1(x)/f2(x), причем
lim ( f1 ( x) f 2 ( x)) lim f1 ( x) lim f 2 ( x),
x a
x a
x a
lim ( f1 ( x) f 2 ( x)) lim f1 ( x) lim f 2 ( x),
x a
lim
x a
x a
x a
f1 ( x)
lim f1 ( x) / lim f 2 ( x).
x a
f 2 ( x) x a
Следствие 2: Если функция f(x) имеет предел при x a
, то
lim ( f ( x)) n (lim f ( x)) n ,где n – натуральное число.
x a
x a
Следствие 3: Постоянный множитель можно выносить за знак предела
lim Cf ( x) C lim f ( x), C - const
x a
x a
9. Неопределенности и методы их решений Неопределенность вида
Неопределенности и методы их решений0
Неопределенность вида
0
Методы:
1. Разложение числителя и знаменателя на
множители с последующим сокращением
2. Устранение иррациональных разностей.
Домножение на сопряженное.
3. Первый замечательный предел.
lim
0
sin
1
10. Неопределенности и методы их решений Неопределенность вида
Методы: Деление на наибольшую степень
Предел отношения двух многочленов (при условии, что
аргумент стремится к ∞) равен пределу отношения их
старших членов.
a0 x m a1 x m 1 ... am
a0 x m
lim
lim
n
n
1
x b x b x
x b x n
...
b
0
1
n
0
Здесь a 0 0 и b 0 0
0 (m n)
a0
(m n)
b0
(m n)
11. Примеры:
x 3x 2lim
x 1
x 1
3
1 x 1 x
lim
x 0
1 x 1
sin 7 x
lim
x 0 sin 14 x
2
3n n 1
lim 4
n n 2n
3
12.
Пусть f(x) и φ(x) – функции, для которыхсуществуют пределы при
x x0
или
x
lim
f
(
x
)
A
x x
lim
(
x
)
B
x x
x
x
0
0
Тогда справедливы следующие теоремы:
13.
ТЕОРЕМА 1.Функция не может иметь более
одного предела.
14.
Доказательство:Предположим обратное: что функция f(x) имеет
два предела: А и D, A D
lim
f
(
x
)
A
x x
lim
f
(
x
)
D
x x
x
x
0
0
Тогда функцию f(x) можно представить как
сумму:
f ( x) ( x) A или f ( x) ( x) D
Где ( x), ( x) - бесконечно малые величины
при
x x0 или x
15.
Вычитаем почленно эти равенства:0 A D ( x) ( x)
D A ( x) ( x)
Но по условию теоремы A
D,а разность
( x) ( x)
является
бесконечно
малой
величиной.
Следовательно,
предположение
о
существовании второго предела неверно, и
функция имеет единственный предел.
16.
Предел алгебраической суммы(разности) конечного числа функций
равен сумме (разности) пределов этих
функций:
lim
f
(
x
)
(
x
)
lim
f
(
x
)
lim
(
x
)
A
B
x x
x x
x x
0
0
0
x
x
x
17.
По условию теоремы: limx x
0
x
f ( x) A
lim
( x) B
x x
0
x
Тогда функции f(x) и φ(x) можно представить
как суммы:
f ( x) ( x) A и ( x) ( x) B
Где ( x), ( x) - бесконечно малые величины
при
x
x x или
0
Складываем почленно эти равенства:
18.
f ( x) ( x) A B ( x) ( x)Сумма бесконечно малых величин является
величиной бесконечно малой.
Таким
образом,
функция
f(x)
+
φ(x)
представляет собой сумму числа А+В и
бесконечно малой величины, следовательно
lim
f
(
x
)
(
x
)
A
B
x x
0
x
19.
Предел произведения конечногочисла функций равен произведению
пределов этих функций:
lim f ( x) ( x) lim f ( x) lim ( x) A B
x x0
x x0
x x0
x
x
x
20.
limC
f
(
x
)
C
lim
f
(
x
)
C
A
x x
x x
0
0
x
x
21.
Предел частного двух функций равенчастному пределов этих функций:
lim
f
(
x
)
x x
0
f ( x ) x
A
lim
x x
(
x
)
lim
(
x
)
B
x
x x
0
0
x
22.
Еслиlim f (u) A
u u0
и
lim ( x) u0
x x0
то
предел
сложной
существует и равен
lim f ( x) A
x x0
функции
23.
Если в некоторой окрестноститочки х0 (или при достаточно
больших х) f ( x) ( x) то
lim
f
(
x
)
lim
(
x
)
x x
x x
0
0
x
x
24.
ЗамечаниеВ этих теоремах полагается, что существуют
пределы функций f(x) и φ(x), из чего следует
существование пределов суммы, произведения или
частного этих функций.
Однако из существования пределов суммы, произведения
или частного еще не следует, что существуют пределы
самих функций f(x) и φ(x).
25.
lim tgx ctgx lim 1 1x
Но:
x
2
lim tgx
x
2
2
- не существует
























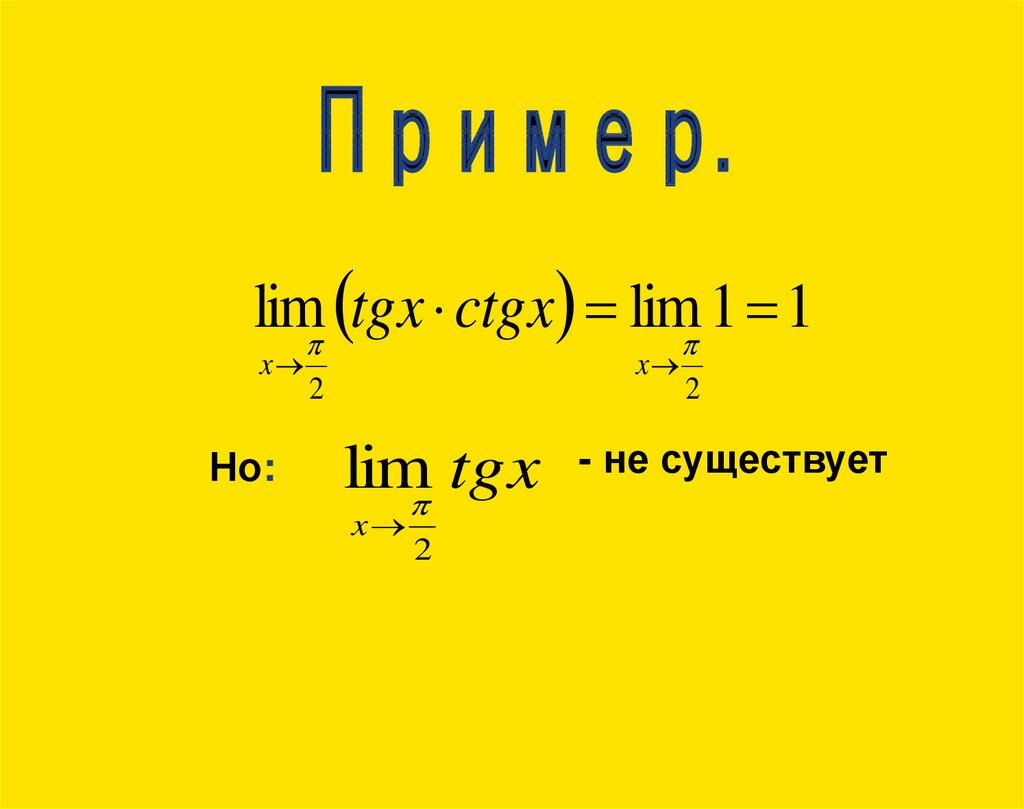



 Математика
Математика








