Похожие презентации:
Энергия электрического поля. Тема 6
1. Омский государственный технический университет Кафедра физики
Калистратова Л.Ф.Электронные лекции по разделам
электромагнетизма
(электростатика, постоянный ток, магнетизм)
17 лекций
(34 аудиторных часа)
2. Тема 6. ЭНЕРГИЯ ЭЛЕКТРИЧЕСКОГО ПОЛЯ
План лекции1. Энергия системы точечных зарядов.
2. Энергия заряженных проводников и конденсаторов.
3. Энергия электростатического поля.
3. 1. Энергия системы точечных зарядов
Рассмотрим два неподвижных точечных заряда q1 и q2,расположенные на некотором расстоянии друг от
друга.
Каждый из зарядов находится в электростатическом
поле, созданном другим зарядом.
Выразим энергию их взаимодействия.
4.
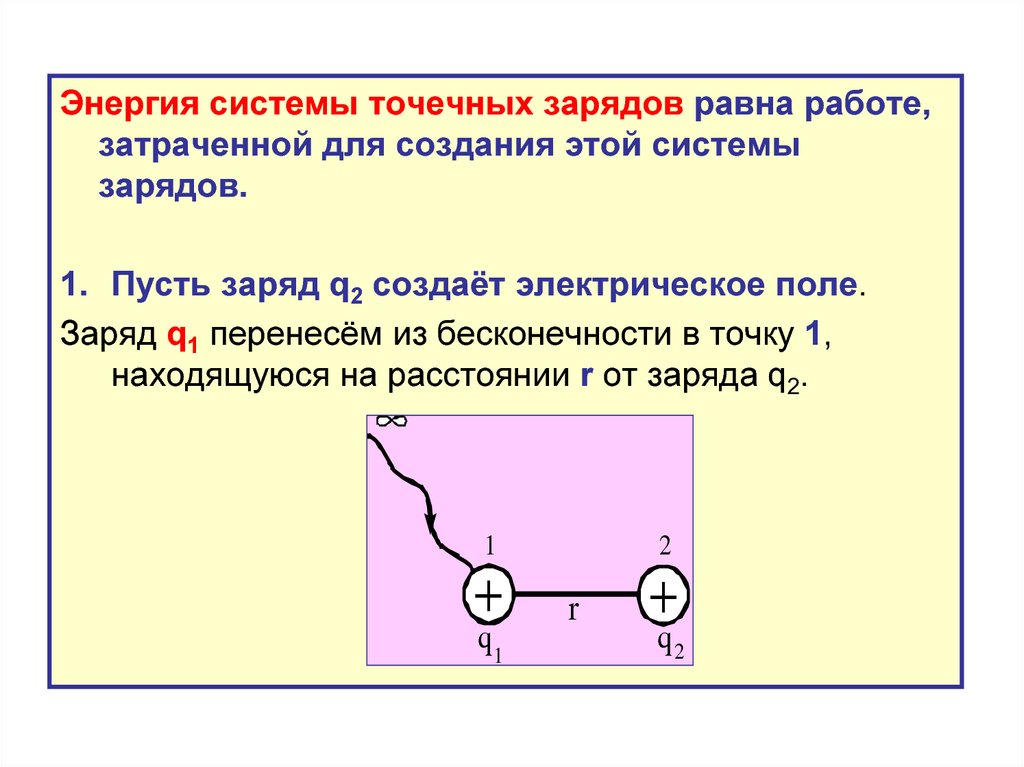
Энергия системы точечных зарядов равна работе,затраченной для создания этой системы
зарядов.
1. Пусть заряд q2 создаёт электрическое поле.
Заряд q1 перенесём из бесконечности в точку 1,
находящуюся на расстоянии r от заряда q2.
.
1
+
q1
2
r
+
q2
5.
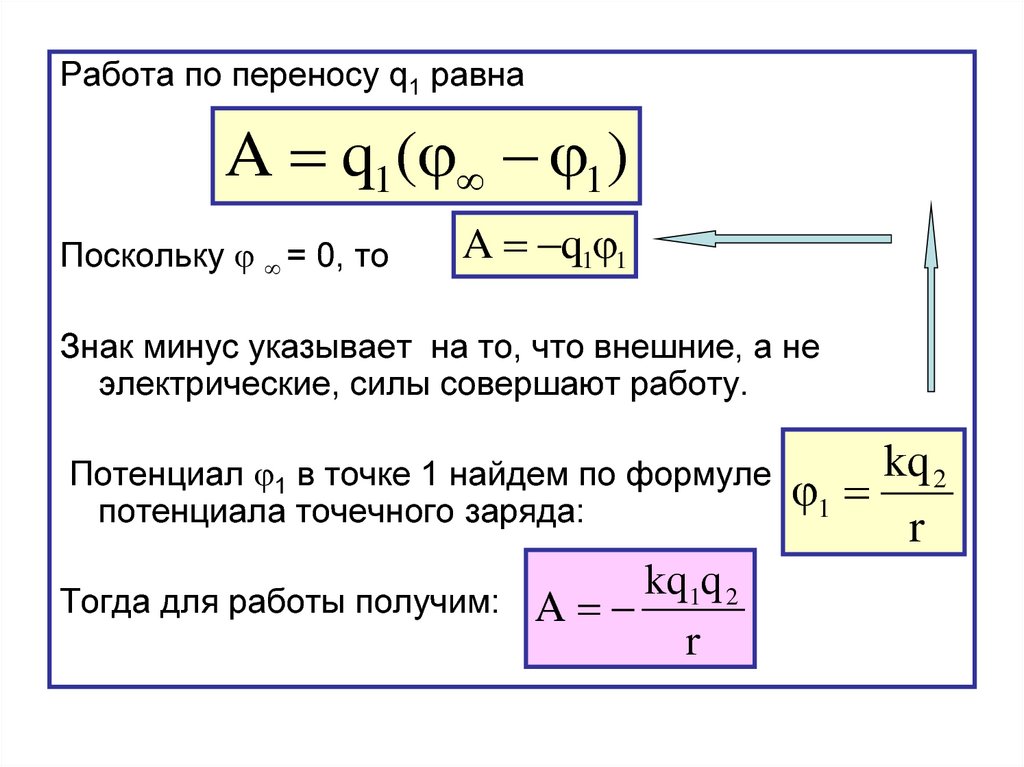
Работа по переносу q1 равнаA q1 ( 1 )
Поскольку = 0, то
A q1 1
Знак минус указывает на то, что внешние, а не
электрические, силы совершают работу.
Потенциал 1 в точке 1 найдем по формуле
потенциала точечного заряда:
Тогда для работы получим:
kq1q 2
A
r
kq 2
1
r
6.
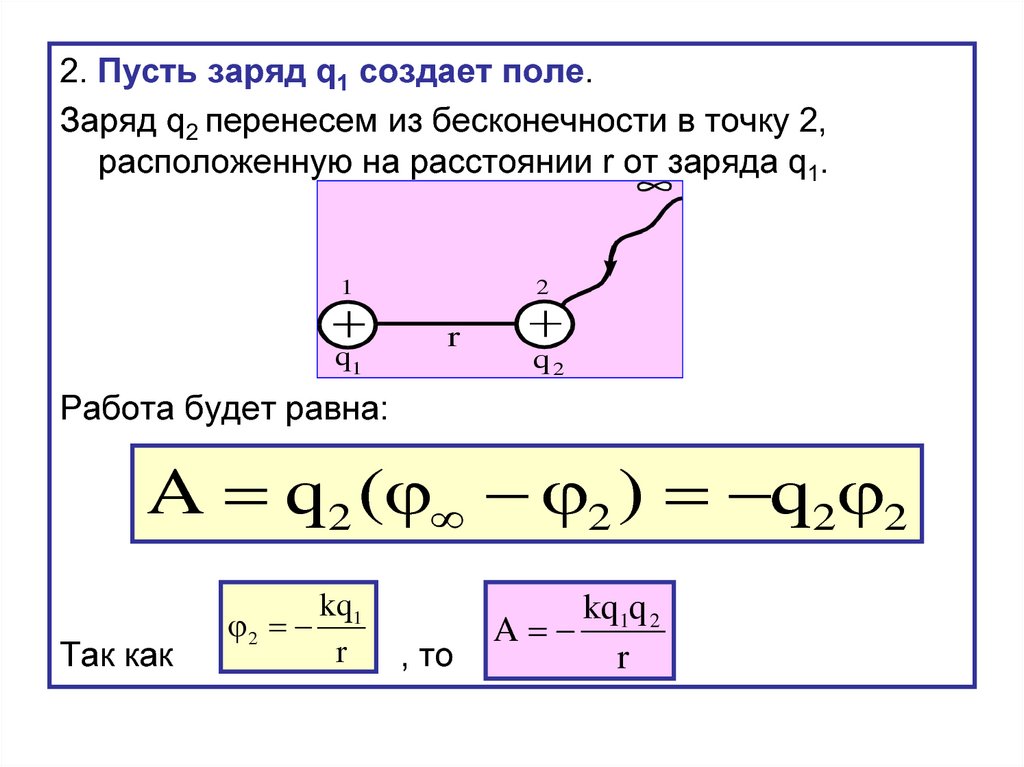
2. Пусть заряд q1 создает поле.Заряд q2 перенесем из бесконечности в точку 2,
расположенную на расстоянии r от заряда q1.
1
q1
2
r
q2
Работа будет равна:
A q2 ( 2 ) q2 2
Так как
2
kq1
r
, то
kq1q 2
A
r
7.
В обоих случаях формулы для вычисления работыполучились одинаковыми, независимо от условий
создания системы двух зарядов:
kq1q 2
A
r
Из механики известно, что работа равна изменению
потенциальной энергии, взятому с обратным знаком:
A W W1 W2
A W2
W1 - потенциальная энергия двух зарядов,
расположенных на бесконечном расстоянии: W1 = 0.
W2 - потенциальная энергия двух зарядов,
расположенных на расстоянии r.
8.
Потенциальная энергия взаимодействия двухточечных зарядов, расположенных на расстоянии r:
kq1q 2
Wn
r
Эту формулу можно записать по-другому, взяв только
по половине от выражений для работ:
A q1 1
A q 2 2
1
Wn (q1 1 q 2 2 )
2
9.
Последнюю формулу можно обобщить для системымногих зарядов, записав ее в виде:
n
1
Wn q i k
2 i 1
В формуле:
i – номер заряда,
qi – величина i-ого заряда,
k – потенциал, созданный всеми зарядами, кроме i-ого
в точке нахождения i-ого заряда.
10. 2. Энергия заряженного проводника и конденсатора
Собственная энергия заряженного проводникаЗаряд, находящийся на заряженном проводнике, можно
рассматривать как систему взаимодействующих
между собой точечных зарядов.
Такая система обладает потенциальной энергией.
Собственная энергия проводника - потенциальная
энергия, которой обладает заряженный
проводник в отсутствие внешнего электрического
поля.
11.
Будем заряжать проводник, перенося заряды малымипорциями dq с нулевого уровня потенциала на
поверхность проводника.
Пусть очередная порция dq переносится, когда на
проводнике уже имеется заряд q и проводник
обладает потенциалом φ.
Элементарная работа по переносу заряда dq из
бесконечности на проводник равна:
dA dq( )
Потенциал в бесконечности равен нулю.
Отрицательную работу внешних сил заменим
положительной работой электрических сил поля
заряженного проводника.
dA dq
12.
Полная работа А вычисляется какq
A dq
0
В интегральное выражение подставим потенциал,
выраженный через электроёмкость:
q
C
Тогда работа А и, соответственно, собственная
энергия заряженного проводника W определяются
выражениями:
q
2
q
q
A dq
C
2C
0
2
q
W
2C
13.
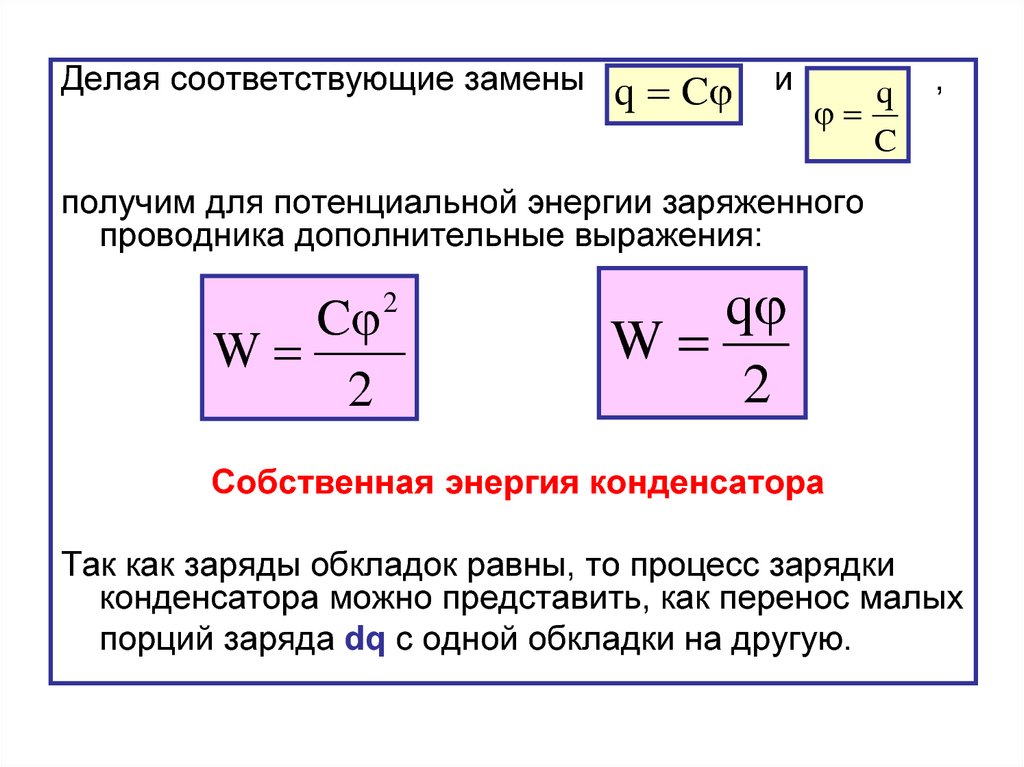
Делая соответствующие замены q Cи
q
C
,
получим для потенциальной энергии заряженного
проводника дополнительные выражения:
C 2
W
2
q
W
2
Собственная энергия конденсатора
Так как заряды обкладок равны, то процесс зарядки
конденсатора можно представить, как перенос малых
порций заряда dq с одной обкладки на другую.
14.
Элементарная работа, совершаемая силами поля припереносе заряда dq равна:
dA dq 1 2 dq d
Перейдём к вычислению потенциальной энергии:
Тогда
W A
2
qdq q
W dqd
C
2C
15.
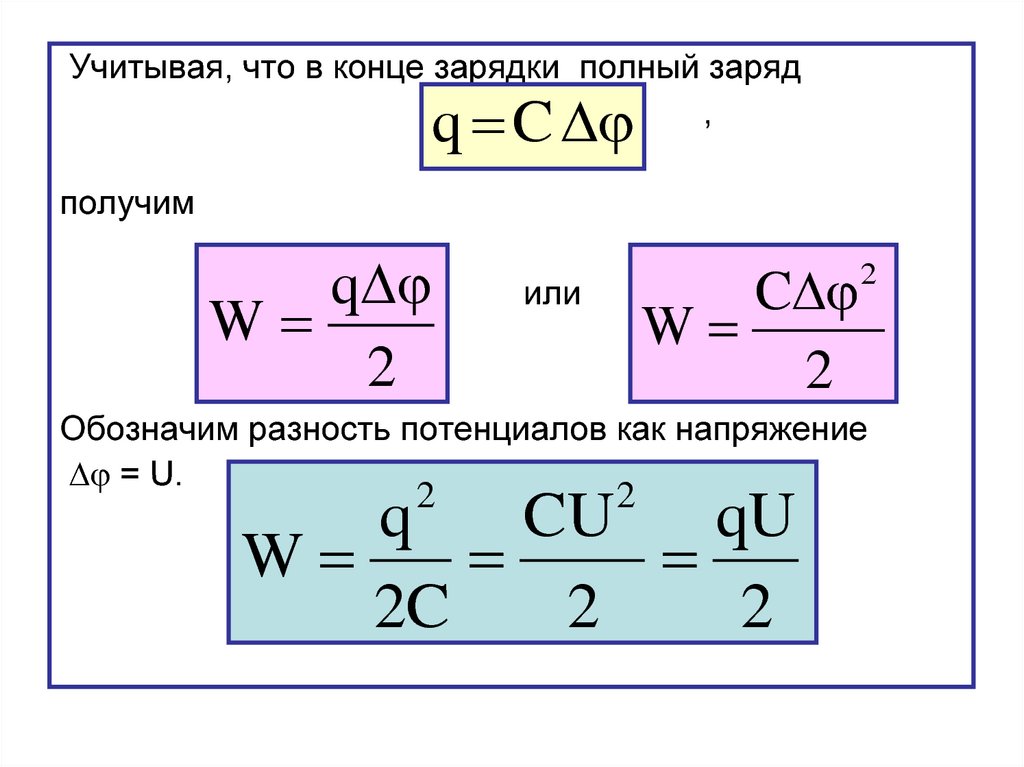
Учитывая, что в конце зарядки полный заряд,
q C
получим
q
W
2
C
W
2
или
2
Обозначим разность потенциалов как напряжение
= U.
2
2
q
CU
qU
W
2C
2
2
16. 3. Энергия электростатического поля
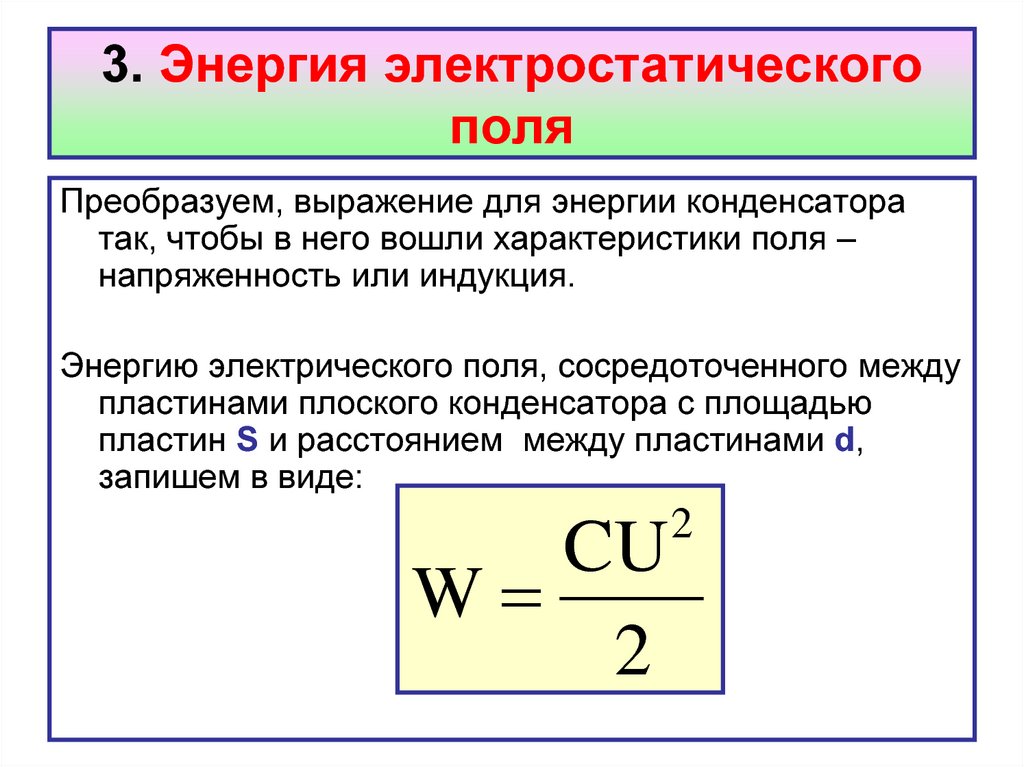
Преобразуем, выражение для энергии конденсаторатак, чтобы в него вошли характеристики поля –
напряженность или индукция.
Энергию электрического поля, сосредоточенного между
пластинами плоского конденсатора с площадью
пластин S и расстоянием между пластинами d,
запишем в виде:
CU
W
2
2
17.
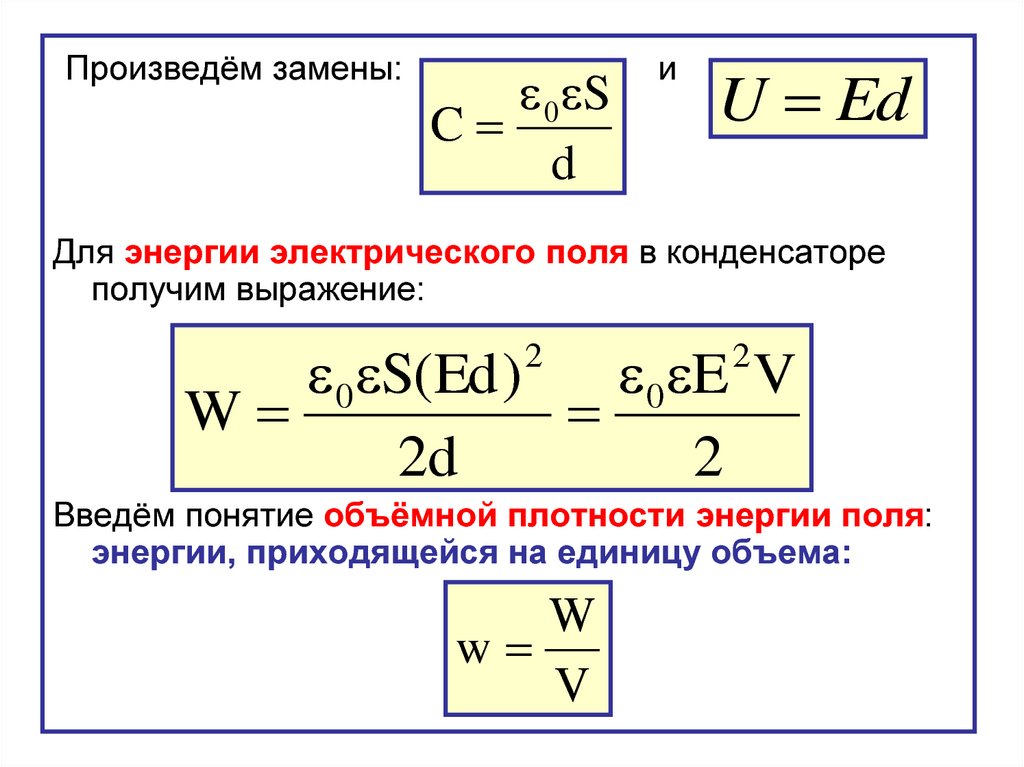
Произведём замены:0 S
C
d
и
U Ed
Для энергии электрического поля в конденсаторе
получим выражение:
0 S(Ed )
0 E V
W
2d
2
2
2
Введём понятие объёмной плотности энергии поля:
энергии, приходящейся на единицу объема:
W
w
V
18.
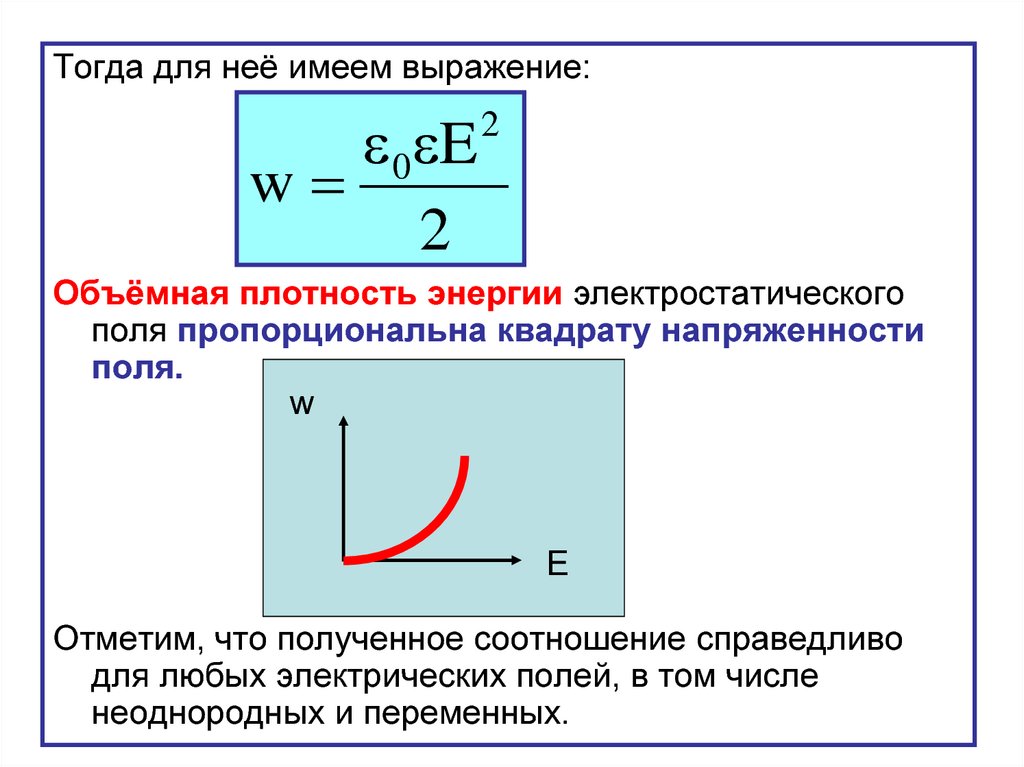
Тогда для неё имеем выражение:0 E
w
2
2
Объёмная плотность энергии электростатического
поля пропорциональна квадрату напряженности
поля.
w
E
Отметим, что полученное соотношение справедливо
для любых электрических полей, в том числе
неоднородных и переменных.
19.
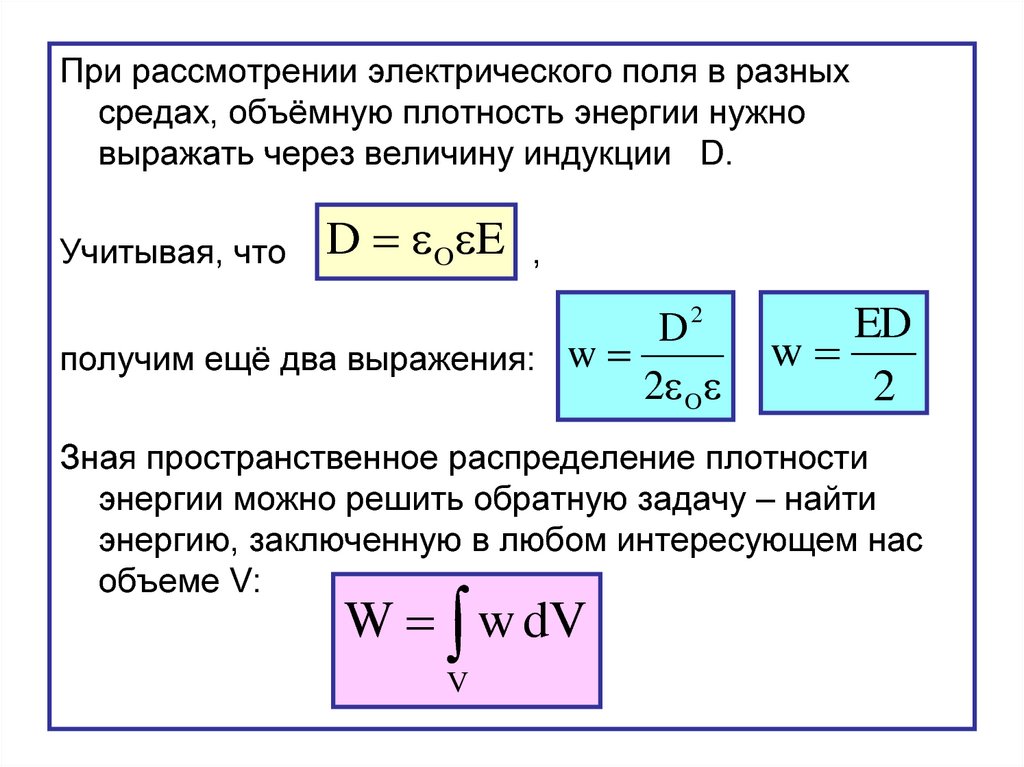
При рассмотрении электрического поля в разныхсредах, объёмную плотность энергии нужно
выражать через величину индукции D.
Учитывая, что
D O E
,
D2
получим ещё два выражения: w
2 O
ED
w
2
Зная пространственное распределение плотности
энергии можно решить обратную задачу – найти
энергию, заключенную в любом интересующем нас
объеме V:
W w dV
V










 Физика
Физика