Пределы и непрерывность

1. Пределы и непрерывность

2. Предел последовательности

3.

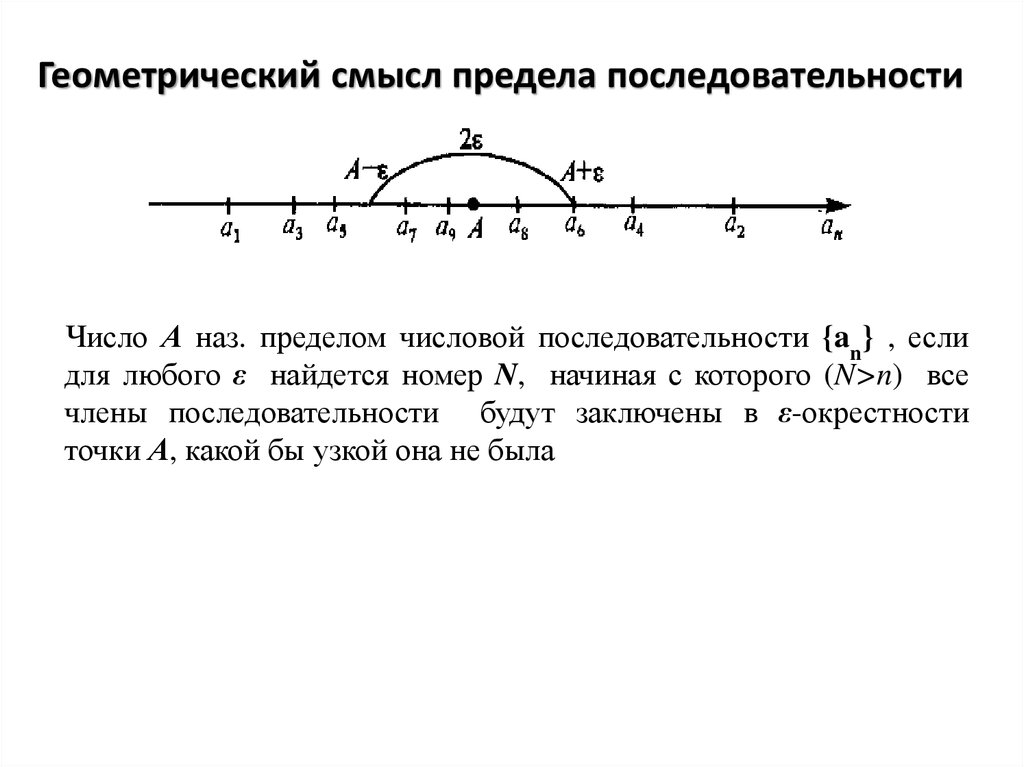
4. Геометрический смысл предела последовательности

Число А наз. пределом числовой последовательности {an} , если
для любого ε найдется номер N, начиная с которого (N>n) все
члены последовательности будут заключены в ε-окрестности
точки А, какой бы узкой она не была

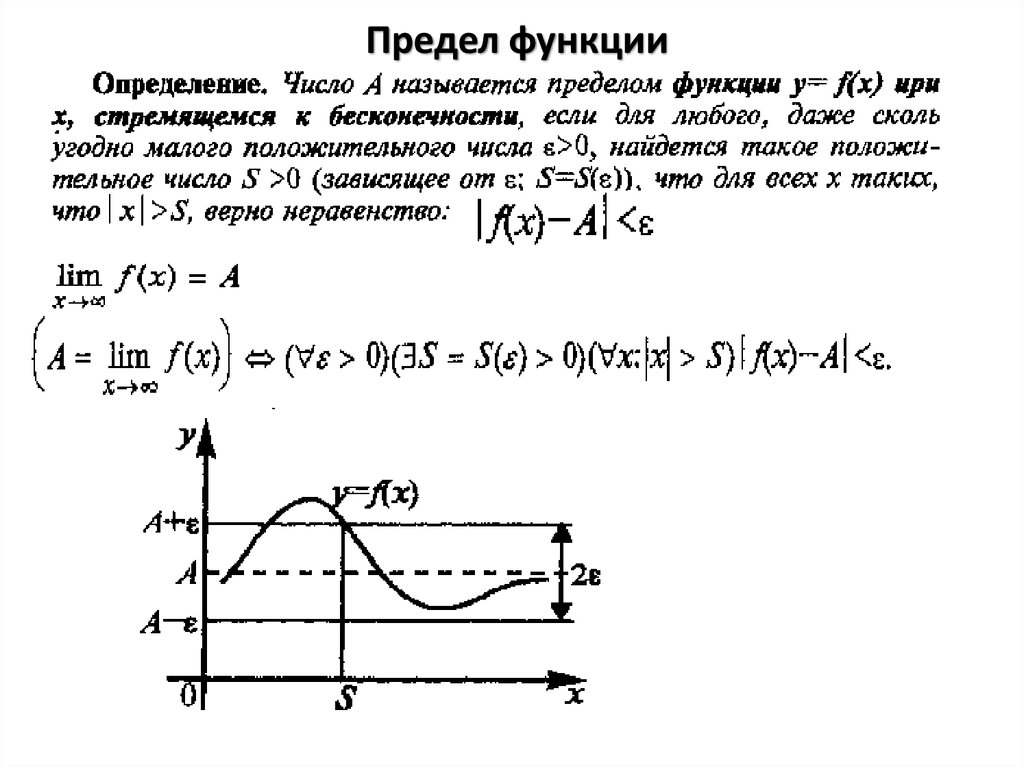
5. Предел функции

6.

7. Бесконечно малые величины

Связь бесконечно малых величин с пределами функций

8. Свойства бесконечно малых величин

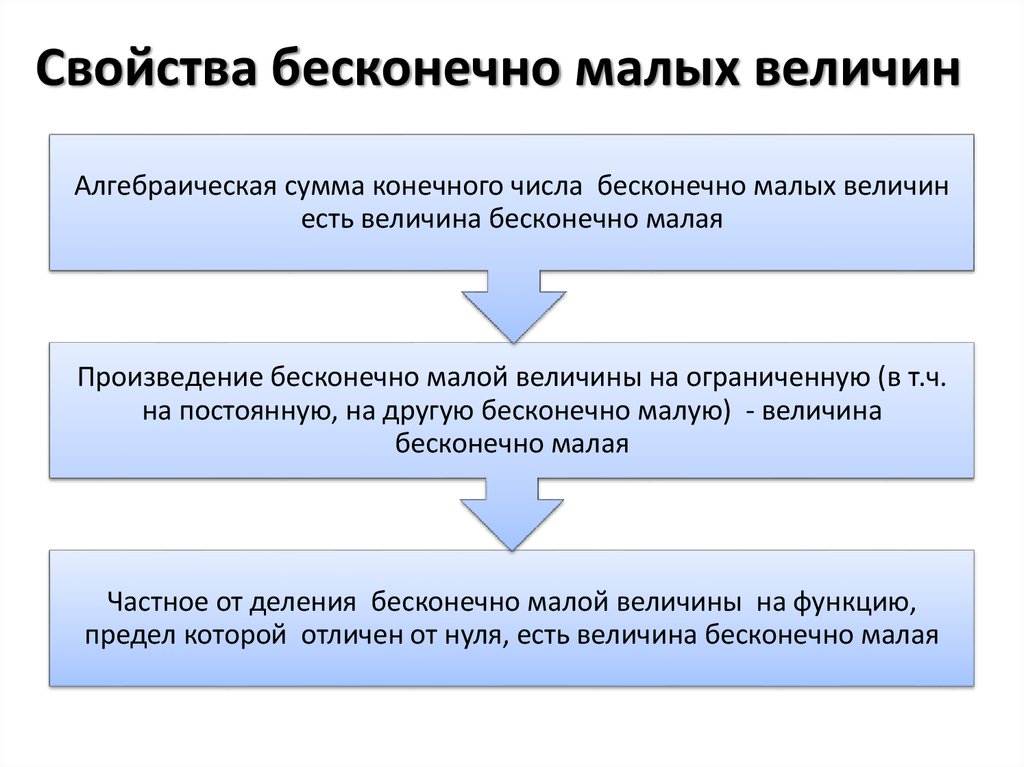
Алгебраическая сумма конечного числа бесконечно малых величин
есть величина бесконечно малая
Произведение бесконечно малой величины на ограниченную (в т.ч.
на постоянную, на другую бесконечно малую) - величина
бесконечно малая
Частное от деления бесконечно малой величины на функцию,
предел которой отличен от нуля, есть величина бесконечно малая

9. Бесконечно большие величины

10. Свойства бесконечно больших величин

Произведение бесконечно большой величины на функцию, предел
которой отличен от нуля, есть величина бесконечно большая
Сумма бесконечно большой величины и ограниченной функции величина бесконечно большая
Частное от деления бесконечно большой величины на функцию,
имеющей предел, есть величина бесконечно большая

11. Связь между бесконечно малыми и бесконечно большими величинами

Если функция
величина при
есть бесконечно малая
, то функция
является бесконечно большой при
И обратно, если функция
большая при
,
то
есть величина
.
бесконечно малая при
.
бесконечно

12. Основные теоремы о пределах.

• Функция не может иметь больше одного предела
• Предел алгебраической суммы конечного числа функций
равен такой же сумме пределов этих функций
• Предел конечного числа функций равен произведению
пределов этих функций.
• Предел частного двух функций равен частному пределу
этих функций

13.

14. Признаки существования предела

15. Замечательные пределы

Первый замечательный предел:
sin x
1
lim
x
x 0
Второй замечательный предел:
n
1
1 e
lim
n
n

16. Эквивалентность

Эквивалентность при х 0:
sinx x
-1 x
tgx x
ln(1+x) x
arcsinx x
arctgx x
sinx² x²
-1 x
1-cosx

17. Эквивалентность может быть записана в терминах БМВ:

sinx=x+o(x), х 0
-1 x+o(x), х 0
tgx=x +o(x), х 0
ln(1+x)=x +o(x), х 0
arcsinx=x +o(x), х 0
arctgx=x+o(x), х 0
=1 x+o(x), х 0