Определенный интеграл

1.

Определенный интеграл
Преподаватель математики
Чебоксарского кооперативного
техникума Чувашпотребсоюза
Мисюк Татьяна Максимовна

2.

Определенный интеграл
b
f ( x)dx F ( x) ba F (b) F (a) - формула Ньютона –
a
Лейбница
a - нижний предел интегрирования,
b-
верхний предел интегрирования.

3.

b
Для вычисления определённого интеграла
f ( x)dx,
a
нужно:
1. Найти какую-нибудь первообразную F (x )
для функции
функции f (x )
(найти неопределенный интеграл от
, в котором можно принять
C=0 );
2. В полученном выражении подставить вместо
сначала верхний предел b
предел
x
, а затем нижний
a , и из результата первой подстановки
вычесть результат второй.

4.

Пример 1
3
4 3
4
4
3
2
81 16 65
1
x
3
2 x dx 4 4 4 4 4 4 16 4
2
Пример 2
sin xdx cos x 0
0
( 2) 2
(cos
cos
0)
1
1
Пример 3
2
dx
1 x ln x
2
1
ln 2 ln
1 ln 2
0

5.

Пример 4
2
3
2
x
3
x
2
(
x
1 3x 7)dx 3 2 7 x 1
2
3
1 3 3 2
1
3
2
2 2 7 2 1 1 7 1
2
2
3
3
8
1 3
6 14 7 19,5
3
3 2
Пример 5
x3 4 x 2
2 x3
2
2
x 2 x x
( x 4 x 1)dx
2
3
1 3
1
1
2
2
3
8
23
1
1
2
2
2
2
2
2 1 1 10 1 12
3
3
3
3
10
1

6.

Замена переменной в
определенном интеграле
При
вычислении определенного
интеграла
способом подстановки новая переменная вводится
подобно случаю неопределенного интеграла. Однако
в отличие от неопределенного интеграла, где в
полученном результате мы снова возвращались к
старой переменной, здесь этого делать не надо,
так как одновременно с заменой переменной
меняются пределы интегрирования.

7.

Пример 6
t 2 x3 1
1
6
1 4
dt
2
x
1
dx
6
x
dx
6
(
2
x
1
)
x
dx
t dt
0
61
x 0 t 1
t
dt
1
3
4
3
2
2
3
x 1 t 3
1 t5
6 5
3
1
t5
30
3
1
35 15 243 1 242
1
8
30 30 30 30 30
15

8.

Пример 7
t 1 2 x3
dt 6 x dx
6 x dx
0 1 2 x 3 x 0 t 1
1
2
2
x 1 t 3
ln t
3
1
0
t sin x
dt cos xdx
6
0
dt
t
1
ln 3 ln
1 ln 3
Пример 8
e
3
sin x
12
cos xdx x 0 t sin 0 0
1
x t sin
6
6 2
e1 2 e 0 e 1
e dt e t
t
0
12
0

9.

Вычисление площадей плоских
фигур
b
S f ( x)dx
a
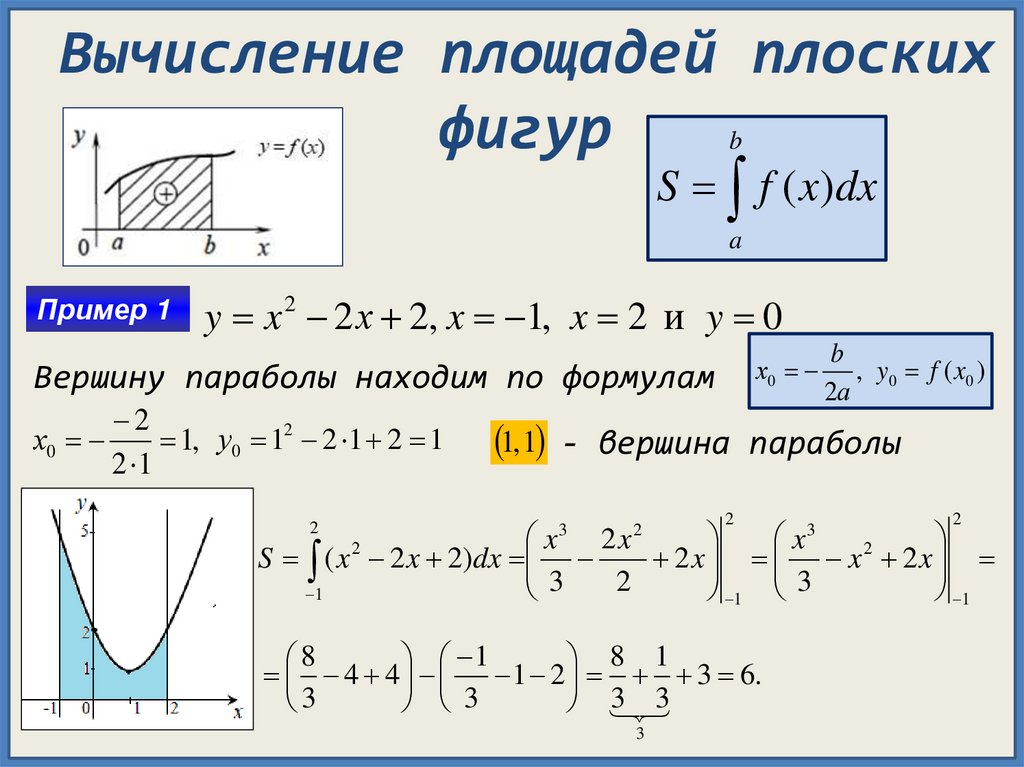
Пример 1
y x 2 2 х 2, x 1, x 2 и y 0
х0
Вершину параболы находим по формулам
2
х0
1, у0 12 2 1 2 1
2 1
b
, y0 f ( x0 )
2а
1, 1 - вершина параболы
2
2
x 2x
x
S ( x 2 2 x 2)dx
2 x x 2 2 x
2
3
1 3
1
1
2
3
2
8
1
8 1
4 4 1 2 3 6.
3
3
3
3
3
3

10.

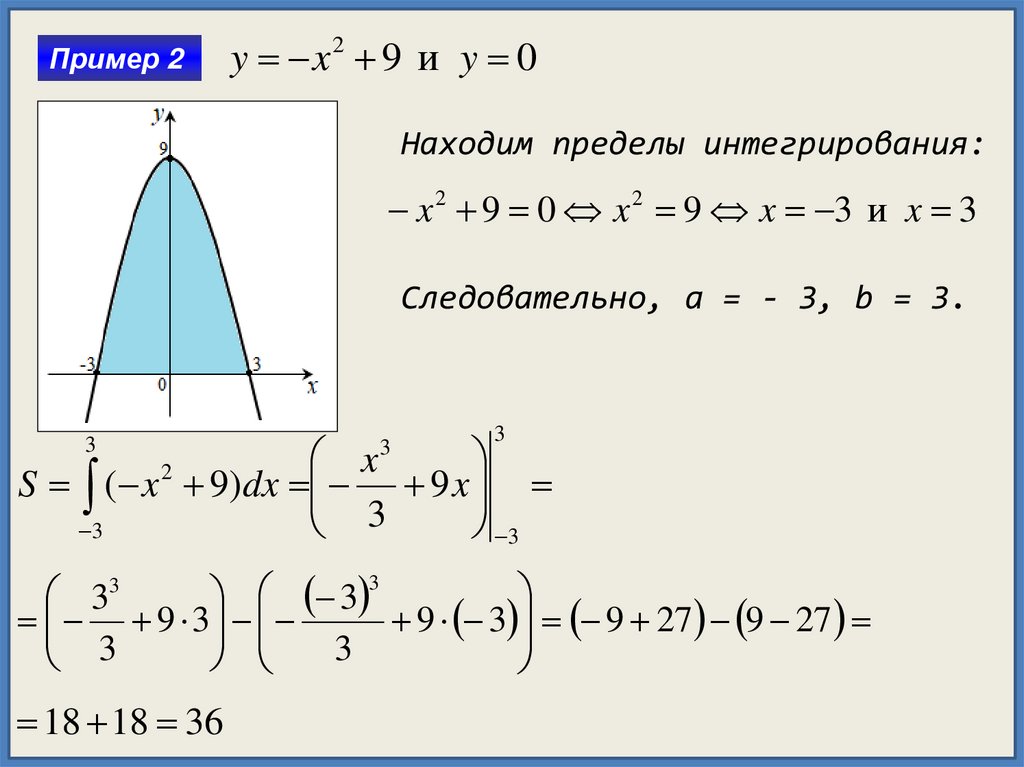
Пример 2
y x2 9 и y 0
Находим пределы интегрирования:
x 2 9 0 x 2 9 x 3 и x 3
Следовательно, a = - 3, b = 3.
3
x
S ( x 9)dx 9 x
3
3
3
3
3
2
33
3 3
9 3
9 3 9 27 9 27
3
3
18 18 36

11.

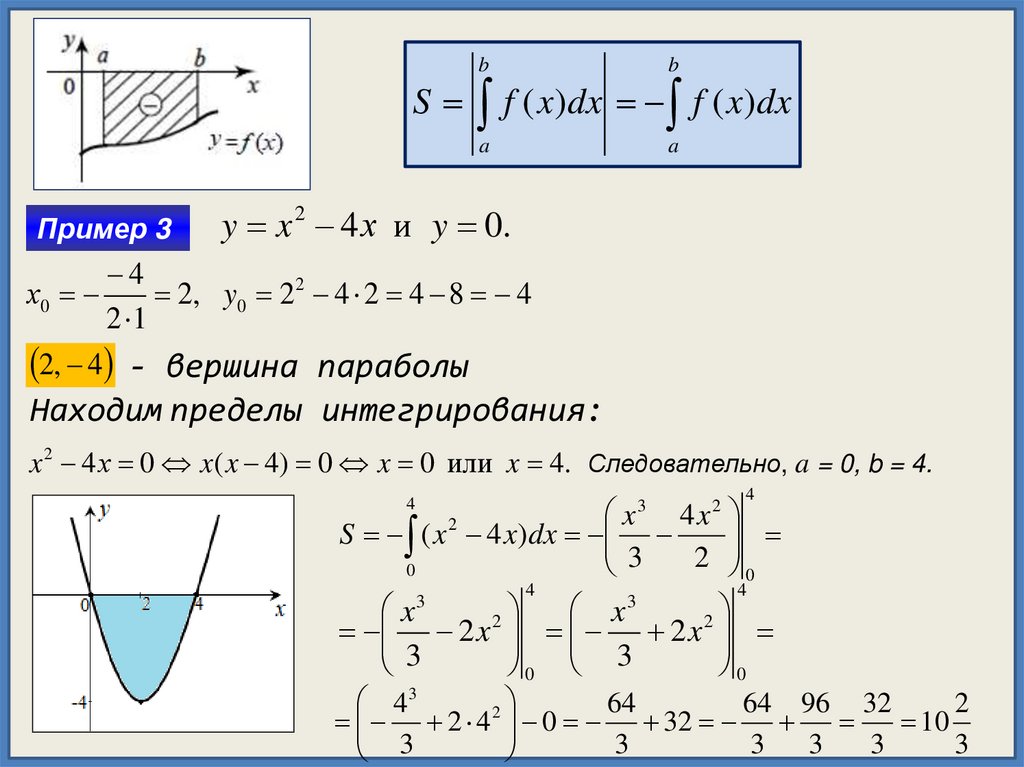
S
Пример 3
х0
b
b
a
a
f ( x)dx f ( x)dx
y x 2 4 х и y 0.
4
2, y0 2 2 4 2 4 8 4
2 1
2, 4 - вершина параболы
Находим пределы интегрирования:
x 2 4 х 0 x( x 4) 0 x 0 или x 4. Следовательно, a = 0, b = 4.
4
x 4x
S ( x 4 x)dx
2 0
3
0
4
3
2
2
4
4
x
x
2
2
2 x 2 x
3
0 3
0
3
3
43
64
64 96 32
2
2
2 4 0 32
10
3
3
3
3
3
3

12.

b
S ( f 2 ( x) f1 ( x))dx
a
Пример 5
y x 2 2 х 8 и y x 6.
2
х0
1, y0 12 2 1 8 9
2 1
1, 9 - вершина параболы.
Находим пределы интегрирования:
x2 2х 8 x 6
x2 2х 8 x 6 0
x2 х 2 0
x1 1 и x2 2 a 1, b 2
y1 1 6 5, y2 2 6 8

13.

1, 5 , 2, 8
- точки пересечения
параболы и прямой
2
3
2
2
x
x
2
S
x
2
x 8
x 6 dx x x 2 dx 2 x
f
(
x
)
3 2
1
f2 ( x)
1
1
1
2
x
23 2 2
1 3 1 2
x
2 x 2 2
2 1
2
3
2
3
1 3 2
3
2
2
8
1 1
1
8
1 1
2 4 2 6 2 5 4,5
3
3 2
2
3
3 2
2

14.

Литература
1)Богомолов Н. В. Практические занятия по
математике: учебное пособие для СПО / Н. В.
Богомолов. – 11-е изд., пер. и доп. — М.:
Издательство Юрайт, 2015. – 495с
2)Математика для экономистов и менеджеров.
Практикум: учебное пособие/ коллектив авторов;
под ред. Н.Ш. Кремера. – М.: КНОРУС, 2017. –
480с.