Производная функции одной переменной. Введение в математический анализ

1.

Производная функции
одной переменной
Введение в математический анализ

2.

План вебинара
1. Разбор ДЗ – ключевые моменты.
2 . Производные функции одной переменной.
+ основы;
+ приближённые (численные) вычисления;
+ производная неявной, обратной, заданной
параметрически функций.
2

3.

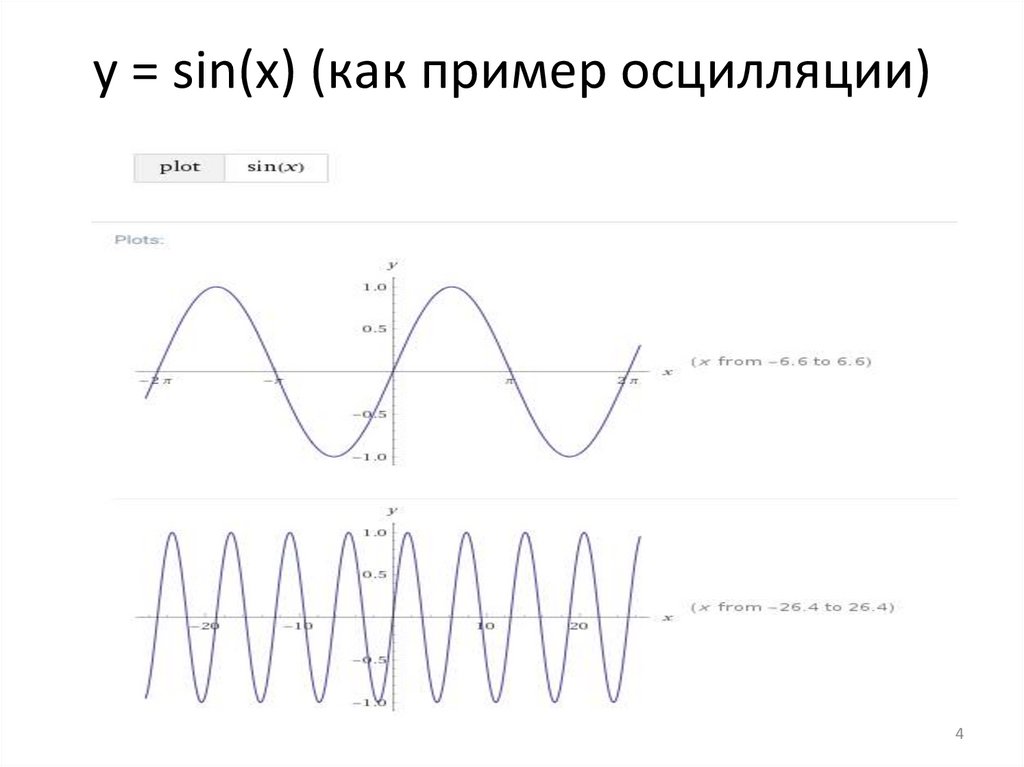
Предложить пример функции, не имеющей
предела в нуле и в бесконечностях.
Есть два вида отсутствия предела функции:
• ꝏ
• осцилляция
3

4.

y = sin(x) (как пример осцилляции)
4

5.

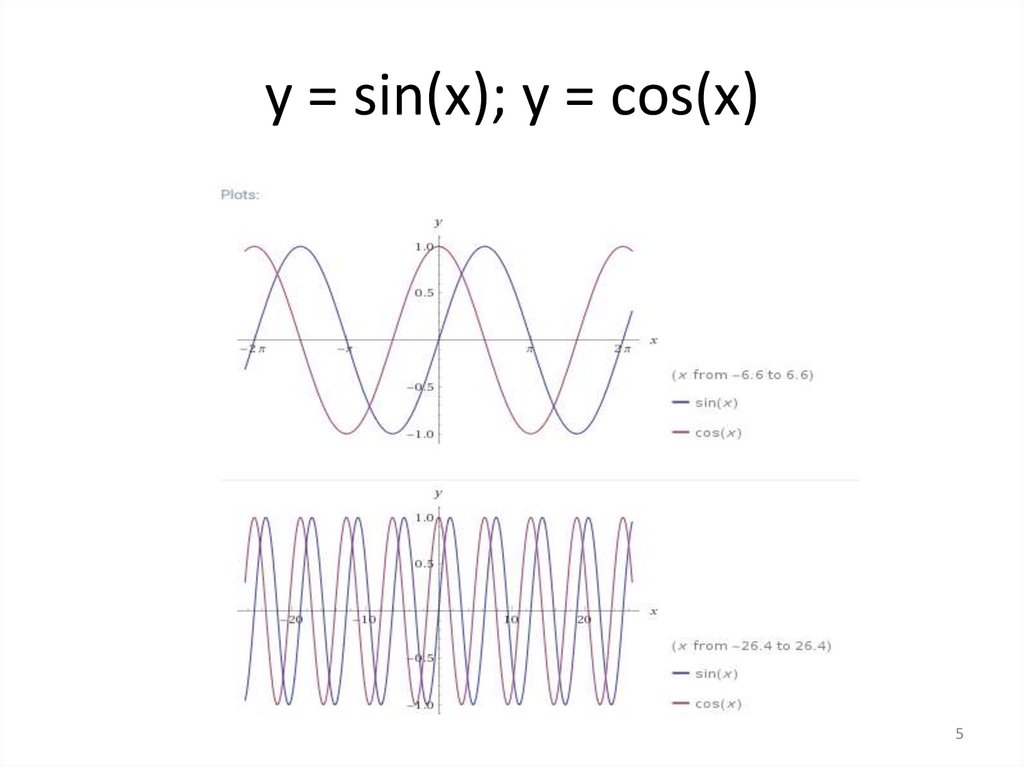
y = sin(x); y = cos(x)
5

6.

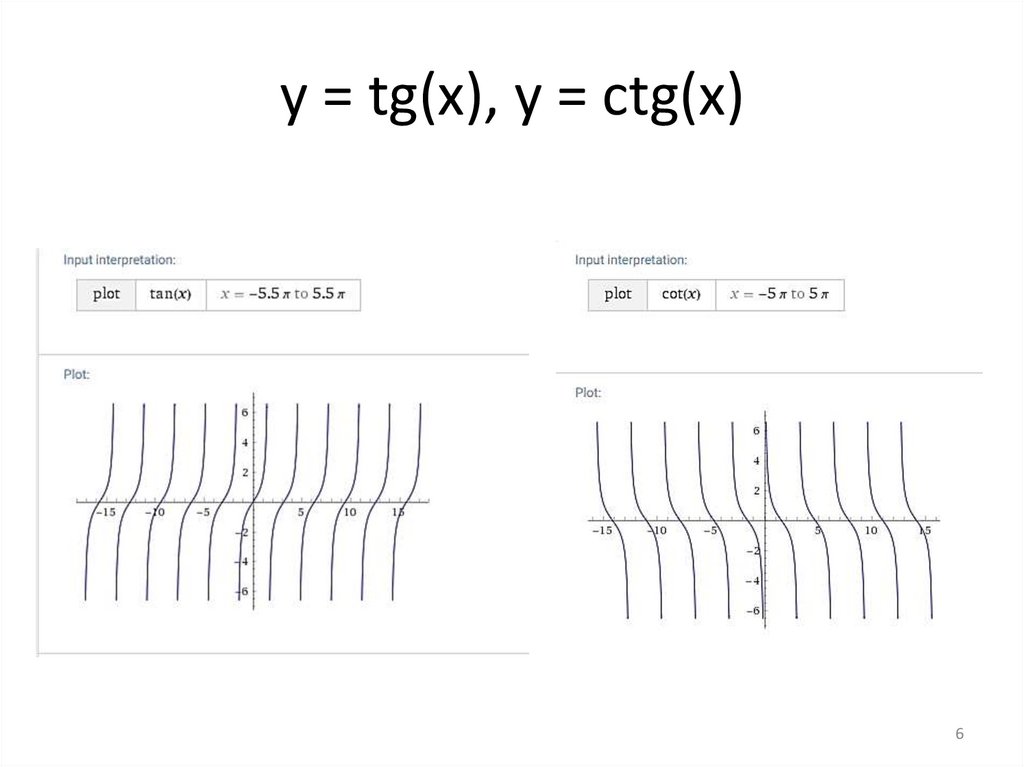
y = tg(x), y = ctg(x)
6

7.

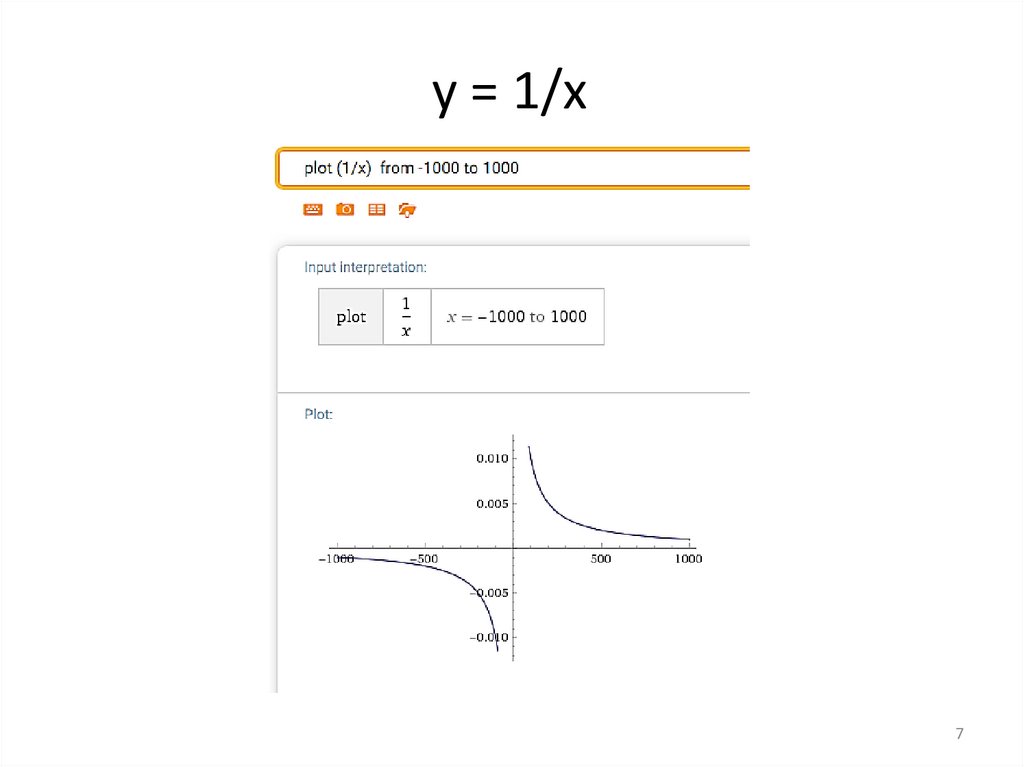
y = 1/x
7

8.

8

9.

Из ДЗ
Монотонность
+убывает
9

10.

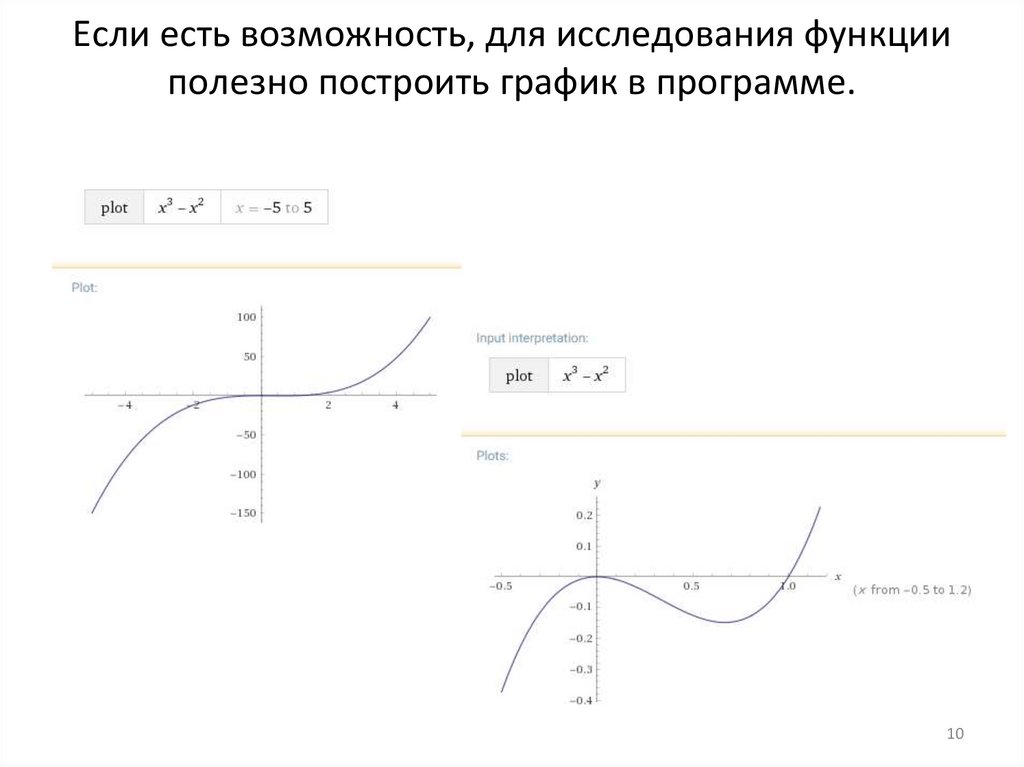
Если есть возможность, для исследования функции
полезно построить график в программе.
10

11.

№4 а, б)
11

12.

Вернёмся
к производным

13.

На прошлом занятии:
1. Определение производной
2. Основные формулы для вычисления производных:
• производная суммы, разности, произведения и
частного функций;
• производная сложной функции.
3. Бонус: Теорема Лопиталя
13

14.

14

15.

Правило Лопиталя
15

16.

Пример применения правила
Лопиталя
16

17.

Пример применения правила
Лопиталя: когда нельзя применять
17

18.

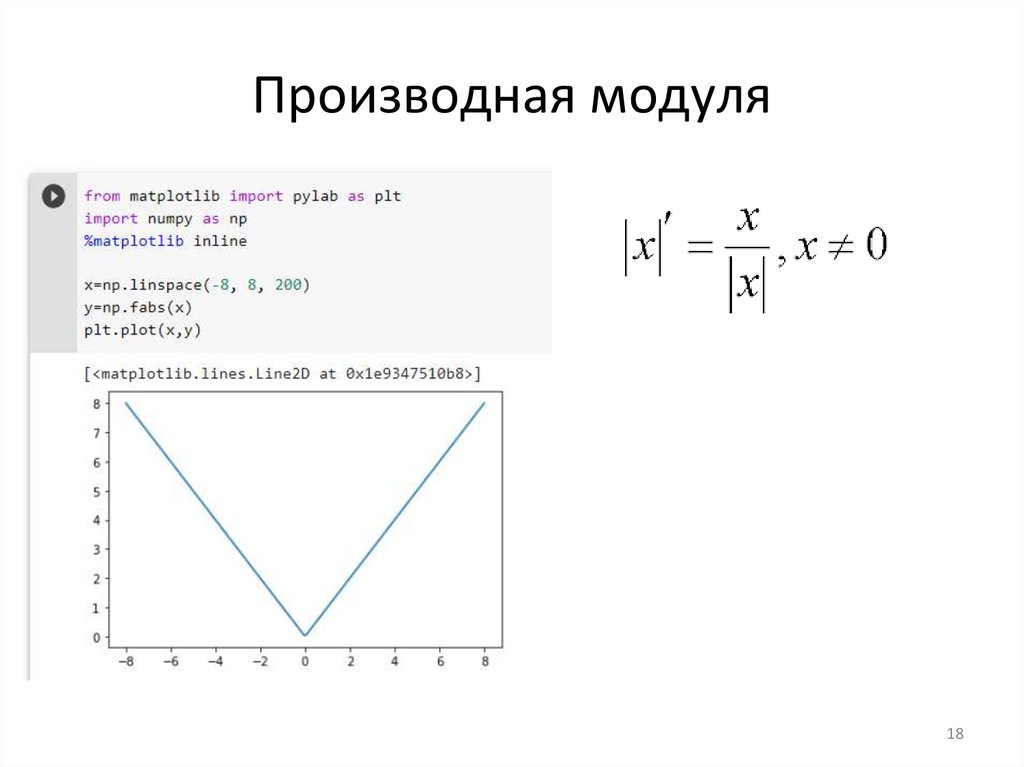
Производная модуля
18

19.

Приближенное вычисление
19

20.

Приближенное вычисление
20

21.

Приближенное вычисление
улучшаем результат
21

22.

22

23.

23

24.

Производная обратной функции
Проверка
24

25.

Производная обратной функции
25

26.

Производная от функции, заданной
параметрически
26

27.

Производная от функции, заданной
параметрически
27

28.

Производная от функции, заданной
параметрически
28

29.

29

30.

30

31.

31

32.

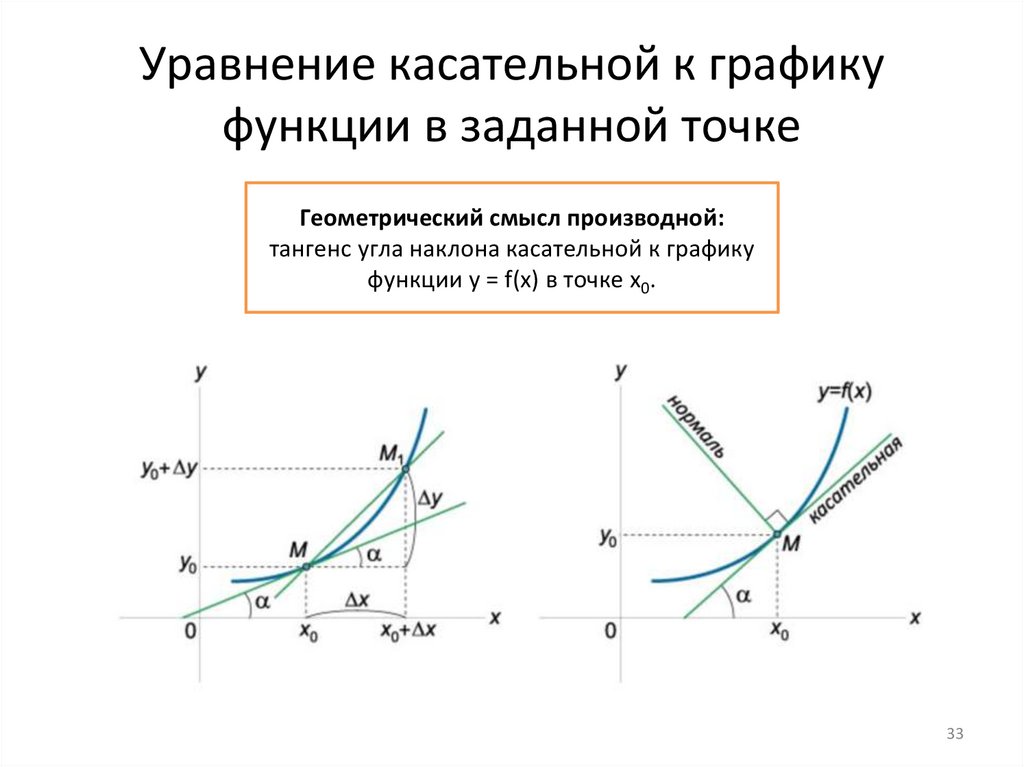
Уравнение касательной к графику
функции в заданной точке
Геометрический смысл производной:
тангенс угла наклона касательной к графику
функции y = f(x) в точке х0.
http://www.math24.ru/%D1%83%D1%80%D0%B0%D0%B2%
D0%BD%D0%B5%D0%BD%D0%B8%D1%8F%D0%BA%D0%B0%D1%81%D0%B0%D1%82%D0%B5%D0
%BB%D1%8C%D0%BD%D0%BE%D0%B9-%D0%B8%D0%BD%D0%BE%D1%80%D0%BC%D0%B0%D0%BB%D
0%B8.html
32

33.

Уравнение касательной к графику
функции в заданной точке
Геометрический смысл производной:
тангенс угла наклона касательной к графику
функции y = f(x) в точке х0.
33

34.

вместо m,
можно b
пожалуйста
сделать
34

35.

Уравнение касательной к графику
функции в заданной точке
Геометрический смысл производной:
тангенс угла наклона касательной к графику
функции y = f(x) в точке х0.
35

36.

Уравнение нормали к графику
функции в заданной точке
Нормаль перпендикулярна касательной.
У перпендикулярных прямых:
36

37.

Пример для явной функции
37

38.

Пример для явной функции
38

39.

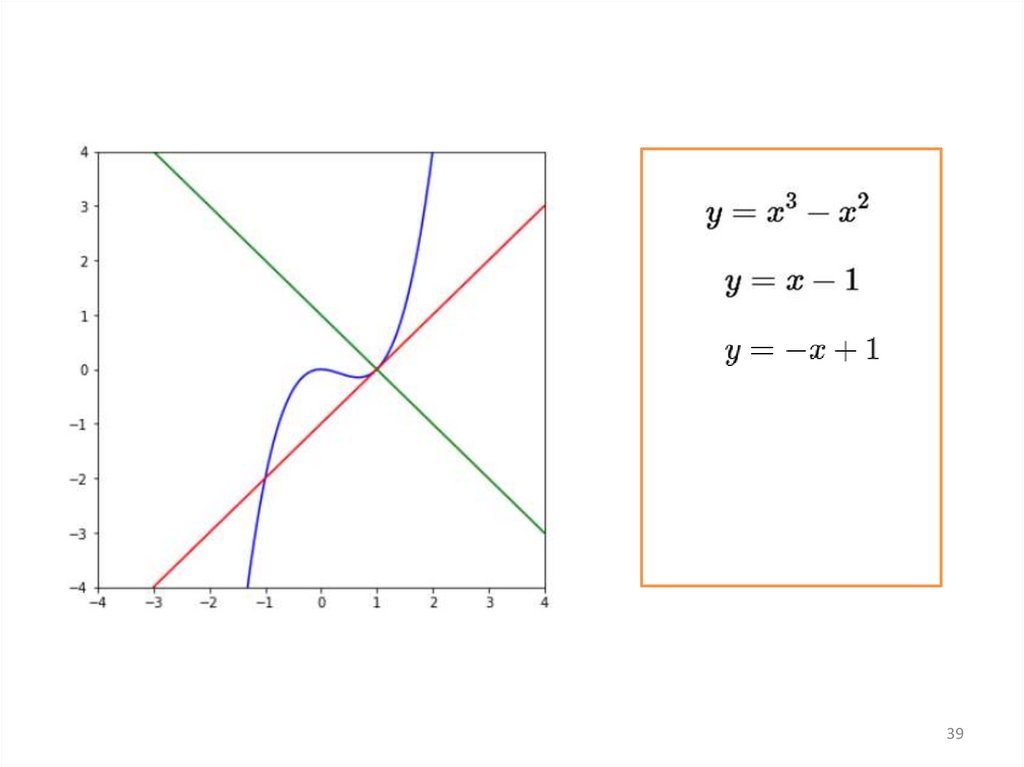
39

40.

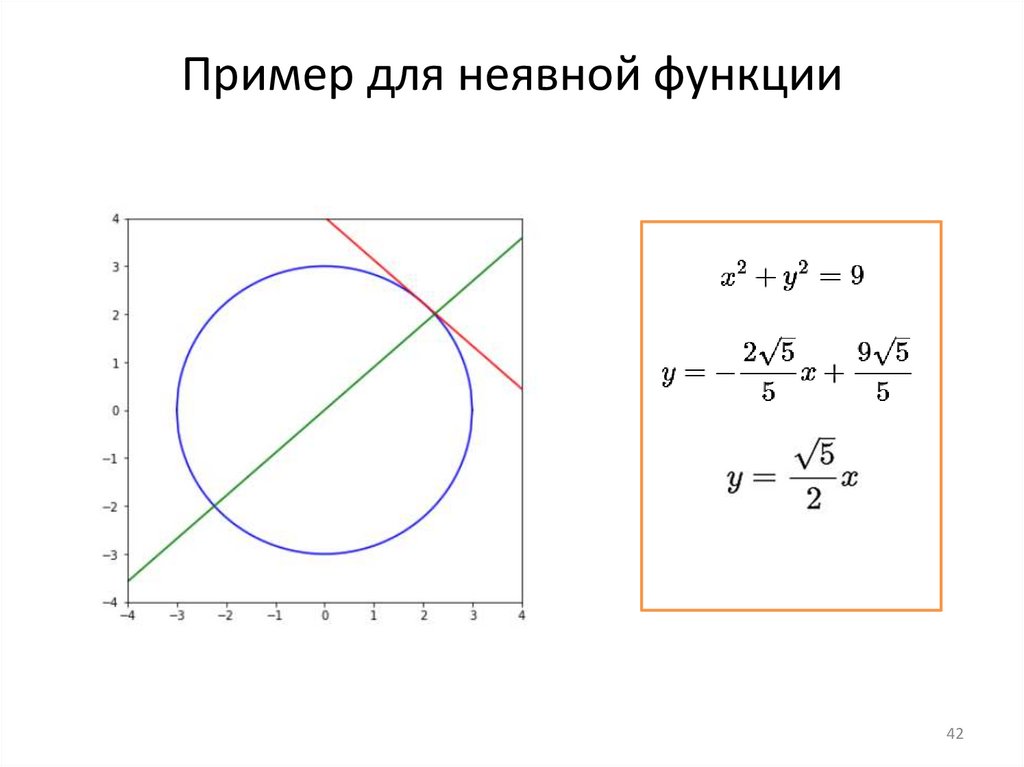
Пример для неявной функции
40

41.

Пример для неявной функции
41

42.

Пример для неявной функции
42

43.

Пример для функции, заданной параметрически
43

44.

Пример для функции, заданной параметрически
?
44

45.

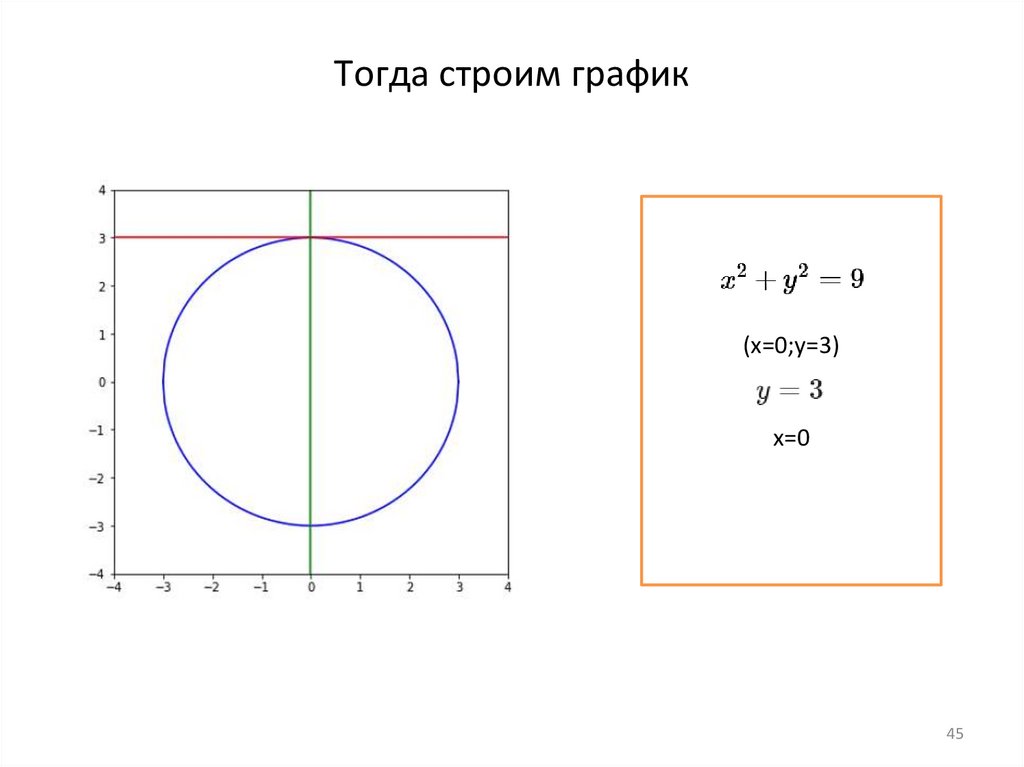
Тогда строим график
(x=0;y=3)
х=0
45

46.

Ваши вопросы:
Спасибо!
46