Похожие презентации:
Определенный интеграл
1.
§23. Определенный интегралп.1. Условия существования
определенного интеграла.
Теорема 1. (Необходимое условие
интегрирования)
Если функция
интегрируема на
отрезке
, то она ограничена на этом
отрезке.
2.
Доказательство (методом от противного).Пусть функция
отрезке [ a ; b ] .
не ограничена на
a x 0 x1 ... x i 1 x i ... x n 1 x n b
функция y f ( x ) не ограничена хотя бы
на одном отрезке [ x i 1 ; x i ].
z i [ x i 1 ; x i ], что произведение f ( z i ) x i
будет сколь угодно
большим.
3.
yy f ( x)
O
a
xi 1 zi
xi
b
x
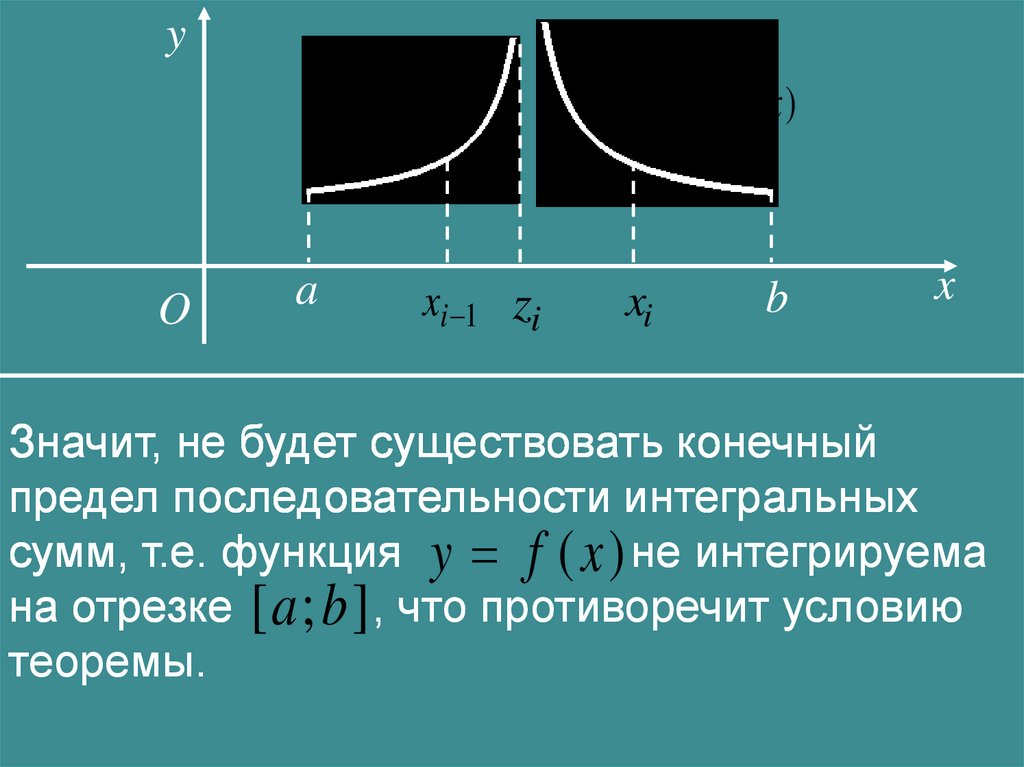
Значит, не будет существовать конечный
предел последовательности интегральных
сумм, т.е. функция y f ( x ) не интегрируема
на отрезке [ a ; b ] , что противоречит условию
теоремы.
4.
Замечание. Необходимое условие не являетсядостаточным.
Пример. Функция Дирихле
0, x иррациональное число,
D ( x)
1, x рациональное число;
является ограниченной на любом
отрезке [ a ; b ] , но не интегрируемой.
5.
D ( x) 1x [a; b]
a x 0 x1 ... x i 1 x i ... x n 1 x n b
z i [ x i 1 ; x i ] иррациональное число i 1, n :
n
S n D ( z i ) xi 0
i 1
z i [ x i 1 ; x i ] рациональное число i 1, n :
n
S n D ( z i ) xi b a
1
i 1
6.
lim S n не существуетn
функция D ( x ) не интегрируема на
отрезке [ a ; b ] .
7.
п.2. Интеграл с переменным верхнимпределом.
Если функция y f ( x ) интегрируема на
отрезке [ a ; b ] , то она интегрируема на любом
отрезке [ a ; x ] [ a ; b ] , т.е. существует
x
f (t )dt.
a
8.
x [ a ; b ] поставим в соответствие число,равное
x
f
(
t
)
dt
.
a
Таким образом, на [ a ; b ] будет определена
функция
x
( x ) f (t ) dt
a
─ интеграл с переменным верхним пределом.
9.
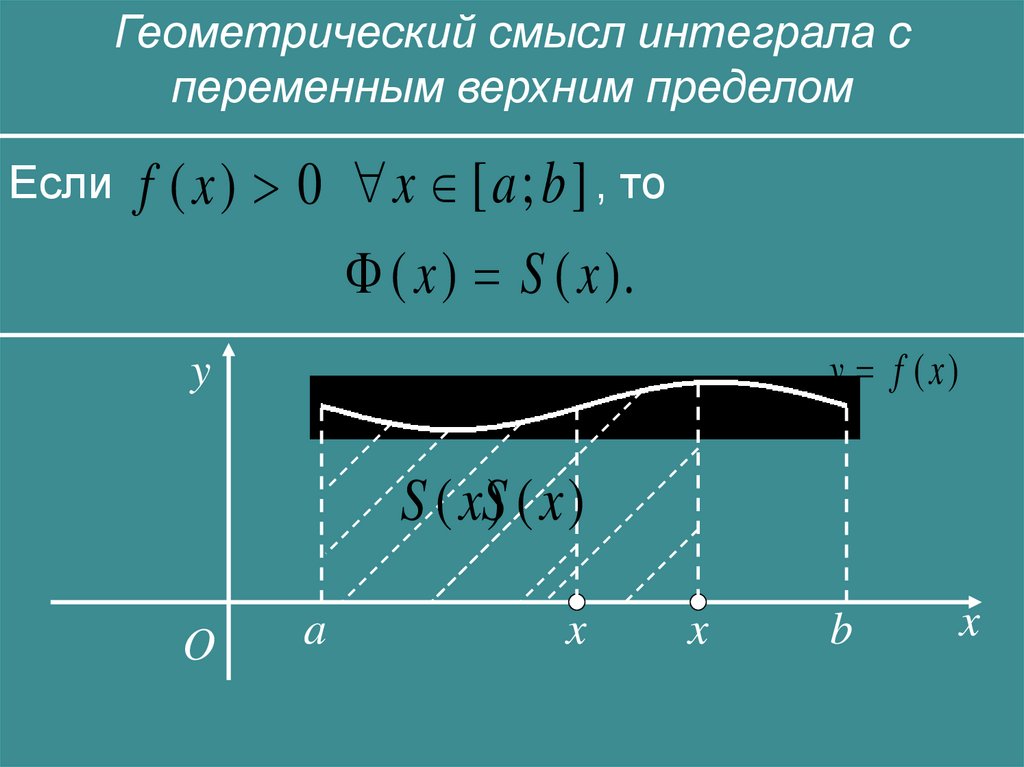
Геометрический смысл интеграла спеременным верхним пределом
Если f ( x ) 0 x [ a ; b ] , то
( x ) S ( x ).
y f ( x)
y
S ( xS) ( x )
O
a
x
x
b
x
10.
Теорема 2. (Основное свойство интеграла спеременным верхним пределом)
Если функция y f ( x ) непрерывна на
отрезке [ a ; b ], то функция
x
( x ) f (t ) dt
a
является дифференцируемой на [ a ; b ],причем
'
' ( x ) f (t ) dt f ( x ).
a
x
11.
Замечание. Функцияx
( x ) f (t ) dt
a
является первообразной
для функции y f ( x ) на ( a ; b ] .
12.
Доказательство теоремы 2.( x x) ( x)
' ( x ) lim
lim
x 0
x 0 x
x
x x
x
a
a
x
x x
x
a
x
a
f (t )dt f (t )dt
f (t ) dt
f (t )dt f (t ) dt
13.
x xf
(
t
)
dt
f
(
c
)
x
,
x
Теорема 1 §14
c [ x; x x ]
14.
f (c ) xlim
lim
f ( x)
x 0 x
x 0
x
lim c x
x 0
c [ x; x x ]
'(x) f (x)
15.
п.3. Вычисление определенногоинтеграла.
Теорема 3.
Пусть
функция f ( x ) непрерывна на отрезке [ a ; b ] ;
F ( x ) ─ одна из первообразных функции f ( x ) .
Тогда
справедлива формула Ньютона–Лейбница
b
a
b
f ( x ) dx F ( x ) a F (b ) F ( a ).
16.
Доказательство.F ( x ) ─ первообразная функции f ( x )
x
( x ) f (t ) dt ─ первообразная функции f ( x )
a
Замечание
( x ) F ( x ) C , C const
Теорема 1 §12
17.
xf (t )dt F ( x) C
a
x a
a
f (t )dt F (a ) C
a
0 F (a ) C
C F (a )
18.
xf (t )dt F ( x) C
a
x b
b
C F (a )
f (t )dt F (b) F (a )
a
19.
Пример.0
dx
x 2 22xx 2
1
0
dx
1 ( x 1)
2
1
0
arctg ( x 1) 1
arctg 0 arctg ( 1)
4
20.
Теорема 4. (О замене переменной вопределенном интеграле)
Пусть
функция f ( x ) непрерывна на отрезке [ a ; b ] ;
функция x (t ) имеет непрерывную
производную на отрезке [ ; ];
E ( ) [ a ; b ]; a ( ); b ( ).
Тогда справедлива формула
b
a
f
(
x
)
dx
f
(
(
t
))
'
(
t
)
dt
.
x ( t )
21.
Доказательство.b
Теорема 3
f ( x)dx F (b) F (a )
a
F ( x ) ─ первообразная функции f ( x )
22.
G ( t ) F ( ( t ))G ' ( t ) F ' ( ( t )) ' ( t ) f ( ( t )) ' ( t )
Теорема 4 §8
F ( x ) ─ первообразная функции f ( x )
G (t ) ─ первообразная функции f ( ( t )) ' ( t )
23.
Теорема 3f
(
(
t
))
'
(
t
)
dt
G
(
)
G
(
)
F ( ( )) F ( ( )) F ( b ) F ( a )
24.
Теорема 5.Пусть
функции u u ( x ) и v v ( x ) имеют
непрерывные производные на отрезке [ a ; b ].
Тогда справедлива формула
b
a
b
udv uv a
b
vdu.
a
25.
Доказательство.( uv )' u ' v uv '
uv ─ первообразная функции u ' v uv '
Теорема 3
b
a
b
u ' ( x )v ( x ) u ( x )v ' ( x ) dx u ( x )v ( x ) a
du u ' ( x ) dx dv v ' ( x ) dx
26.
bb
a
a
vdu
b
a
b
udv uv a
b
udv uv a
b
vdu
a
27.
Пример.uu
xx
1
xx
1
dv e dx
x1
x
x
xe
dx
xe
e
dx
0
du
dx
0
0
0
v e
x
e 0 e
1
x1
0
e ( e 1) 1



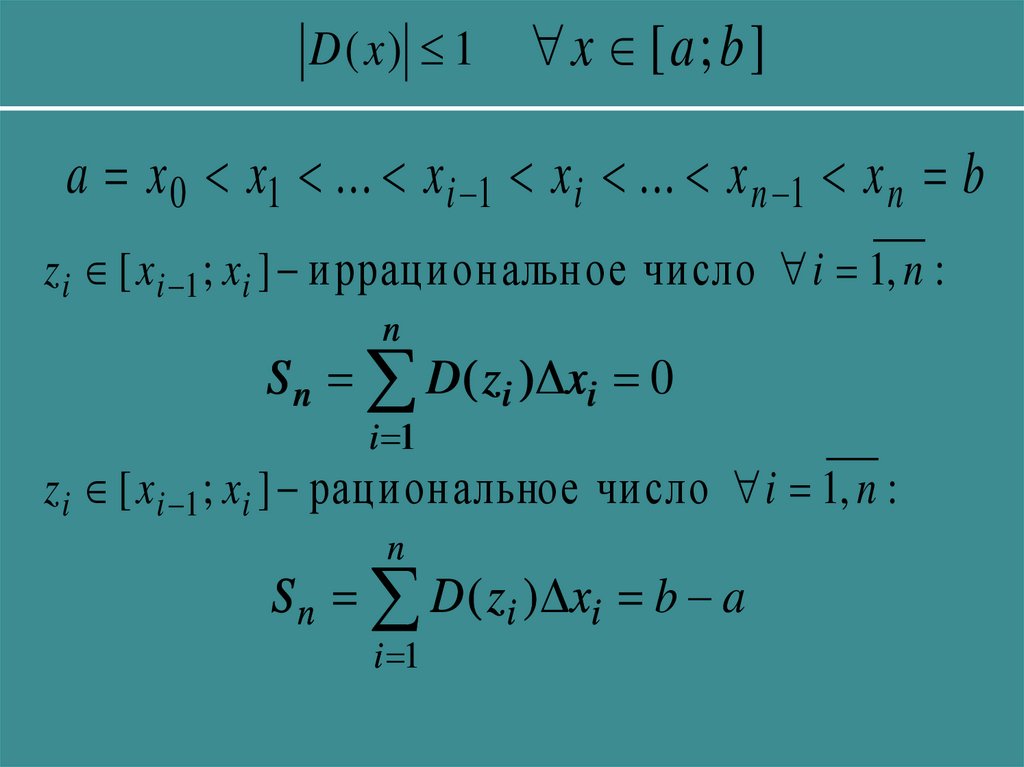







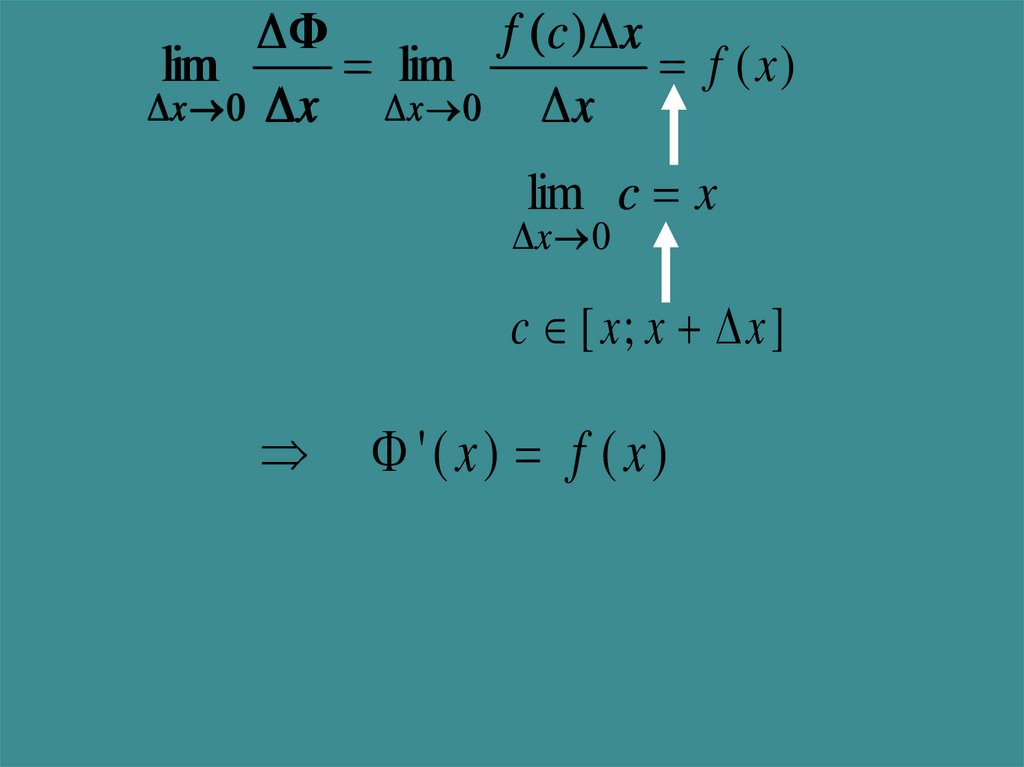


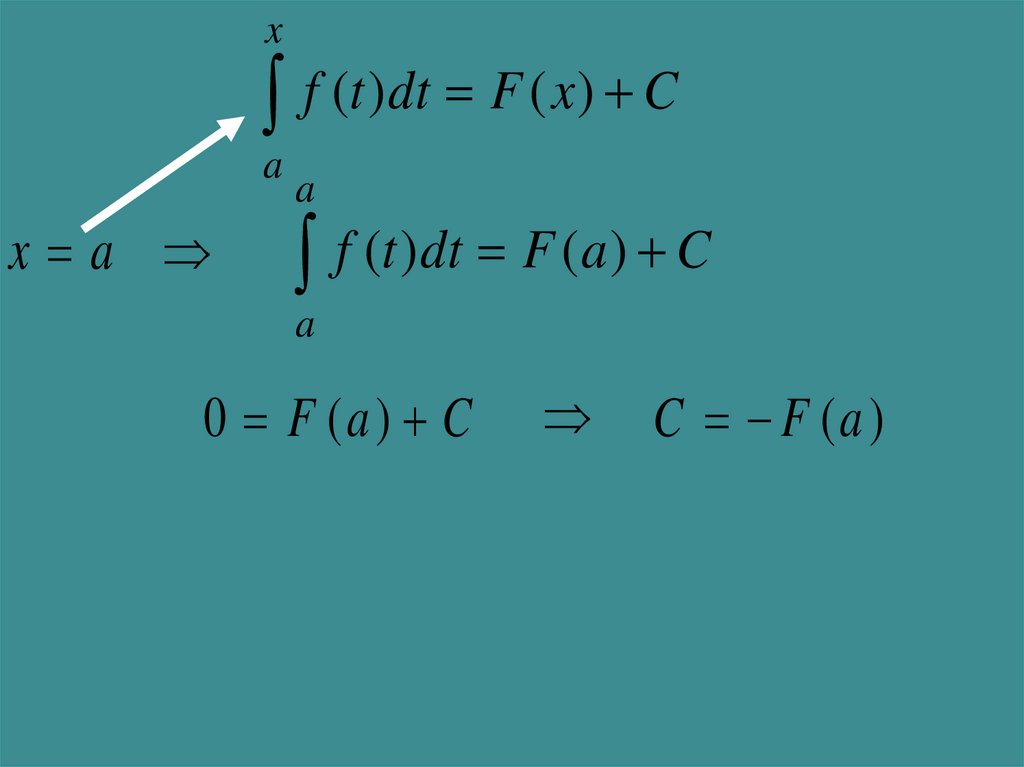
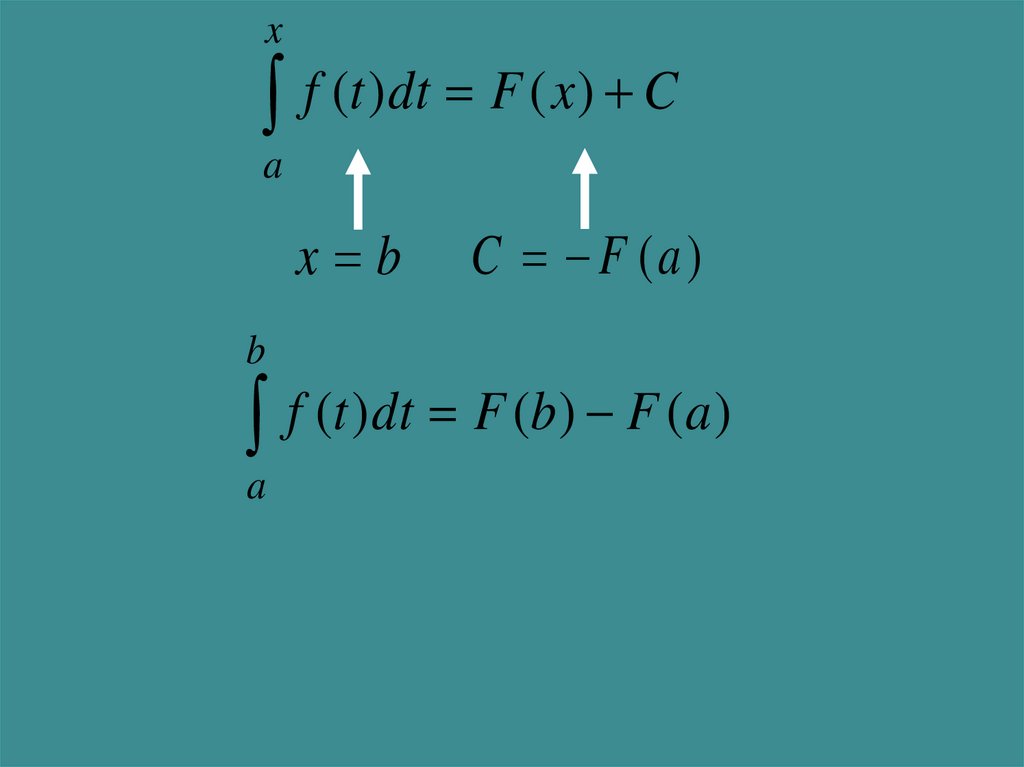
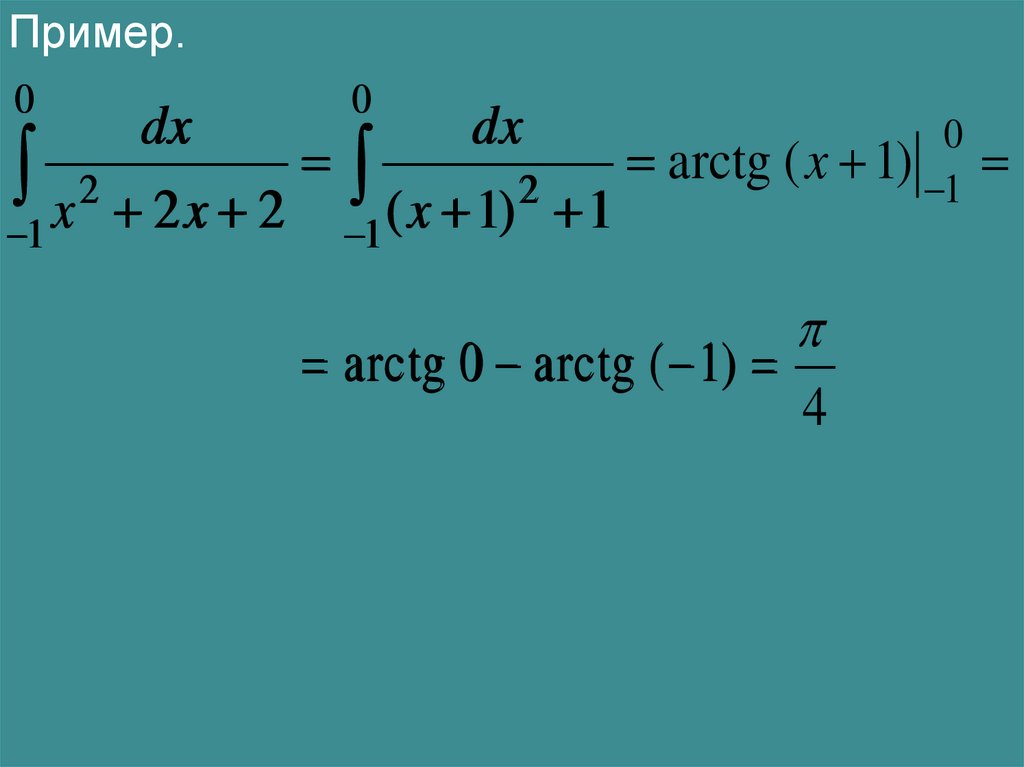



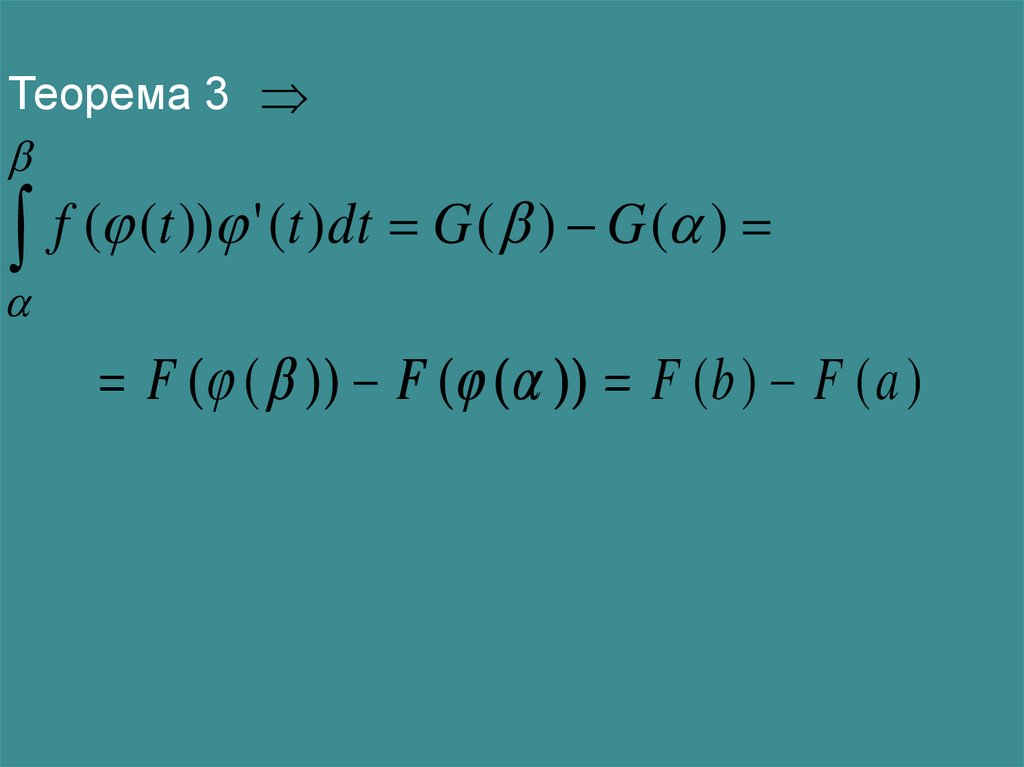


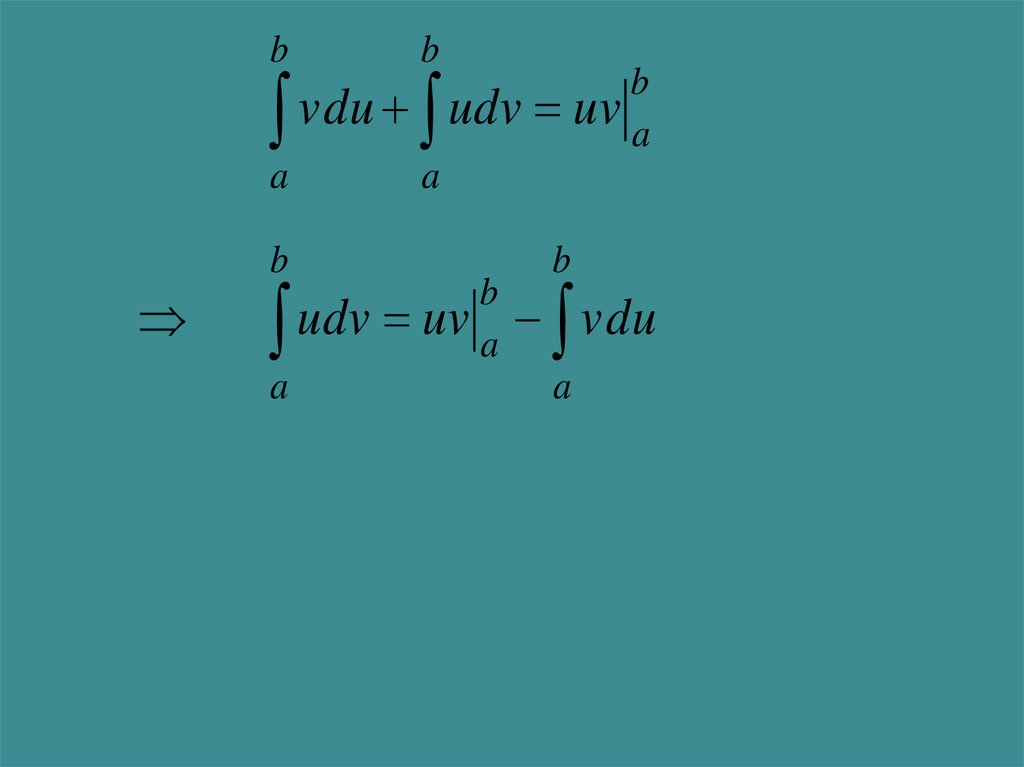
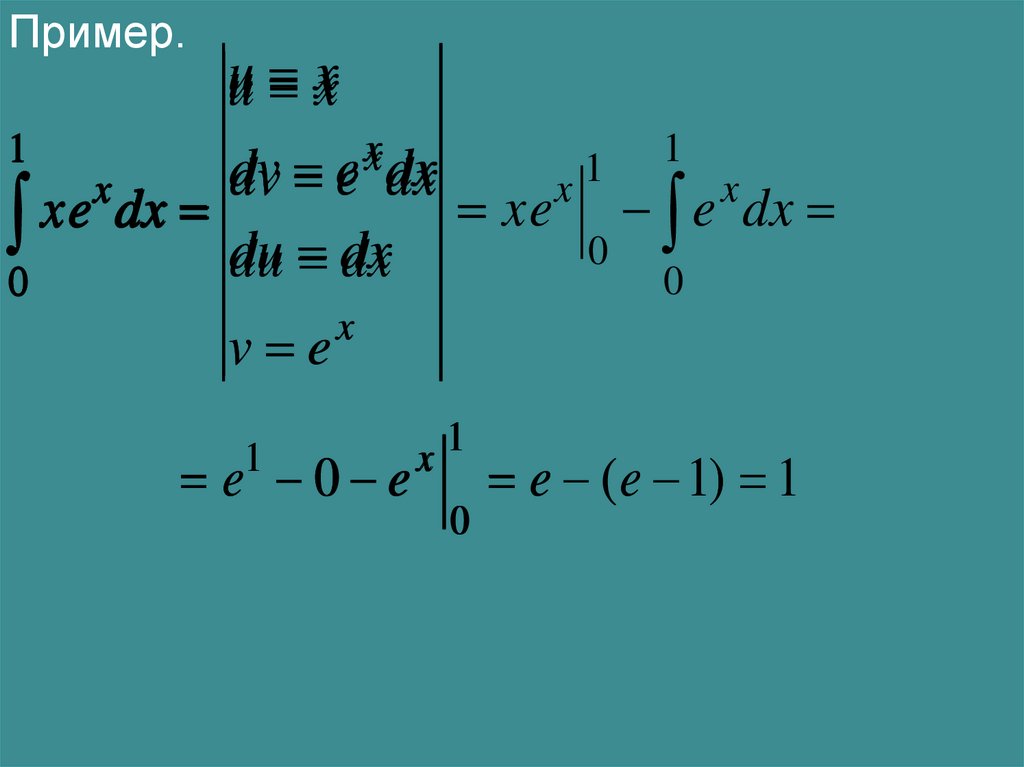
 Математика
Математика








