Похожие презентации:
Определённый интеграл
1.
Лекция 8Определённый интеграл.
1. Задача о вычислении площади криволинейной
трапеции.
2. Определённый интеграл как предел
интегральной суммы.
3. Свойства определённого интеграла.
2.
1. Задача о вычислении площади криволинейнойтрапеции.
Пусть f(x) - непрерывная на [ a, b ] функция.
Задача – вычислить площадь криволинейной
трапеции.
Для её решения разобьём криволинейную
трапецию на части точками деления:
a x0 x1 x2 ... xn b
3.
yx1 x1 x0 ;
y=f(x)
x2 x2 x1 ;
ci
a x1 x2 xi-1 xi b
S n fс
1
x
1
......................
x i x i x i 1 ;
ci [ xi 1 , xi ]
x
... f с
n
x
n
n
f с x
i 1
i
i
4.
Площадь криволинейной трапеции будет равнаприближённо сумме площадей прямоугольников:
S Sn
Обозначим max xi - наибольшую из длин
отрезков разбиения и рассмотрим такие разбиения
отрезка [a,b], при которых max xi 0 .
5.
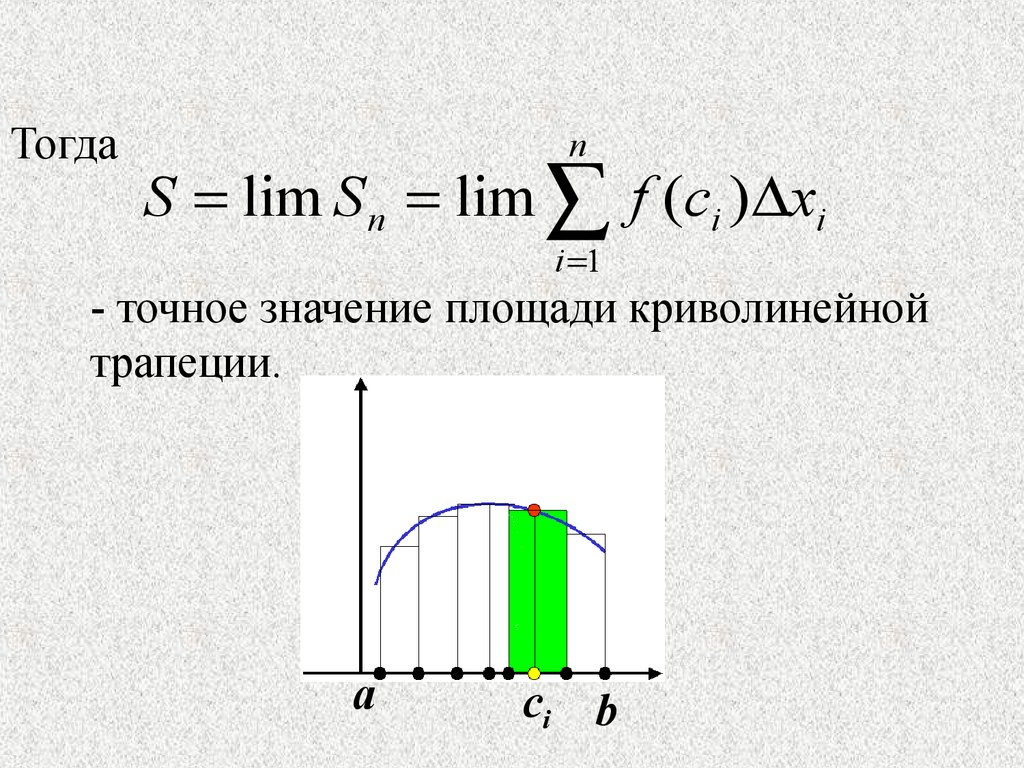
Тогдаn
S lim S n lim f (ci ) xi
i 1
- точное значение площади криволинейной
трапеции.
a
ci b
6.
2.Определённый интеграл как предел
интегральной суммы.
Построенные выше суммы вида
n
S n f (ci ) xi
i 1
называются интегральными суммами для
функции f(x) на отрезке [a,b].
7.
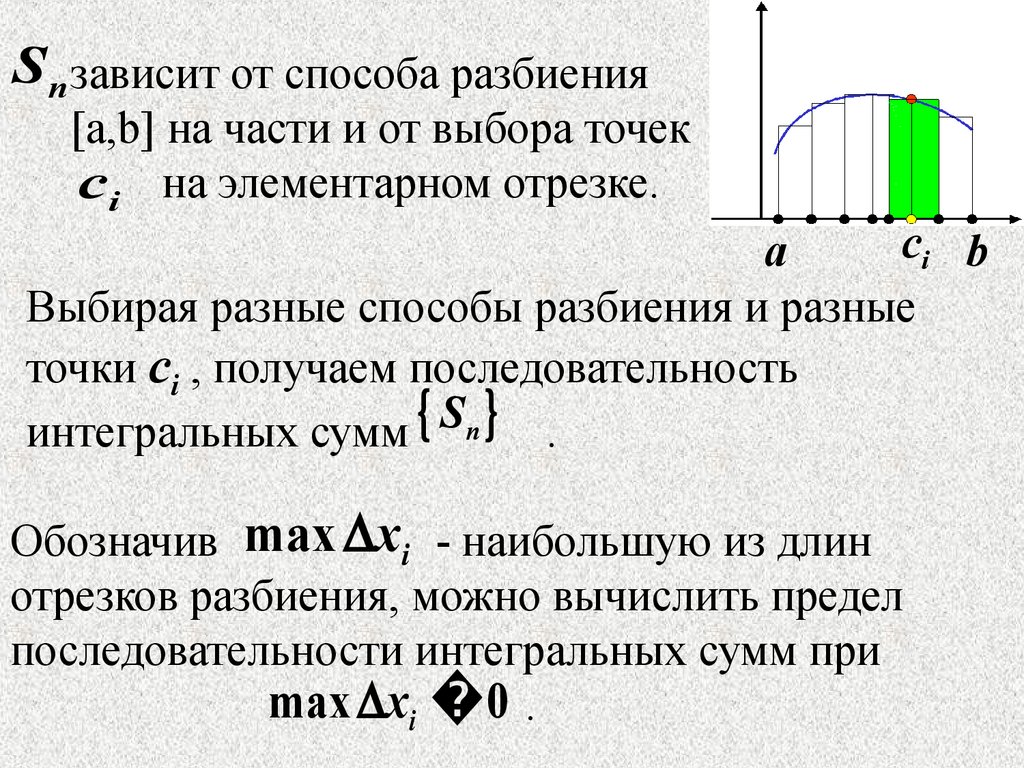
S n зависит от способа разбиения[a,b] на части и от выбора точек
ci на элементарном отрезке.
ci b
a
Выбирая разные способы разбиения и разные
точки ci , получаем последовательность
интегральных сумм S n .
Обозначив max xi - наибольшую из длин
отрезков разбиения, можно вычислить предел
последовательности интегральных сумм при
max xi 0 .
8.
Определенным интегралом от f (x) наотрезке [ a, b] называется число, равное пределу
последовательности её интегральных сумм
b
f ( x )dx
a
n
lim
max xi 0
f c x
i 1
i
а - нижний предел,
b - верхний предел интегрирования.
i
9.
ЕслиЕсли существует
существует
b
то
функция
то
функция
f
(
x
)
dx
f (x)
a
называется
называется интегрируемой
интегрируемой на
на отрезке
отрезке
[ a, b]
10.
Геометрический смысл определенногоинтеграла.
y
f(x)>0
b
a
a
b
x
f ( x)dx S
11.
Теорема существования :Т
Если
f ( x)
непрерывна на [a,b],
то
f ( x)
интегрируема на [a,b].
12.
Замечания.a
f ( x)dx 0
1.
a
b
2.
a
a
f ( x)dx f ( x)dx
b
13.
3. Свойства определенного интеграла.1. Независимость величины интеграла от
обозначения переменной интегрирования.
b
a
b
f ( x)dx f (t )dt
a
2. Линейность.
b
b
b
Af ( x) Bf ( x) dx A f ( x)dx B f ( x)dx
1
a
2
1
a
2
a
14.
3. Аддитивность (разбиение на сумму интеграловпо частям отрезка).
b
c
b
a
a
c
f ( x )dx
f ( x )dx
f ( x )dx
( между а и в можно вставить любое число с )
15.
4. Сохранение знака интеграла .Т
Если
1) f ( x )
интегрируема на [a,b],
2) f ( x ) 0, x [a , b],
то
b
f ( x )dx 0
a
16.
5. Интегрирование неравенств.Т
Если
1) f ( x ), g( x )
интегрируемы на [a,b],
2) f ( x ) g( x ), x [a , b],
то
b
b
a
a
f
(
x
)
dx
g
(
x
)
dx
17.
6. Теорема об оценке интеграла.Т
Если
1) f ( x )
2) m , M
интегрируема на [a,b],
- наименьшее и наибольшее
значения функции на [a,b],
то
b
m b a
f ( x )dx M b a
a
18.
7. Теорема о среднем.Т
Если
f ( x)
непрерывна на [a,b],
то c a , b
b
такое что
f
(
x
)
dx
b
a
f
c
a
19.
Доказательство:1
m
b a
b
b
Из теоремы об оценке
f ( x )dx M
a
1
f ( x )dx A,
b a a
m A M
f ( x ) непрерывна принимает все
промежуточные значения между m и M .
Следовательно, на отрезке [a,b] существует
точка с в которой f(c)=A:
b
f
(
x
)
dx
b
a
f
c
.
a
20.
Замечание.Средним значением функции f(x) на отрезке
[a,b] называется число, определяемое по
формуле:
b
f (c )
f ( x ) dx
a
(b a )


















 Математика
Математика








