Определенный интеграл

1. Определенный интеграл

Работу подготовила
Коваленко Ирина Анатольевна,
учитель математики школы №3
города Стародуба Брянской области
Задачи, приводящие к понятию
определенного интеграла

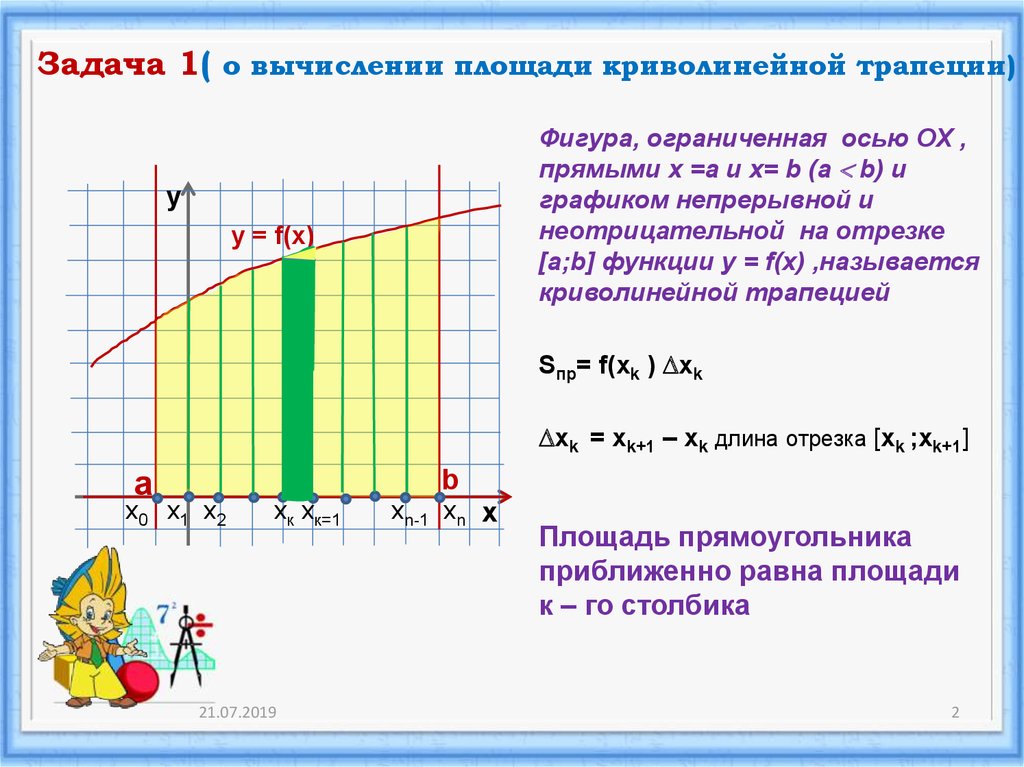
2. Задача 1( о вычислении площади криволинейной трапеции)

Фигура, ограниченная осью ОХ ,
прямыми х =а и х= b (а b) и
графиком непрерывной и
неотрицательной на отрезке
[a;b] функции у = f(x) ,называется
криволинейной трапецией
у
у = f(x)
Sпр= f(xk ) xk
xk = xk+1 – xk длина отрезка [xk ;xk+1]
а
b
x0 х1 х2
хк хк=1
21.07.2019
хn-1 хn х
Площадь прямоугольника
приближенно равна площади
к – го столбика
2

3.

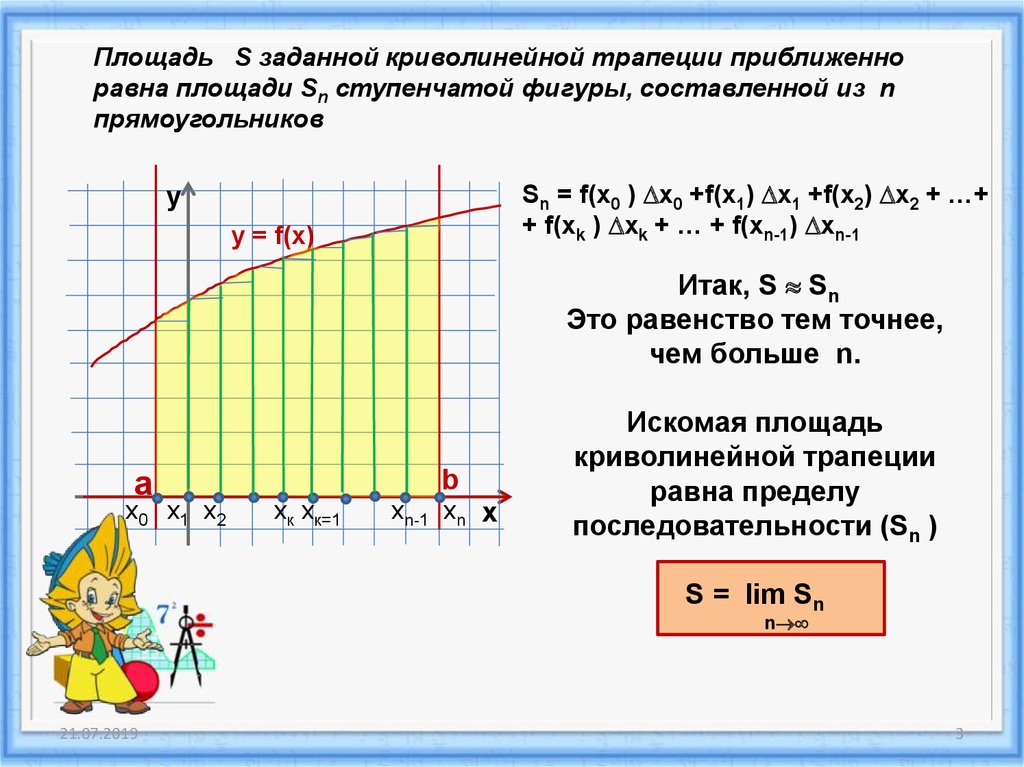
Площадь S заданной криволинейной трапеции приближенно
равна площади Sn ступенчатой фигуры, составленной из n
прямоугольников
Sn = f(x0 ) x0 +f(x1) x1 +f(x2) x2 + …+
+ f(xk ) xk + … + f(xn-1) xn-1
у
у = f(x)
Итак, S Sn
Это равенство тем точнее,
чем больше n.
а
x0 х1 х2
b
хк хк=1
хn-1 хn х
Искомая площадь
криволинейной трапеции
равна пределу
последовательности (Sn )
S = lim Sn
n
21.07.2019
3

4.

Математическое описание модели, построенной для
функции у = f(x) , определенной на отрезке [a;b]:
1) разбивают отрезок на n равных частей;
2) составляют сумму Sn = f(x0 ) x0 +f(x1) x1 +f(x2) x2 + …+
+ f(xk ) xk + … + f(xn-1) xn-1
3) вычисляют lim Sn
n
lim Sn называют определенным интегралом от функции у = f(x)
n
по отрезку [a;b].
Обозначают :
21.07.2019
4

5.

Исаак Ньютон (1643 – 1727)
– английский физик
Готфрид Лейбниц(1646 – 1716)
–немецкий философ,
математик и физик
= F(x) |ba = F(b) – F (a)
21.07.2019
5